Bộ 12 đề thi học kì 2 Toán 7 Cánh Diều cấu trúc mới có đáp án - Đề 10
6 câu hỏi
Quan sát biểu đồ sau:
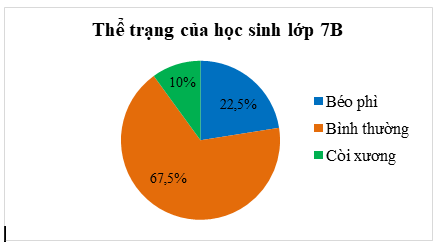
a) Tỉ số phần trăm số học sinh bị còi xương và học sinh béo phì là bao nhiêu?
b) Tính số học sinh bị còi xương và số học sinh béo phì, biết sĩ số lớp là học sinh.
c) Trong tổng số học sinh bị còi xương và học sinh béo phì, chọn ngẫu nhiên một học sinh. Tính xác suất để học sinh được chọn bị còi xương.
Trong hộp gỗ gồm 6 thẻ gỗ cùng loại, được đánh số \(12;13;14;15;16;17\) rút ngẫu nhiên một thẻ.
a) Viết tập hợp \(A\) gồm các kết quả có thể xảy ra đối với số xuất hiện trên quả bóng được rút ra.
b) Tính xác suất của biến cố \(B\): “Thẻ rút được là ước của 24”.
c) Tính xác suất của biến cố \(C\): “Thẻ rút được chia 3 dư 2”.
Trong một ngày hè, buổi sáng nhiệt độ là \(x^\circ C\), buổi trưa tăng thêm \(y^\circ C\). Buổi chiều lúc mặt trời lặn nhiệt độ lại giảm đi \(z^\circ C\) so với ban trưa.
a) Viết biểu thức đại số biểu thị nhiệt độ mặt trời theo \(x,y,z\).
b) Tính giá trị biểu thức đại số khi \(x = 30^\circ C,y = 6^\circ C,z = 10^\circ C\).
Cho hai đa thức: \(M\left( x \right) = 2{x^4} - 3{x^3} - x + 7{x^3} - 5x + 1\);
\(N\left( x \right) = - 2{x^3} + {x^2} + 3{x^4} + 5x - 2{x^4} - 6 + x\).
a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm dần của biến.
b) Xác định bậc và hệ số cao nhất của hai đa thức \(N\left( x \right)\).
c) Tính \(8M\left( 1 \right) + N\left( { - 1} \right)\).
d) Tìm đa thức \(Q\left( x \right)\) sao cho \(Q\left( x \right) = M\left( x \right) + N\left( x \right)\).
Tìm \(x\) để \(Q\left( x \right) = \left( {3x - 1} \right)\left( {{x^3} + {x^2}} \right) + {x^2} + 4\).
5.1. Cho tam giác \(ABC\) có \(\widehat {BAC} = 60^\circ \). Tia phân giác của góc \(B\) cắt \(AC\) ở \(D\). Tia phân giác của góc \(C\) cắt \(AB\) ở \(E;\) \(BD\) và \(CE\) cắt nhau ở \(M.\) Hỏi số đo \(\widehat {EMD}\) bằng bao nhiêu độ?
5.2. Cho tam giác \[ABC\] cân tại \(A\). Lấy điểm \(D\) trên cạnh \(AC\), điểm \(E\) trên cạnh \(AC\) sao cho \(BD = CE\).
a) Chứng minh \(AD = AE\) và \(\Delta ABE = \Delta ACD\).
b) Chứng minh \[\Delta ABI = \Delta ACI\], từ đó suy ra \[AI\] là đường phân giác của góc \[BAC\].
c) Tìm vị trí của hai điểm \[D\] và \[E\] sao cho \[BD = DE = EC\]. Khi đó tìm vị trí của điểm \(I.\)
Một khu vui chơi bán \[100\] vé vui chơi trong ngày, các vé được ghi một trong các số \[1,2,3,....,99,100\] (hai vé khác nhau thì ghi hai số khác nhau). Nam mua ngẫu nhiên một vé. Tính xác suất “Số ghi trên vé của Nam là số có tổng các chữ số bằng \[9\]”.








