Bộ 12 đề thi học kì 2 Toán 7 Cánh Diều cấu trúc mới có đáp án - Đề 05
30 câu hỏi
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Thực hiện phong trào kế hoạch nhỏ của Đội phát động, sau một tuần lớp trưởng lớp 7A đã vẽ được biểu đồ thống kê chai nhựa cả lớp thu gom được như sau:
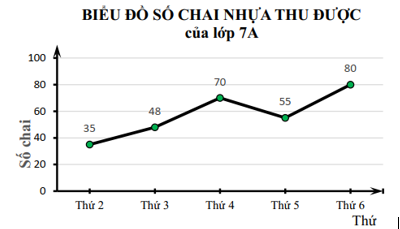
Số lượng chai nhựa thu được nhiều nhất trong một ngày là
\(100.\)
\(80.\)
\(288.\)
\(70.\)
Gieo một con xúc xắc cân đối. Xét các biến cố sau, biến cố nào là biến cố chắc chắn?
“Mặt xuất hiện có số chấn nhỏ hơn 7”.
“Mặt xuất hiện có số chấm chia hết cho 7”.
“Mặt xuất hiện có số chấm lớn hơn 4”.
“Mặt xuất hiện có số chấm nhỏ hơn 2”.
Biểu thức đại số biểu thị nửa tổng của \(x\) và \(y\) là
\(x + y.\)
\(\frac{x}{2} + y.\)
\(\frac{{x + y}}{2}.\)
\(x + \frac{y}{2}.\)
Biểu thức biểu thị quãng đường Nam đi được trong \(x\) giờ với vận tốc là \(40{\rm{ km/h}}\) là
\(40x.\)
\(40 + x.\)
\(40:x.\)
\(\frac{x}{{40}}.\)
Kết quả của phép nhân hai đa thức \(\left( {2x - 3} \right)\left( {2x + 3} \right)\) là
\(4{x^2} + 12x + 9.\)
\(4{x^2} - 9.\)
\(2{x^2} - 3.\)
\(4{x^2} + 9.\)
Biết \(P\left( x \right) = 2{x^2} + 5\) và \(Q\left( x \right) = 3{x^2}\). Tổng của đa thức \(P\left( x \right) + Q\left( x \right)\) là
\(6{x^2} + 5.\)
\( - {x^2} + 5.\)
\(5{x^2} + 5.\)
\(5{x^2}.\)
Cho \(\Delta ABC\) có \(\widehat B = 70^\circ ,\widehat A = 50^\circ \). Khẳng định nào sau đây là đúng?
\(AB > BC > AC.\)
\(AC > AB > BC.\)
\(BC > AB > AC.\)
\(AC > BC > AB.\)
Cho \(\Delta MNP\) và \(\Delta HIK\) có \(MN = HI,PM = HK\). Cần thêm điều kiện nào để hai tam giác trên bằng nhau theo trường hợp cạnh – cạnh – cạnh?
\(MP = IK.\)
\(NP = KI.\)
\(NP = HI.\)
\(MN = HK.\)
Cho \(\Delta ABC\) có \(\widehat A = 70^\circ ,\widehat B = 55^\circ \). Ta có:
\(\Delta ABC\) cân tại \(A.\)
\(\Delta ABC\) cân tại \(B.\)
\(\Delta ABC\) cân tại \(C.\)
\(\Delta ABC\) vuông.
Trong \(\Delta ABC\) có trung tuyến \(AM\) và trọng tâm \(G\). Kết quả nào dưới đây sai?
\(AG = \frac{2}{3}AM.\)
\(GM = \frac{1}{2}GA.\)
\(GA = \frac{1}{3}GM.\)
\(MB = MC.\)
Cho \(\Delta ABC\) có \(I\) là giao điểm của ba đường phân giác trong \(\Delta ABC\). Khi đó, ta có:
\(AI\) vuông góc với \(BC.\)
\(I\) cách đều ba đỉnh của \(\Delta ABC\).
\(\Delta ABI\) cân ở \(I.\)
\(I\) cách đều ba cạnh của \(\Delta ABC\).
Vịnh Hạ Long là một trong bảy kì quan thiên nhiên của thế giới, giả sử 3 hòn núi đá tạo thành một tam giác, người ta muốn xây dựng một cột đèn để chiếu sáng cả ba hòn núi trên sao cho cột đèn cách đều ba điểm được đánh dấu trên hòn núi đá. Khi đó vị trí cột đèn sẽ nằm ở:
Trọng tâm của tam giác.
Trực tâm của tam giác.
Giao điểm của ba đường phân giác của tam giác.
Giao điểm của ba được trung trực của tam giác.
a) Biến cố “Thẻ rút được là số nguyên tố” là biến cố chắc chắn.
b) Biến cố “Thẻ rút được là ước của \(72\)” là biến cố ngẫu nhiên.
c) Xác suất của biến cố “Thẻ rút được là bội của \(2\)” là \(\frac{1}{2}.\)
d) Xác suất của biến cố “Thẻ rút được là số chia \(3\) dư \(2\)” là \(\frac{2}{3}\).
a) \(\Delta ABC = \Delta ACD\).
b) \(\Delta CBD\) cân tại \(B.\)
c) \(BC = DE.\)
d) \(BC = 6GM.\)
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Một hộp có \(25\) chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số \(1,2,3,4,...,25\). Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp, Tính xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số khi chia cho 4 và 5 đều có số dư là 1”.
(Kết quả ghi dưới dạng số thập phân)
Tính giá trị của biểu thức \(A = {x^{100}}{y^{100}} + {x^{99}}{y^{99}} + ... + {x^2}{y^2} + xy + 1\) tại \(x = - 1,y = 1\).
Cho đa thức \(h\left( x \right) = {x^3} + 3{x^2} + 5x + m\) (\(m\) là hệ số). Tìm giá trị của \(m\) để đa thức chia hết cho \(x + 1.\)
Cho \(\Delta ABC,\) \(\widehat B = \widehat C = 45^\circ \). Điểm \(E\) nằm trong tam giác sao cho \(\widehat {EAC} = \widehat {ECA} = 15^\circ \). Tính \(\widehat {BEA}\)?
a) Tính \(A\left( x \right) + B\left( x \right)\) và \(A\left( x \right) - B\left( x \right)\).
b) Tìm đa thức \(C\left( x \right)\) biết \(\left( {2x + 1} \right).C\left( x \right) = A\left( x \right)\).
c) Chứng minh rằng \(3A\left( x \right) - 2B\left( x \right) + 13{x^2} - 12x\) có giá trị không phụ thuộc vào \(x.\)
a) Chứng minh \(\Delta AHB = \Delta AHC.\)
b) Vẽ trung tuyến \(BM\) của \(\Delta ABC\). Trên tia đối của tia \(MB\) lấy điểm \(K\) sao cho \(MK = MB.\) Chứng minh \(\widehat {KAM} = \widehat {ABC}\).
c) Gọi \(O\) là giao điểm của \(AH\) và \(BM.\) Chứng minh rằng \(OK = 2OC.\)








