12 CÂU HỎI
Điểm nằm trên trục hoành thì sẽ có tung độ bằng bao nhiêu?
A.\( - 1.\)
B. \(1.\)
C. \(0.\)
D. \(2.\)
Trong mặt phẳng tọa độ \(Oxy\) như hình vẽ.
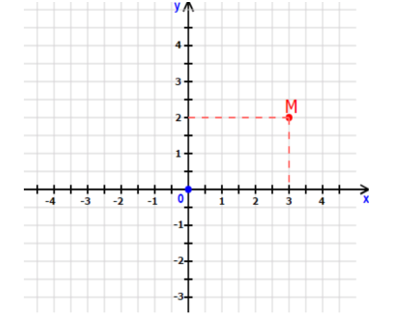
Tọa độ điểm \(M\) là
A.\(M\left( {3;2} \right).\)
B. \(M\left( {2;3} \right).\)
C. \(M\left( {3;0} \right).\)
D. \(M\left( {0;2} \right).\)
Biến đổi hàm số \(y = 2x + 3y + 1\) về hàm số bậc nhất ta được
A. \(y = - x - \frac{1}{2}.\)
B. \(3y = 2x + 1.\)
C. \(y = - x + 1.\)
D. \(y = 2x + 1.\)
Công thức biến đổi từ đơn vị độ \(F\) sang đơn vị độ \(C\) là \(C = \frac{5}{9}\left( {F - 32} \right)\). Hỏi nhiệt độ ở \(32^\circ F\) sẽ có giá trị bằng bao nhiêu độ \(C\)?
A. \(0.\)
B. \(62.\)
C. \(32.\)
D. \(\frac{5}{9}.\)
Phương trình nào dưới đây không phải phương trình bậc nhất một ẩn?
A.\(\frac{x}{5} + \frac{5}{3} = 0\).
B. \(1 + 2y = 0\).
C. \( - 3x + \frac{1}{2} = 0\).
D. \(2x - {x^2} = 0\).
Đưa phương trình \(2\left( {x + 2} \right) = 1 - 2x\) về dạng \(ax + b = 0\) là
A.\(4x + 3 = 0\).
B. \( - 2x + 1 = 0\).
C. \(4x + 5 = 0\).
D. \(2x + 4 = 0\).
Một xe tải và một xe con cùng khởi hành từ tỉnh \(A\) đến tỉnh \(B\). Xe tải đi với vận tốc \(30{\rm{ km/h,}}\)xe con đi với vận tốc \({\rm{45 km/h}}\). Nếu gọi quãng đường \(AB\) là \(x{\rm{ }}\left( {{\rm{km}}} \right)\) với \(x > 0\) thì thời gian xe tải đi từ \(A\) đến \(B\) là
A.\(30x\) giờ.
B. \(\frac{x}{{30}}\) giờ.
C. \(40x\) giờ.
D. \(\frac{x}{{40}}\) giờ.
Một cảnh sát giao thông đang đứng và bắn tốc độ các phương tiện giao thông tham gia trên đoạn đường có biển báo cho phép là \(80{\rm{ }}\left( {{\rm{km/h}}} \right)\). Theo luật giao thông thì vận tốc cho phép các phương tiện giao thông không vượt quá biển báo là \(x{\rm{ }}\left( {{\rm{km/h}}} \right)\). Một ô tô tham gia đi với vận tốc nào sau đây sẽ bị phạt \(\left( {{\rm{km/h}}} \right)\)
A. \(80 + x.\)
B. \(80 - x.\)
C. trên \(80 + x.\)
D. dưới \(80 - x.\)
Cho tam giác \(ABC\) có \(DE\parallel BC\). Khẳng định nào sau đây là sai?
A.\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\) suy ra \(DE\parallel BC.\)
B. \(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\) suy ra \(DE\parallel BC.\)
C.\(\frac{{BD}}{{AB}} = \frac{{EC}}{{AC}}\) suy ra \(DE\parallel BC.\)
D. \(\frac{{AD}}{{AB}} = \frac{{AE}}{{EC}}\) suy ra \(DE\parallel BC.\)
Cho hình vẽ, biết \(ON\parallel MP\).
Khi đó độ dài \(OM\) bằng
A.\(2{\rm{ cm}}{\rm{.}}\)
B. \({\rm{4 cm}}{\rm{.}}\)
C. \({\rm{6 cm}}{\rm{.}}\)
D. \({\rm{4,5 cm}}{\rm{.}}\)
Cho \(\Delta ABC\) có \(AB = 4{\rm{ cm;}}\)\(AC = 9{\rm{ cm}}{\rm{.}}\) Gọi \(AD\) là tia phân giác của \(\widehat {BAC}\). Tỉ số \(\frac{{CD}}{{BD}}\) bằng
A.\(\frac{4}{9}.\)
B. \(\frac{9}{4}.\)
C. \(\frac{4}{5}.\)
D. \(\frac{5}{4}.\)
Cho tam giác \(ABC\) có \(I,K\) lần lượt là trung điểm của \(AB,AC\). Biết \(BC = 8{\rm{ cm}}\). Độ dài \(IK\) là
A.\(4{\rm{ cm}}{\rm{.}}\)
B. \({\rm{16 cm}}{\rm{.}}\)
C. \({\rm{2 cm}}{\rm{.}}\)
D. \({\rm{12 cm}}{\rm{.}}\)
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải