12 câu hỏi
Biểu thức nào không phảilà đa thức trong các biểu thức sau?
\(2{x^2}y + 3 + xy\).
\(\frac{{x + y}}{2}\).
\(2 - \frac{{x + 1}}{{x - 1}}\).
\(x\left( {x + 2y} \right)\).
Đơn thức nào sau đây đồng dạng với đơn thức \( - 3{x^2}y\)?
\(3{x^2}yz\).
\(\frac{1}{2}xyx\).
\(x{y^2}\).
\( - 3{x^2}z\).
Tích của đa thức \[6xy\]và đa thức \[2{x^2} - 3y\]là đa thức
\[12{x^2}y + 18x{y^2}\].
\[12{x^3}y - 18x{y^2}\].
\[12{x^3}y + 18x{y^2}\].
\[12{x^2}y - 18x{y^2}\].
Hệ số của \[{x^4}\] trong đa thức \[A = \left( {{x^3} - 2{x^2} + x - 1} \right)\left( {5{x^3} - x} \right)\]là
\[4\].
\[ - 4\].
\[ - 6\].
\[6\].
Hằng đẳng thức bình phương của một hiệu là
\[{\left( {A + B} \right)^2} = {A^2} + 2\,.\,A\,.\,B + {B^2}\].
\[{\left( {A - B} \right)^2} = {A^2} - 2\,.\,A\,.\,B + {B^2}\].
\[{\left( {A - B} \right)^2} = {A^2} + 2\,.\,A\,.\,B + {B^2}\].
\[{\left( {A - B} \right)^2} = {A^2} - 2\,.\,A\,.\,B - {B^2}\].
Khai triển của \({x^3} - 27\) là
\(\left( {x - 3} \right)\left( {{x^2} - 3x + 9} \right)\).
\(\left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right)\).
\(\left( {x - 3} \right)\left( {{x^2} + 6x + 9} \right)\).
\(\left( {x - 3} \right)\left( {{x^2} - 6x + 9} \right)\).
Chiếc hộp bánh ít trong hình bên có dạng hình gì?

Hình lăng trụ đứng tam giác.
Hình chóp tam giác đều.
Hình chóp tứ giác đều.
Hình tam giác.
Cho hình chóp tam giác đều \[A.BCD\](như hình vẽ bên). Trung đoạn của hình chóp là đoạn thẳng
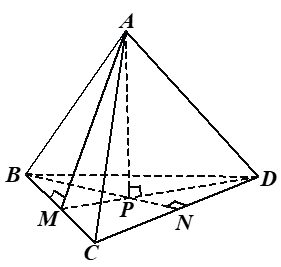
\[AM.\]
\[AC.\]
\[BN.\]
\[AP.\]
Hình chóp tam giác đều và hình chóp tứ giác đều có chung đặc điểm nào sau đây?
Đáy là tam giác đều.
Đáy là hình vuông.
Các cạnh bên bằng nhau.
Mặt bên là các tam giác đều.
Cho hình chóp tam giác đều \(S.ABC\) có đường cao \(SO\) (như hình vẽ). Các cạnh bên của hình chóptam giác đều là
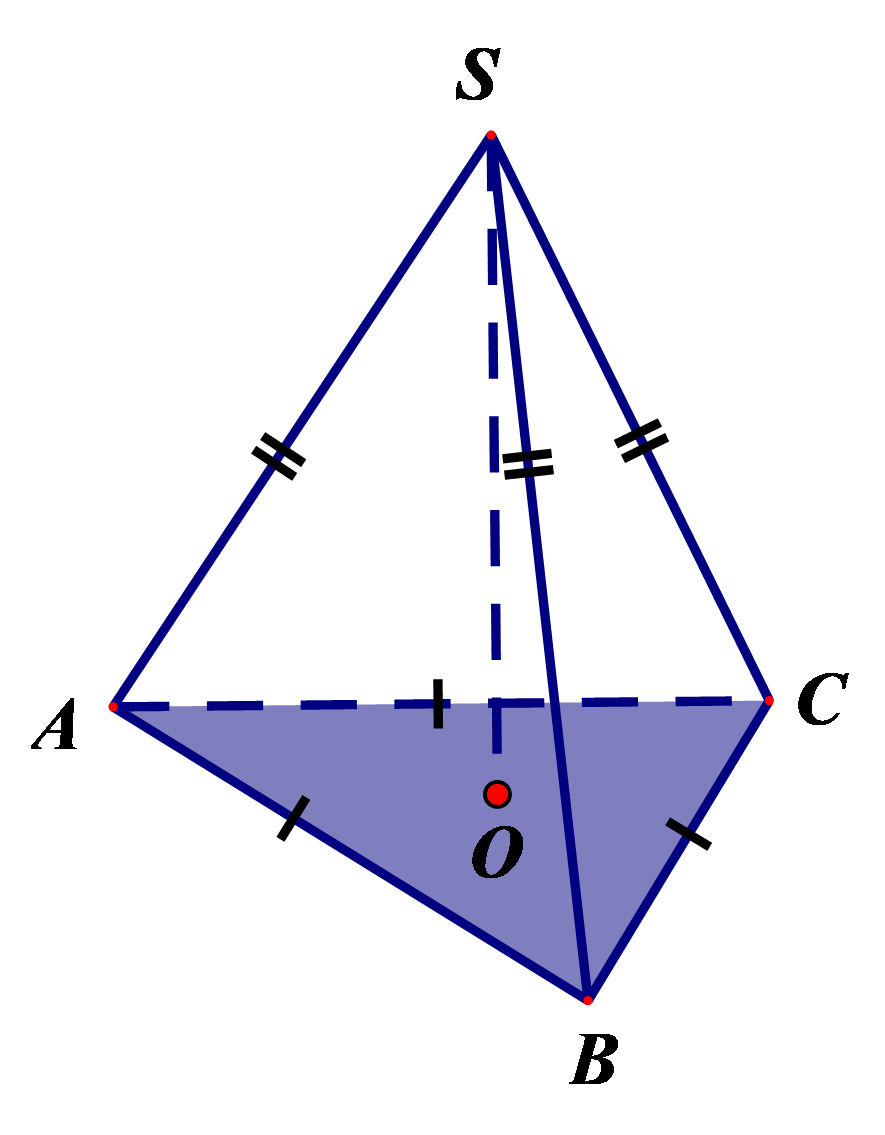
\(AB,\,\,BC,\,\,AC\).
\(SA,\,\,SB,\,\,SC,\,\,SO\).
\(SA,\,\,SB,\,\,SC\).
\(SAB,\,\,SBC,\,\,SAC\).
Cho tam giác \(ABC\) cân tại \(A\) có đường cao \(AH.\) Cho \(AH = 4\;\;{\rm{cm}},\,\,AB = 5\;\;{\rm{cm}}.\) Chu vi tam giác \(ABC\) bằng
\(16\;\;{\rm{cm}}\).
\(18\;\;{\rm{cm}}\).
\(12\;\;{\rm{cm}}\).
\(15\;\;{\rm{cm}}\).
Khẳng định nào sau đây là đúng?
Tứ giác có 4 đường chéo.
Tổng các góc của một tứ giác bằng .
Tồn tại một tứ giác có 1 góc tù và 3 góc vuông.
Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của tứ giác đó.
