12 câu hỏi
Cách viết nào sau đây biểu diễn một số hữu tỉ?
\(\frac{{6,5}}{{14}}.\)
\(\frac{3}{7}.\)
\(\frac{{21}}{0}.\)
\(\frac{{15}}{{0,2}}.\)
Cho hai số hữu tỉ \(a\) và \(b\) được biểu diễn trên trục số như sau:
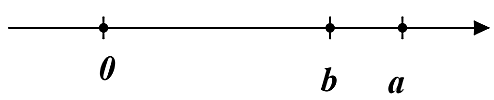
Khẳng định nào sau đây là đúng?
\(b > 0 > a.\)
\(b > a.\)
\(b < a < 0.\)
\(0 < b < a.\)
Kết quả của \({\left( { - \frac{1}{2}} \right)^3}\) là
\( - \frac{1}{8}.\)
\(\frac{1}{8}.\)
\(8.\)
\( - 8.\)
Thực hiện bỏ ngoặc của phép tính \( - \left( {a + 2} \right) + \left( {b - 2} \right)\) ta được
\(a + b - 4.\)
\(a - b - 4.\)
\( - a + b - 4.\)
\( - a - b - 4.\)
Trong các số sau, đâu là số vô tỉ?
\(\sqrt {121} .\)
\(0,\left( {12} \right).\)
\(0,010010001...\)
\( - 3,12\left( {345} \right).\)
Cho các số sau: \(\frac{1}{{81}};{\rm{ }} - {\rm{0,16; }}\frac{{ - 9}}{{ - 4}};{\rm{ }}{\left( { - 5} \right)^2}\). Số không có căn bậc hai là
\(\frac{1}{{81}}.\)
\( - 0,16.\)
\(\frac{{ - 9}}{{ - 4}}.\)
\({\left( { - 5} \right)^2}.\)
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có đường chéo
\(A'B'.\)
\(CC'.\)
\(B'C.\)
\(C'A.\)
Trong các hình sau đây, đâu là hình lăng trụ đứng tam giác?

Hình 1.
Hình 2.
Hình 3.
Hình 4.
Diện tích xung quanh của một hình lăng trụ đứng tứ giác có chu vi đáy là \(C\) và chiều cao \(h\) là
\({S_{xq}} = C.h.\)
\({S_{xq}} = \frac{1}{3}.C.h.\)
\({S_{xq}} = C + h.\)
\({S_{xq}} = 2.C.h.\)
Cho hình lăng trụ đứng tam giác \(ABC.A'B'C'\) có cạnh \(A'B' = 3{\rm{ cm,}}\) \(B'C' = 5{\rm{ cm,}}\) \(A'C' = 6{\rm{ cm,}}\) \[AA' = 7{\rm{ cm}}\]. Độ dài cạnh \[BC\] bằng
\[3{\rm{ cm}}{\rm{.}}\]
\[6{\rm{ cm}}{\rm{.}}\]
\[5{\rm{ cm}}{\rm{.}}\]
\[7{\rm{ cm}}{\rm{.}}\]
Cho hình bên. Góc kề bù với \(\widehat {aOb}\) là
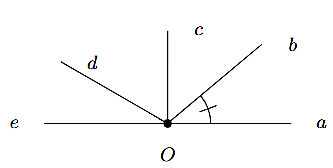
\(\widehat {aOc}.\)
\(\widehat {cOd}.\)
\(\widehat {eOb}.\)
\(\widehat {cOe}.\)
Quan sát hình vẽ. Góc đối đỉnh với \(\widehat {xEn}\) là
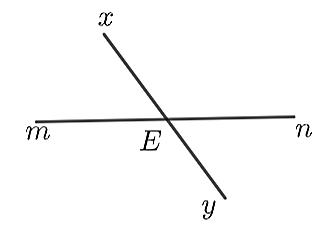
\(\widehat {mEy}.\)
\(\widehat {mEx}.\)
\(\widehat {nEy}.\)
\(\widehat {mEx}\) và \(\widehat {nEy}.\)
