Bộ 10 đề thi giữa kì 1 Toán 6 Cánh diều có đáp án - Đề 5
17 câu hỏi
Cách viết tập hợp nào sau đây là đúng?
\(A = 0;\,\,1;\,\,2;\,\,3\)
\(A = \left( {0;\,\,1;\,\,2;\,\,3} \right)\)
\(A = \left\{ {0;\,\,1;\,\,2;\,\,3} \right\}\)
\(A = \left[ {0;\,\,1;\,\,2;\,\,3} \right].\)
Cho tập hợp \[A = \left\{ {2;\;4;\;6} \right\}\] và \[B = \left\{ {1;\;2;\;3;\;4;\;5;\,6} \right\}\]. Chọn phương án đúng trong các phương án dưới đây.
\[1 \notin A\]
\[3 \in A\]
\[6 \notin B\]
\[5 \in A\].
Trong các tổng (hiệu) sau, tổng (hiệu) nào chia hết cho \(50\)?
\(5 + 50\)
\(100 + 150 + 450\)
\(20 + 150\)
\(250 - 10 + 50\).
Số La Mã liền sau số \(XXIX\) là số
\(XXX\)
\(XXXI\)
\(IXXX\)
\(XIXX\).
\(5\) là kết quả của phép tính nào dưới đây?
\(24:4 - {1^{123}}\)
\({5^3}:{5^2} + {2022^0}\)
\(6 - {(6 - 5)^2}\,.\,\,2\)
\(\left[ {\left( {15 - 3} \right):3 + {9^0}} \right]\,\,.\,\,2\).
Tập hợp các ước của \(15\) là
\(\left\{ {1;\,\,15} \right\}\)
\(\left\{ {3;\,\,5;\,\,15} \right\}\)
\(\left\{ {5;\,\,3} \right\}\)
\(\left\{ {1;\,\,3;\,\,5;\,\,15} \right\}\).
Nếu \[a\,\, \vdots \,\,3;\;\,\,b\,\, \vdots \,\,3;\;\,\,c\,\, \vdots \,\,3\] thì kết luận nào sau đây là đúng?
\[\left( {a + b + c} \right)\,\, \vdots \,\,3\]
\[\left( {a + b + c} \right)\,\, \vdots \,\,6\]
\[\left( {a + b + c} \right)\,\, \vdots \,\,9\]
\[\left( {a + b + c} \right)\,\, \vdots \,\,27\].
Số tự nhiên \[x\] lớn nhất thỏa mãn điều kiện \[13;{\rm{ }}61\] chia \[x\] dư \[1\] là
\[11\]
\[13\]
\[14\]
\[12\].
Khẳng định nào sau đây sai?
Tam giác đều có ba cạnh bằng nhau
Hình thoi có bốn góc bằng nhau
Lục giác đều có 6 cạnh bằng nhau
Hình vuông có bốn cạnh bằng nhau.
Gấp đôi một tờ giấy hình chữ nhật, rồi cắt theo đường nét đứt như hình sau đó trải tờ giấy ra. Hình vừa cắt được là hình gì?
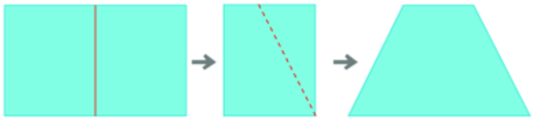
Hình chữ nhật
Hình thang cân
Hình bình hành
Hình thoi.
Cho hình chữ nhật \[ABFE\] và hình thoi \[ABCD\], biết \[CD = 5\,\,{\rm{cm}}\] và \(AE = 2\;\,\,{\rm{cm}}\). Diện tích của hình chữ nhật \[ABFE\] bằng
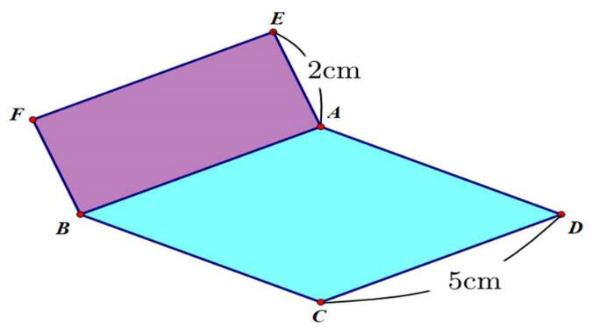
\(14\;\,\,{\rm{c}}{{\rm{m}}^2}\)
\(7\;\,\,{\rm{c}}{{\rm{m}}^2}\)
\(10\;\,\,{\rm{c}}{{\rm{m}}^2}\)
\(5\;\,\,{\rm{c}}{{\rm{m}}^2}\).
Ba đường chéo chính của lục giác \(ABCDEF\) là
\(AB,CD,AC\)
\(AD,FC,EB\)
\(AB,CD,EF\)
\(FE,ED,DC\).
(a) Một năm gồm bốn quý. Viết tập hợp \(A\) các tháng của quý hai trong năm;
(b) Viết tập \(B\) các tháng (dương lịch) có \(30\) ngày.
Một đội thiếu niên khi xếp hàng \[2\,;\,\,3\,;\,\,4\,;\,\,5\] đều thừa một người. Biết số đội viên trong khoảng 100 đến 150 người. Tính số đội viên thiếu niên của đội.
1. Thực hiện phép tính:
(a) \[143\,\,.\,\,126 - 143\,\,.\,\,26\]
(b) \[3\,\,.\,\,{2^6}\,\,.\,\,125\].
2. Tìm \[x\], biết:
(a) \(24 + 3\left( {5 - x} \right) = 27\)
(b) \({\left( {x + 2} \right)^3} - 23 = 41\).
(a) Vẽ hình vuông \[MNPQ\] biết độ dài một cạnh bằng 5 cm.
(b) Cho hình vẽ, biết \[ABCD\] là hình chữ nhật và \[BEFC\] là hình vuông. Biết \[AB\; = 4\] cm và \[BE = 3\] cm. Tính diện tích hình chữ nhật \[AEFD\].
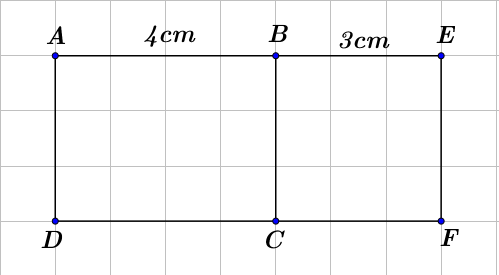
Cho \[A = {2^0}\; + {2^1}\; + {2^2}\; + {2^3}\; + .... + {2^{19}}\]và \[B = {2^{20}}\].
Chứng minh rằng \[A\] và \[B\] là hai số tự nhiên liên tiếp.








