Bộ 10 đề thi giữa kì 1 Toán 6 Cánh diều có đáp án - Đề 3
17 câu hỏi
Cho \(M = \left\{ {a;\,\,5;\,\,b;\,\,c} \right\}\). Khẳng định nào sau đây là sai?
\(5 \in M;\)
\(a \in M;\)
\(d \notin M;\)
\(c \notin M.\)
Cho tập hợp \(M = \left\{ {a;\,\,b;\,\,x;\,\,y} \right\}\). Khẳng định nào sau đây là đúng?
\(a \notin M\)
\(y \in M\)
\(1 \in M\)
\(b \notin M\).
Chữ số hàng trăm trong số \(904\,\,034\) là
0
\(9\,\,040\)
\(904\)
90.
Trong các đồng hồ sau, đồng hồ chỉ \(8\) giờ đúng là đồng hồ nào trong hình?
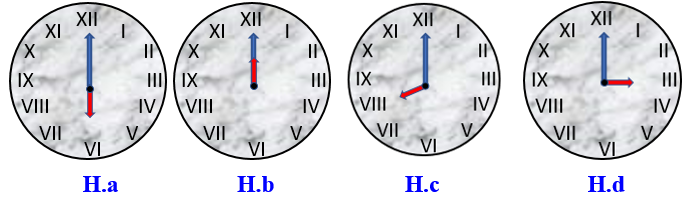
a
b
c
d.
Giá trị của \[x\] trong phép tính \[{2^7}:x = {2^2}\,.\,\,{2^4}\] là
4
3
2
\( - 2\).
Tập hợp các ước của \(17\) là
\(\left\{ {1;\,\,17;\,\,0} \right\}\)
\(\left\{ 1 \right\}\)
\(\left\{ {17} \right\}\)
\(\left\{ {1;\,\,17} \right\}\).
Tổng nào sau đây chia hết cho 6?
\[18 + 36\]
\[55 + 24\]
\[36 + 59\]
\[47 + 12\].
Số tự nhiên \[x\] nhỏ nhất thỏa mãn điều kiện \[x\] chia cho \[12;{\rm{ }}15\]đều dư \[1\] là
\[31\]
\[61\]
\[91\]
\[121\].
Cho tam giác đều \[ABC\] với \[AB = 15\] cm. Độ dài cạnh \[BC\] là
15 cm
7,5 cm
30 cm
5 cm.
Hình chữ nhật \[ABCD\] có cạnh \[AB\] song song với cạnh nào?
\[AD\]
\[CD\]
\[AC\]
\[BD\].
Người ta xếp 6 tam giác đều có chu vi 9 cm thành một hình lục giác đều.
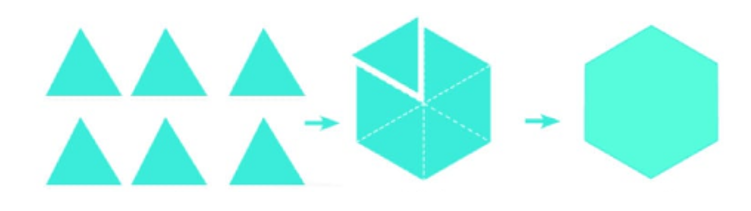
Chu vi của lục giác đều mới là
18 cm
27 cm
36 cm
54 cm.
Chọn đáp án đúng. Quan sát hình vẽ dưới đây và cho biết hình lục giác đều là
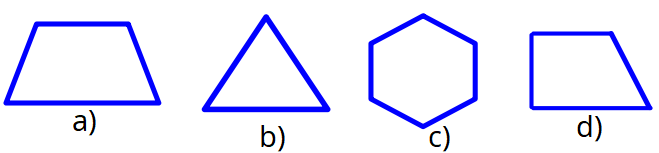
A. Hình (a)
B. Hình (b)
C. Hình (c)
D. Hình (d).
(a) Một năm gồm bốn quý. Viết tập hợp \(A\) các tháng của quý hai trong năm;
(b) Viết tập \(B\) các tháng (dương lịch) có \(30\) ngày.
Một trường đại học cử \(80\) sinh viên nam và \(50\) sinh viên nữ vào Thành phố Hồ Chí Minh để giúp đỡ nhân dân thành phố chống dịch Covid. Trường dự định chia sinh viên thành nhiều nhóm để phục vụ được nhiều nơi, trong đó phân sinh viên nam và nữ đều cho các nhóm. Hỏi có thể chia nhiều nhất bao nhiêu nhóm. Hỏi mỗi nhóm có bao nhiêu nam và nữ?
1. Thực hiện phép tính:
(a) \[122 + 2116 + 278 + 84\]
(b) \(3 \cdot {5^2} + 3:{5^0} - 48:{2^3}\).
2. Tìm \[x\], biết:
(a) \(3x + 43 = 115\)
(b) \({3^x}\,.\,2 + 15 = 33\).
Một mảnh đất hình thoi \[ABCD\] có cạnh bằng 60 m. Ngay bên cạnh, người ta đào một cái ao hình thang cân \[ABEF\] có chiều cao \[FH = 40\] m (như hình vẽ).
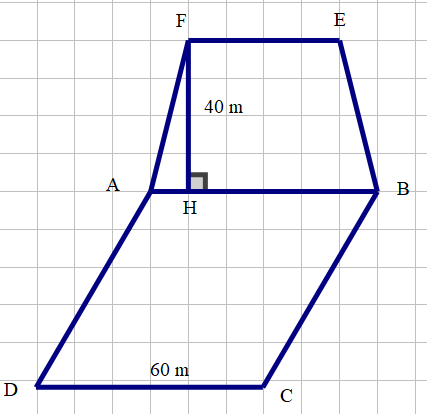
(a) Tính chu vi của mảnh đất \[ABCD\].
(b) Biết đáy \[EF\] nhỏ hơn đáy lớn \[AB\] là 20 m. Tính diện tích của cái ao \[ABEF\].
Cho \(A = 1 + 2 + {2^2} + {2^3} + ... + {2^{2022}}\).
Tính nhanh giá trị biểu thức: \(B = {2^{2023}} - A\).








