12 CÂU HỎI
A. Trắc nghiệm
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn
Trong các hàm số sau, hàm số nào đồng biến trên \(\mathbb{R}?\)
A. \(y = - 3x + 2\).
B. \(y = \frac{{1 - x}}{2}\).
C. \(y = \frac{x}{3} - 1\).
D. \(y = 1 - 2x\).
Cho hàm số \[y = \left( {3m + 2} \right){x^2}\] với \(m = - \frac{2}{3}.\) Giá trị của tham số \[m\] để đồ thì hàm số đã cho đi qua điểm \[\left( { - 1\,;\,\,2} \right)\] là
A. \(m = - \frac{2}{3}.\)
B. \(m = 0.\)
C. \(m = - 1.\)
D. \(m = 1.\)
Cho phương trình \[a{x^2} + bx + c = 0\,\,\,\left( {a \ne 0} \right)\] có biệt thức \(\Delta = {b^2} - 4ac\). Phương trình đã cho vô nghiệm khi
A. \(\Delta < 0\).
B. \(\Delta > 0\).
C. \(\Delta \ge 0\).
D. \(\Delta \le 0\).
Phương trình nào sau đây có hai nghiệm trái dấu?
A. \[{x^2} - 6x + 5 = 0\].
B. \[{x^2} - 5x + 6 = 0\].
C. \[ - {x^2} - 5x - 6 = 0\].
D. \[{x^2} - 5x - 6 = 0\].
Biểu đồ tần số dạng cột là
A. biểu đồ đoạn thẳng với trục ngang biểu diễn tần số.
B. biểu đồ cột với trục ngang biểu diễn tần số.
C. biểu đồ đoạn thẳng với trục đứng biểu diễn tần số.
D. biểu đồ cột với trục đứng biểu diễn tần số.
Cho bảng khảo sát về chiều cao học sinh trong lớp như sau:
|
Chiều cao (cm) |
\(\left[ {150\,;\,\,160} \right)\) |
\(\left[ {160\,;\,\,167} \right)\) |
\(\left[ {167\,;\,\,170} \right)\) |
\(\left[ {170\,;\,\,175} \right)\) |
\(\left[ {175\,;\,\,180} \right)\) |
|
Số học sinh |
\(12\) |
\(18\) |
\(8\) |
\(3\) |
\(1\) |
Bảng số liệu ghép nhóm trên có số nhóm số liệu là
A. \[40\].
B. \[4\].
C. \[5\].
D. \[6\].
Số lượng đôi giày thể thao bán được của một cửa hàng trong bốn năm gần đây được biểu diễn ở biểu đồ sau đây:
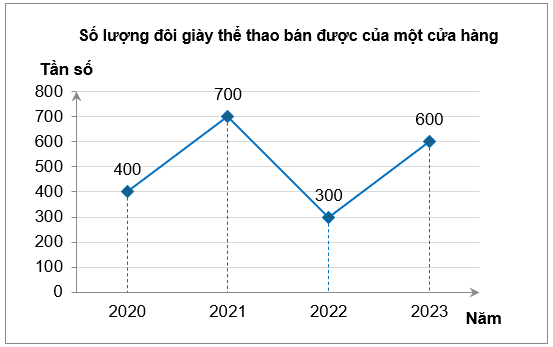
Số đôi giày cửa hàng đã bán được vào năm 2023 là
A. 400.
B. 600.
C. 700.
D. 300.
Khi gieo hai con xúc xắc cân đối và đồng chất, gọi \[T\] là tổng số chấm trên hai con xúc xắc thì kết quả nào sau đây không thể xảy ra?
A. \[T = 1\].
B. \[T = 2.\]
C. \[T = 3.\]
D. \[T = 4.\]
Tâm đường tròn nội tiếp của một tam giác là giao của các đường
A. trung trực.
B. phân giác trong.
C. phân giác ngoài.
D. đường cao.
Cho các hình vẽ sau:
Trong các hình trên, hình nào đang nội tiếp đường tròn?
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Phép quay giữ nguyên mọi điểm là phép quay
A. \(0^\circ \).
B. \(360^\circ \).
C. Cả A và B đều đúng.
D. Cả A và B đều sai.
Cho tam giác \[ABC\] đều nội tiếp đường tròn \[\left( O \right).\] Các phép quay giữ nguyên tam giác \[ABC\] là
A. \[\alpha _1^o = \frac{{360^\circ }}{3} = 120^\circ ;\,\,\alpha _2^o = \frac{{3 \cdot 360^\circ }}{3} = 360^\circ ;\,\,\alpha _3^o = \frac{{2 \cdot 360^\circ }}{3} = 240^\circ .\]
B. \[\alpha _1^o = \frac{{2 \cdot 360^\circ }}{3} = 240^\circ ;\,\,\alpha _2^o = \frac{{360^\circ }}{3} = 120^\circ ;\,\,\alpha _3^o = \frac{{3 \cdot 360^\circ }}{3} = 360^\circ .\]
C. \[\alpha _1^o = \frac{{360^\circ }}{3} = 120^\circ ;\,\,\alpha _2^o = \frac{{2 \cdot 360^\circ }}{3} = 240^\circ ;\,\,\alpha _3^o = \frac{{3 \cdot 360^\circ }}{3} = 360^\circ .\]
D. \[\alpha _1^o = \frac{{3 \cdot 360^\circ }}{3} = 360^\circ ;\,\,\alpha _2^o = \frac{{2 \cdot 360^\circ }}{3} = 240^\circ ;\,\,\alpha _3^o = \frac{{360^\circ }}{3} = 120^\circ .\]
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải