11 CÂU HỎI
A. Trắc nghiệm
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn
Điểm đối xứng với điểm \(\left( {x\,;\,\,y} \right)\) qua trục \(Oy\)là
A. \(\left( {0\,;\,\,0} \right).\)
B. \(\left( { - x\,;\,\,y} \right).\)
C. \(\left( {x\,;\,\,y} \right).\)
D. \[\left( {x\,;\,\, - y} \right).\]
Đồ thị các hàm số \[y = 2x\] và \[y = - \frac{{{x^2}}}{2}\] cắt nhau tại các điểm
A. \(\left( { - \,4\,;\,\, - 8} \right)\).
B. \(\left( {0\,;\,\, - 4} \right)\).
C. \(\left( {0\,;\,\,0} \right)\) và \(\left( { - \,4\,;\,\, - 8} \right)\).
D. \(\left( {0\,;\,\,0} \right)\).
Phương trình nào dưới đây là phương trình bậc hai một ẩn?
A. \({x^4} - 2{x^2} = 0.\)
B. \({x^3} + 3 = 0.\)
C. \(2x - 3 = 0.\)
D. \({x^2} - 2x - 3 = 0.\)
Hai số có tổng bằng 23 và tích của chúng bằng 120 là nghiệm của phương trình nào?
A. \({x^2} - 23x + 120 = 0\).
B. \({x^2} + 23x + 120 = 0\).
C. \({x^2} - 120x + 23 = 0\).
D. \[{x^2} + 120x + 23 = 0\].
Số đo cung tương ứng của hình quạt biểu diễn tần số tương đối \[{f_3} = 20\% \] là
A. \[27^\circ .\]
B. \[74^\circ .\]
C. \[36^\circ .\]
D. \[72^\circ .\]
Bảng phân bố tần số sau đây ghi lại số vé không bán được trong 62 buổi chiếu phim:
|
Lớp |
\[\left[ {0\,;\,\,5} \right)\] |
\[\left[ {5\,;\,\,10} \right)\] |
\[\left[ {10\,;\,\,15} \right)\] |
\[\left[ {15\,;\,\,20} \right)\] |
\[\left[ {20\,;\,\,25} \right)\] |
\[\left[ {25\,;\,\,30} \right)\] |
|
Tần số |
3 |
8 |
15 |
18 |
12 |
6 |
Hỏi có bao nhiêu buổi chiếu phim có nhiều nhất 19 vé không bán được?
A. 42.
B. 43.
C. 44.
D. 45.
Biểu đồ hình quạt tròn bên biểu diễn tỉ lệ người thuộc các nhóm máu ở Việt Nam. Hỏi số người thuộc nhóm máu nào ở Việt Nam chiếm tỉ lệ nhiều nhất?
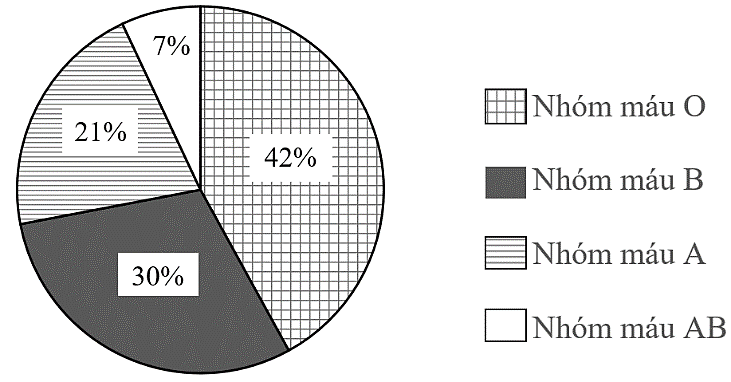
A. Nhóm máu \(O\).B. Nhóm máu \(B\).
C. Nhóm máu \(A\).D. Nhóm máu \(AB.\)
Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được lá bích là
A. \(\frac{1}{{13}}\).
B. \(\frac{1}{4}\).
C. \(\frac{{12}}{{13}}\).
D. \(\frac{3}{4}\).
Đường tròn nội tiếp hình vuông cạnh \[a\] có bán kính là
A. \(a\sqrt 2 \).
B. \(\frac{{a\sqrt 2 }}{2}\).
C. \(\frac{a}{2}\).
D. \(\frac{{a\sqrt 3 }}{2}\).
Khi tứ giác \[MNPQ\] nội tiếp đường tròn, và có \(\widehat M = 90^\circ \). Khi đó, góc \[P\] bằng
A. \(90^\circ \).
B. \(180^\circ \).
C. \(110^\circ \).
D. \(120^\circ \).
Cho ngũ giác đều \[MNPQR\] có tâm \[O.\] Phép quay nào với tâm \[O\] biến ngũ giác đều \[MNPQR\] thành chính nó?
A. \[60^\circ .\]
B. \[72^\circ .\]
C. \[90^\circ .\]
D. \[120^\circ .\]
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
