12 CÂU HỎI
A. Trắc nghiệm
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn
Trong các hàm số sau, hàm số nào đồng biến trên \(\mathbb{R}?\)
A. \(y = - 3x + 2\).
B. \(y = \frac{{1 - x}}{2}\).
C. \(y = \frac{x}{3} - 1\).
D. \(y = 1 - 2x\).
Cho hàm số \[y = a{x^2}\] có đồ thị như hình vẽ bên. Hàm số đó là
A. \[y = 2{x^2}.\]
B. \[y = - 2{x^2}.\]
C. \[y = - {x^2}.\]
D. \[y = {x^2}.\]
Phương trình nào dưới đây là phương trình bậc hai một ẩn?
A. \[\frac{1}{{{x^2}}} + 2026\,x + 2025 = 0\].
B. \({x^4} + 2026\,{x^2} - 2025 = 0\).
C. \({x^2} + 2026\,{x^3} + 2025 = 0\).
D. \({x^2} - 2025\,x + 2026 = 0\).
Gọi \({x_1},\,x{}_2\) là hai nghiệm của phương trình \(2{x^2} + 11x + 7 = 0\), khi đó ta có
A. \({x_1} + {x_2} = \frac{{11}}{2};\,\,{x_1}{x_2} = \frac{7}{2}.\)
B. \({x_1} + {x_2} = - \frac{{11}}{2};\,\,{x_1}{x_2} = \frac{7}{2}.\)
C. \({x_1} + {x_2} = \frac{7}{2};\,\,{x_1}{x_2} = \frac{{11}}{2}.\)
D. \({x_1} + {x_2} = \frac{7}{2};\,\,{x_1}{x_2} = - \frac{{11}}{2}.\)
Trục ngang của biểu đồ tần số tương đối ghép nhóm dạng cột xác định
A. tần số tương đối của nhóm số liệu.
B. đơn vị độ dài phù hợp với các tần số tương đối.
C. các nhóm số liệu cần biểu diễn.
D. tiêu đề cho biểu đồ.
Gieo một con xúc xắc 45 lần cho kết quả như sau:
Số chấm xuất hiện | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
Tần số | \(5\) | \(?\) | \(8\) | \(7\) | \(6\) | \(10\) |
Tần số xuất hiện của mặt \(2\) chấm là
A. 7.
B. 8.
C. 9.
D. 10.
Biểu đồ hình quạt tròn dưới đây biểu diễn tần số tương đối của các ngôn ngữ lập trình được sử dụng khi viết 200 phần mềm của một công ty công nghệ. Biết rằng, mỗi phần mềm được viết bằng đúng một ngôn ngữ lập trình.
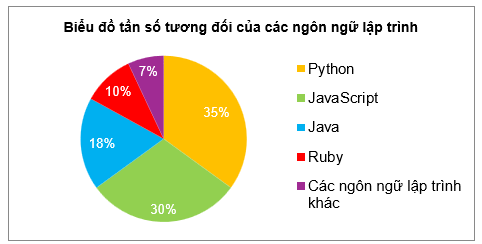
Ngôn ngữ lập trình nào được sử dụng phổ biến nhất trong công ty trên khi viết 200 phần mềm?
A. Python.
B. JavaScript.
C. Java.
D. Ruby.
Một túi đựng 4 viên bi có cùng khối lượng và kích thước, được đánh số 1; 2; 3; 4. Lấy ngẫu nhiên hai viên bi từ trong túi. Số khả năng xảy ra của biến cố A là
A. 3.
B. 4.
C. 5.
D. 6.
Trong các hình dưới đây, đường tròn \[\left( O \right)\] ở hình nào là đường tròn nội tiếp tam giác \[ABC?\]
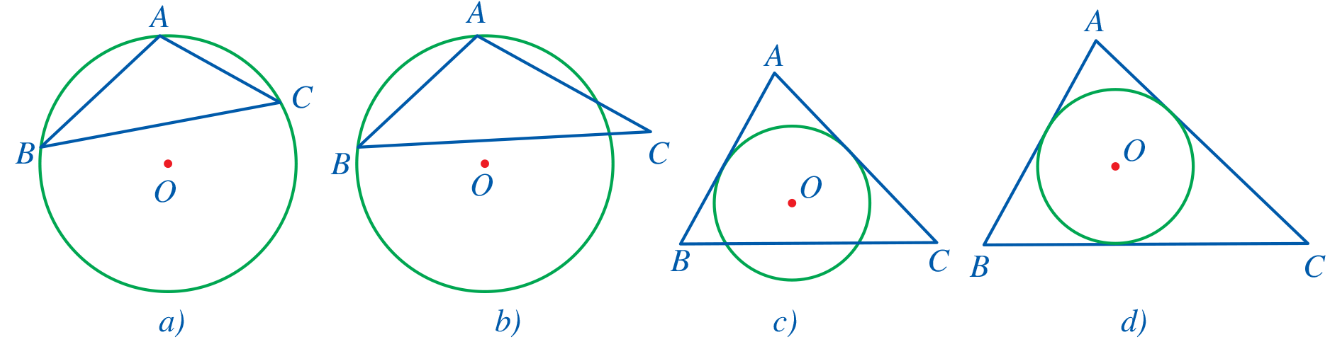
A. Hình a.
B. Hình b.
C. Hình c.
D. Hình d.
Trong các phát biểu sau, phát biểu nào đúng?
A. Mọi tứ giác luôn nội tiếp đường tròn.
B. Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \[90^\circ \].
C. Tổng số đo hai góc đối của một tứ giác nội tiếp luôn bằng \[180^\circ \].
D. Tất cả các hình thang đều là tứ giác nội tiếp.
Cho các hình dưới đây:
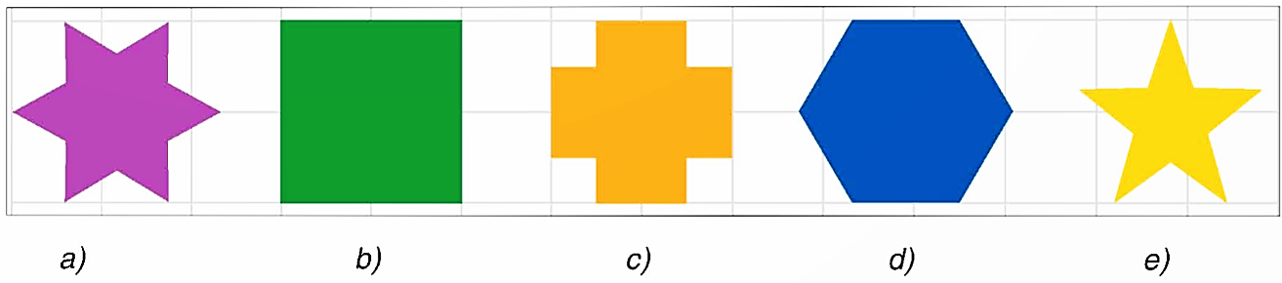
Trong các hình trên, hình nào có dạng là đa giác đều?
A. Hình \(a,\,\,b\).
B. Hình \(b,\,\,d\).
C. Hình \[c,\,\,e\].
D. Hình \(d,\,\,e\).
Cho tam giác \[ABC\] vuông tại \[B\] và góc tại \[A\] bằng \(60^\circ \). Về phía ngoài tam giác vẽ tam giác đều \[ACD\]. Phép quay tâm \[A\] góc \(60^\circ \) biến \[BC\] thành
A. \[AD\].
B. \[DK\] với K là trung điểm của \[AC\].
C. \[CJ\] với \[J\] là trung điểm của \[AD\].
D. \[AI\] với \[I\] là trung điểm của \[CD\].
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải