40 CÂU HỎI
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, BAD = 120°, SA vuông góc với (ABCD). Gọi M, I lần lượt là trung điểm của BC và SB, góc giữa SM và (ABCD) bằng 60°. Khi đó thể tích của khối chóp I.ABCD bằng

A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB=BC=AD=a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ACD.
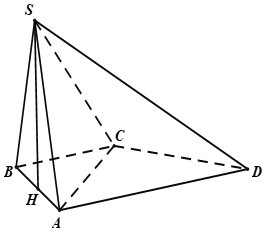
A.
B.
C.
D.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, có BC = a. Mặt bên SAC vuông góc với đáy các mặt bên còn lại đều tạo với mặt đáy một góc 45°. Thể tích khối chóp S.ABC bằng
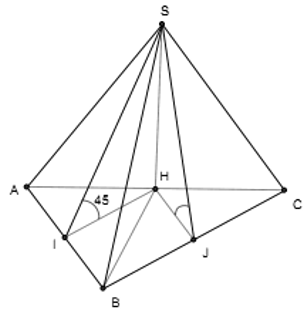
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD), = 30°, SA = 2a. Tính thể tích V của khối chóp S.ABCD.

A.
B.
C.
D.
Cho tứ diện ABCD có ABC là tam giác đều cạnh a tam giác BCD cân tại D và nằm trong mặt phẳng vuông góc với (ABC). Biết AD hợp với mặt phẳng (ABC) một góc 60°. Tính thể tích V của khối tứ diện ABCD.

A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD), = 60°, SA = 2a. Tính thể tích V của khối chóp S.ABCD
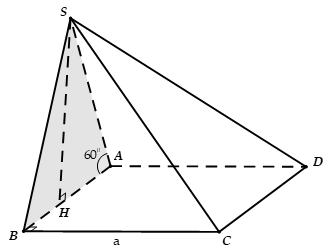
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD, BC = 2AB = 2a tam giác SAC nằm trong mặt phẳng vuông góc với (ABCD), = 60°, SA = 2a. Tính thể tích V của khối chóp S.ABCD
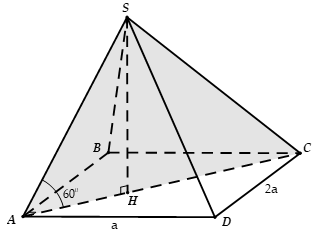
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy là hình vuông tâm O, AB = a. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trung điểm đoạn OA. Góc giữa mặt phẳng (SCD) và mặt phẳng (ABCD) bằng 60°. Tính thể tích V của hình chóp S.ABCD
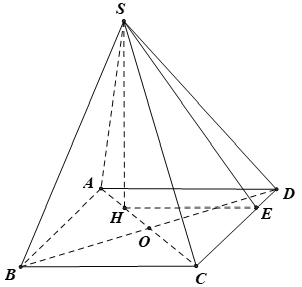
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 1, góc = 60°, cạnh bên SD = . Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là điểm H thuộc đoạn BD sao cho HD = 3HB. Tính thể tích khối chóp S.ABCD.
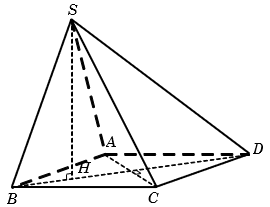
A.
B.
C.
D.
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là trung điểm của BC và SA hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC

A.
B.
C.
D.
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của S trên mặt phẳng (ABC) là trung điểm của BC và (SAB) hợp với đáy một góc 45°. Tính thể tích V của khối chóp S.ABC
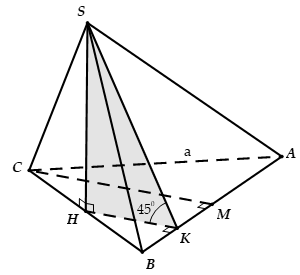
A.
B.
C.
D.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, cạnh AB = 2, = 60°. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của BC. Góc giữa SA và mặt phẳng đáy bằng 45°. Tính thể tích khối chóp S.ABC.
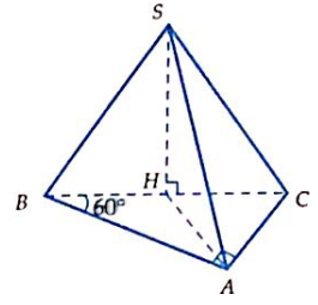
A.
B.
C. 2
D.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, BD = 2a, mặt (SAC) là tam giác vuông tại S và nằm trong mặt phẳng vuông góc với đáy, SC = a. Tính thể tích khối chóp S.ABCD.

A.
B.
C.
D.
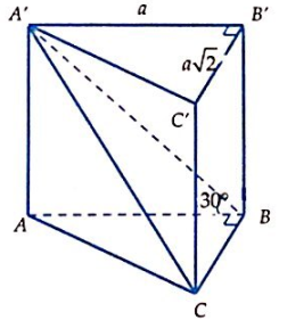
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B; AB = a, BC = a; mặt phẳng (A'BC) hợp với mặt đáy (ABC) góc 30°. Thể tích của khối lăng trụ là:
A.
B.
C.
D.
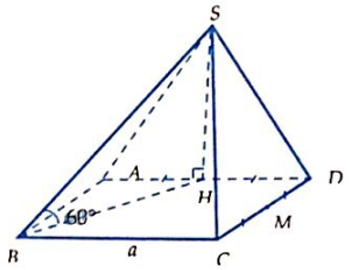
Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trung điểm của AD; M là trung điểm CD; cạnh bên SB hợp với đáy góc 60°. Thể tích của khối chóp S.ABM là:
A.
B.
C.
D.
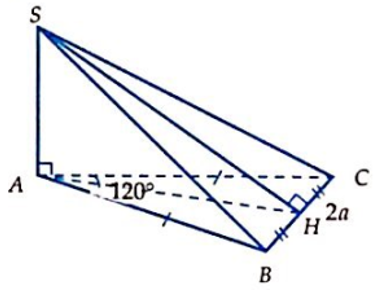
Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A với BC = 2a, = 120°, biết SA ⊥ (ABC) và mặt (SBC) hợp với đáy một góc 45°. Tính thể tích khối chóp S.ABC.
A.
B.
C.
D.
Một lăng trụ tam giác ABC.A'B'C' có đáy là tam giác đều ABC cạnh a. Cạnh bên bằng b và hợp với mặt đáy góc 60°. Thể tích hình chóp A'.BCC'B' bằng bao nhiêu?

A.
B.
C.
D.
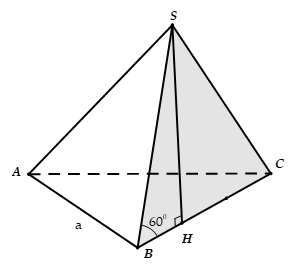
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho , SB hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC
A.
B.
C.
D.
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho , SA hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC

A.
B.
C.
D.
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho , (SAB) hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC

A.
B.
C.
D.
Cho hình chóp S.ABC có các cạnh SA = 1, SB = 2, SC = 3, AB = , BC = CA = . Tính thể tích V khối chóp S.ABC.
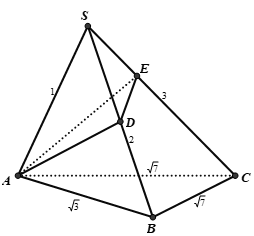
A.
B.
C.
D.
Thể tích khối lăng trụ tam giác đều có cạnh đáy bằng a và cạnh bên bằng 2a là:
A.
B.
C.
D.
Gọi V là thể tích của hình lập phương ABCD.A'B'C'D'. là thể tích của tứ diện A'ABD. Hệ thức nào sau đây là đúng?
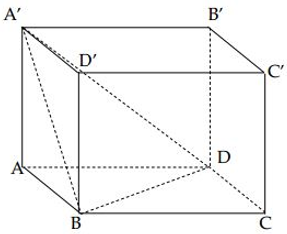
A. V = 6
B. V = 4
C. V = 3
D. V = 2
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại B và AC = 2a biết rằng (A'BC) hợp với đáy (ABC) một góc 45°. Thể tích lăng trụ là:

A.
B.
C.
D.
Cho khối lăng trụ tam giác đều ABC. có tất cả các cạnh bằng a. Gọi M là trung điểm của . Thể tích khối chóp M.BC là:
A.
B.
C.
D.
Cho lăng trụ tam giác đều ABC.A’B’C’, cạnh đáy bằng a. Gọi N, I lần lượt là trung điểm của AB, BC; góc giữa hai mặt phẳng (C’AI) và (ABC) bằng 60°. Tính theo a thể tích khối chóp NAC’I?
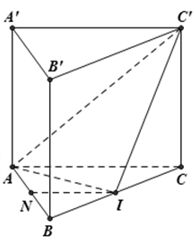
A.
B.
C.
D.
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a và (A’BC) hợp với mặt đáy (ABC) một góc 30°. Tính thể tích hình chóp A’.ABC là
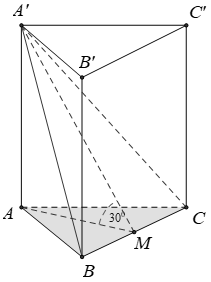
A.
B.
C.
D.
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a. Mặt phẳng (AB’C’) tạo với mặt đáy góc 60°. Tính theo a thể tích lăng trụ ABC.A’B’C’.

A.
B.
C.
D.
Cho lăng trụ đứng ABC. A’B’C’ có đáy ABC là tam giác vuông tại B, AB = 3a, BC = a, mặt bên (A’BC) hợp với mặt đáy (ABC) một góc 60°. Tính thể tích khối lăng trụ.

A.
B.
C.
D.
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AC = a, = 60°. Đường chéo B’C tạo với mặt phẳng (AA’C’C) một góc 30°. Tính thể tích của khối lăng trụ theo a.
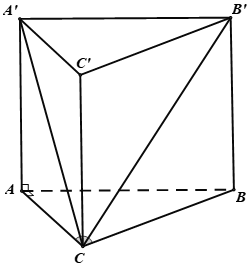
A.
B.
C.
D.
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a; BC = 2a; AA’= a. Lấy điểm M trên cạnh AD sao cho AM = 3MD. Tính thể tích khối chóp M.AB’C.
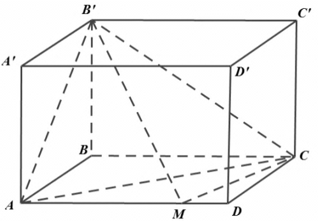
A.
B.
C.
D.
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông cạnh a. Khoảng cách từ điểm A đến mặt phẳng (A’BCD’) bằng . Tính thể tích hình hộp theo a.

A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, = 60° và SA vuông góc với (ABCD). Biết thể tích của khối chóp S.ABCD bằng . Tính khoảng cách (k) từ A đến mặt phẳng (SBC).

A.
B.
C.
C.
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Mặt bên ABB’A’ có diện tích bằng . Gọi M; N lần lượt là trung điểm của A’B; A’C . Tính tỉ số thể tích của hai khối chóp A’. AMN và A’.ABC.
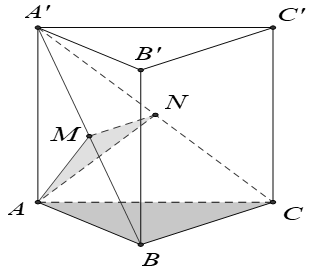
A.
B.
C.
D.
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A’ xuống mặt phẳng (ABC) là trung điểm của AB. Mặt bên (AA’C’C) tạo với đáy một góc bằng 45°. Thể tích khối lăng trụ bằng:
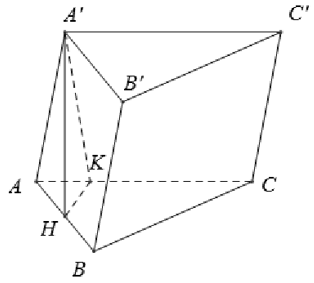
A.
B.
C.
D.
Cho hình lăng trụ ABC.A’B’C’, đáy ABC có AC = a; BC = 3a, = 30°. Cạnh bên hợp với mặt phẳng đáy góc 60° và mặt phẳng (A’BC) vuông góc với mặt phẳng (ABC). Điểm H trên cạnh BC sao cho BC = 3BH và mặt phẳng (A’AH) vuông góc với mặt phẳng (ABC). Thể tích khối lăng trụ ABC.A’B’C’ bằng:
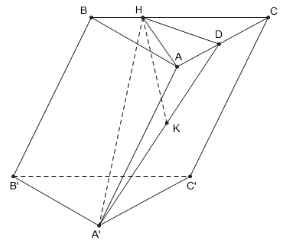
A.
B.
C.
D.
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A’ xuống mặt phẳng (ABC) là trung điểm của AB. Mặt bên (AA’C’C) tạo với đáy một góc bằng 45°. Thể tích của khối lăng trụ ABC.A’B’C’ bằng:
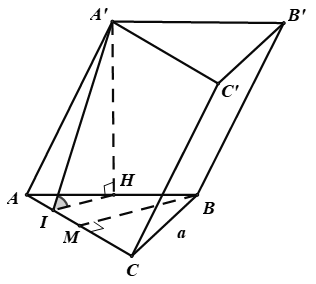
A.
B.
C.
D.
Cho lăng trụ tam giác ABC.A’B’C’ đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc H của A’ trên mặt phẳng (ABC) trùng với trực tâm của tam giác ABC. Tất cả các cạnh bên đều tạo với mặt phẳng đáy góc 60°. Thể tích của khối lăng trụ ABC.A’B’C’là:

A.
B.
C.
D.
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, cạnh bên tạo với mặt phẳng đáy một góc bằng 45°. Hình chiếu của A trên mặt phẳng (A’B’C’) trùng với trung điểm của A’B’. Tính thể tích V của khối lăng trụ theo a.
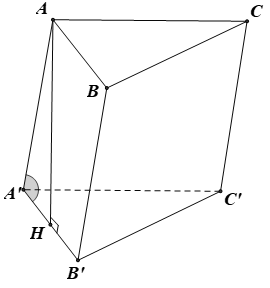
A.
B.
C.
D.
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, = 120° và AA' = 7a/2. Hình chiếu vuông góc của A’ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’.

A. V = 12
B. V = 3
C. V = 9
D. V = 6


