8 CÂU HỎI
Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 3 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích tam giác mới được tạo nên bằng:
A. 2S;
B. 3S;
C. 9S;
D. 6S.
Cho tam giác ABC có AB = 10 cm, AC = 20 cm và có diện tích là 90 cm2. Giá trị sinA là:
A. ;
B. ;
C. ;
D. .
Tam giác ABC có AB = 4, BC = 6, AC = . Điểm M thuộc đoạn BC sao cho MC = 2MB. Tính độ dài cạnh AM.
A. AM = ;
B. AM = 3;
C. AM = ;
D. AM = .
Tam giác ABC có AB = , BC = , CA = . Gọi D là chân đường phân giác trong góc A. Khi đó góc bằng bao nhiêu độ?
A. 45°;
B. 60°;
C. 75°;
D. 90°.
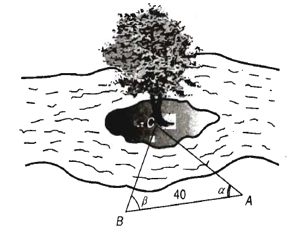
Để đo khoảng cách từ một điểm A bên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C. Ta đo được khoảng cách AB = 40 m, = 45° và = 70°. Vậy sau khi đo đạc và tính toán được, khoảng cách AC gần nhất với giá trị nào sau đây?
A. 53 m;
B. 30 m;
C. 41,5 m;
D. 41 m.
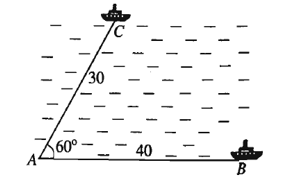
Hai chiếc tàu thuỷ cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo với nhau góc 60°. Tàu B chạy với tốc độ 20 hải lí một giờ. Tàu C chạy với tốc độ 15 hải lí một giờ. Sau hai giờ hai tàu cách nhau bao nhiêu hải lí? (kết quả gần nhất).
A. 61 hải lí;
B. 36 hải lí;
C. 21 hải lí;
D. 18 hải lí.
Tam giác MPQ vuông tại P. Trên cạnh MQ lấy hai điểm E, F sao cho các góc MPE, EPF, FPQ bằng nhau. Đặt MP = q, PQ = m, PE = x, PF = y. Mệnh đề nào sau đây là đúng?
A. ME = EF = FQ;
B. ME2 = q2 + x2 – xq;
C. MF2 = q2 + y2 – yq;
D. MQ2 = q2 + m2 – 2qm.
Tam giác ABC có ba cạnh có độ dài lần lượt là 3, 4, 5. Khi đó, bán kính đường tròn nội tiếp tam giác ABC là
A. ;
B. 4;
C. 2;
D. 1.

