48 CÂU HỎI
Trong không gian cho đường thẳng △ không nằm trong mp (P), đường thẳng ∆ được gọi là vuông góc với mp (P) nếu:
A. vuông góc với hai đường thẳng phân biệt nằm trong mp (P).
B. vuông góc với đường thẳng a mà a song song với mp (P).
C. vuông góc với đường thẳng a nằm trong mp (P).
D. vuông góc với mọi đường thẳng nằm trong mp (P).
Cho đường thẳng d song song với mặt phẳng (α), nếu mặt phẳng (β) chứa d mà cắt (α) theo giao tuyến d’ thì:
A. d ≡ d’
B. d // d’
C. d // (β)
D. d’ // (α).
Cho hình thoi ABCD có AC = BD. Tìm tâm đường tròn ngoại tiếp hình thoi ABCD?
A. Điểm A
B. Giao điểm của AC và BD
C. Không có đường tròn ngoại tiếp tứ giác ABCD
D. Trung điểm cạnh AB.
Tìm một số thập phân biết rằng khi chia số đó cho 3,25 rồi cộng với 24,56 thì được kết quả một số tự nhiên lớn nhất có hai chữ số.
A. 401,57
B. 238,68
C. 2747,25
D. 241,93.
Với các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số gồm 8 chữ số, trong đó chữ số 1 có mặt 3 lần, mỗi chữ số khác có mặt đúng 1 lần.
A. 6 720 số
B. 40 320 số
C. 5 880 số
D. 840 số.
Tính đạo hàm của hàm số \(y = \sqrt {{{\left( {x - 2} \right)}^3}} \).
A. \(\frac{3}{2}\sqrt {x - 2} \)
B. \(\frac{3}{4}\sqrt {x - 2} \left( {x - 2} \right)\)
C. \(\frac{3}{4}\left( {x - 2} \right)\)
D. \(\frac{3}{4}\sqrt {x - 2} {\left( {x - 2} \right)^2}\).
Cho tam giác ABC có trực tâm H. Gọi D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây đúng?
A. \(\overrightarrow {HA} = \overrightarrow {C{\rm{D}}} ;\overrightarrow {A{\rm{D}}} = \overrightarrow {CH} \)
B. \(\overrightarrow {HA} = \overrightarrow {C{\rm{D}}} ;\overrightarrow {A{\rm{D}}} = \overrightarrow {HC} \)
C. \(\overrightarrow {HA} = \overrightarrow {C{\rm{D}}} ;\overrightarrow {AC} = \overrightarrow {CH} \)
D. \(\overrightarrow {HA} = \overrightarrow {C{\rm{D}}} ;\overrightarrow {A{\rm{D}}} = \overrightarrow {HC} ;\overrightarrow {OB} = \overrightarrow {O{\rm{D}}} \).
Cho tam giác ABC vuông cân tại A có \(BC = a\sqrt 2 \). Tính \(\overrightarrow {CA} .\overrightarrow {CB} \).
A. a2
B. a
C. \(\frac{{a\sqrt 2 }}{2}\)
D. \[{\rm{a}}\sqrt 2 \].
Hai xạ thủ cùng bắn vào một tấm bia. Xác suất người thứ nhất bắn trúng là 80%. Xác suất người thứ hai bắn trúng là 70 %. Xác suất hai người cùng bắn trúng là:
A. 50%
B. 32,6%
C. 60%
D. 56%.
Tìm tất cả các giá trị của tham số m sao cho phương trình x3 – 3x2 + (2m – 2)x + m – 3 = 0 có ba nghiệm x1, x2, x3 thỏa mãn x1 < –1 < x2 < x3.
A. m > –5
B. m < –5
C. m ≤ –5
D. m < –6.
Cho 4 điểm bất kì A, B, C, O. Đẳng thức nào sau đây đúng?
A. \(\overrightarrow {OA} = \overrightarrow {OB} - \overrightarrow {BA} \)
B. \(\overrightarrow {OA} = \overrightarrow {CA} - \overrightarrow {CO} \)
C. \(\overrightarrow {AB} = \overrightarrow {AC} + \overrightarrow {BC} \)
D. \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \).
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC vuông tại A, \[{\rm{A}}B = a\sqrt 3 \], AC = AA’ = a. Sin góc giữa đường thẳng AC’ và mặt phẳng (BCC’B’) bằng:
A. \(\frac{{\sqrt {10} }}{4}\)
B. \(\frac{{\sqrt 6 }}{3}\)
C. \(\frac{{\sqrt 3 }}{3}\)
D. \(\frac{{\sqrt 6 }}{4}\).
Viết số thập phân 0,25 dưới dạng phân số ta được:
A. \(\frac{1}{4}\)
B. \(\frac{5}{2}\)
C. \(\frac{2}{5}\)
D. \(\frac{1}{5}\).
Trong mặt phẳng α cho tứ giác ABCD, điểm E ∉ (α). Hỏi có bao nhiêu mặt phẳng phân biệt tạo bởi ba trong năm điểm A, B, C, D, E?
A. 10
B. 7
C. 8
D. 9.
Chọn câu sai. Tứ giác nào có hai đường chéo bằng nhau.
A. Hình vuông
B. Hình thang cân
C. Hình chữ nhật
D. Hình thoi.
Cho 90° < α < 180°. Kết luận nào sau đây đúng
A. sin(α) > 0; cos(α) > 0
B. sin(α) > 0; cos(α) < 0
C. sin(α) < 0; cos(α) > 0
D. sin(α) < 0; cos(α) < 0.
Cho tứ giác lồi ABCD và điểm S không thuộc mp(ABCD). Có bao nhiêu mặt phẳng phân biệt xác định bởi 3 trong số các điểm A, B, C, D, S?
A. 5
B. 6
C. 7
D. 4.
Rút gọn tổng sau: \(S = C_n^1 + 2C_n^2 + 3C_n^3 + ... + nC_n^n\) ta được:
A. S = n . 2n
B. S = 2n+1
C. S = n. 2n-1
D. S = 2n-1.
Cho 2 đường thẳng a, b cắt nhau và không đi qua điểm A. Xác định được nhiều nhất bao nhiêu mặt phẳng bởi a, b và A?
A. 1
B. 2
C. 3
D. 4.
Trong không gian cho 4 điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
A. 6
B. 4
C. 3
D. 2.
Cho hình chóp S.ABCD. Giao tuyến của hai mặt phẳng (SAB) và (SBC) là đường thẳng:
A. SA
B. SD
C. SB
D. AC.
Cho hình trụ có các đáy là 2 hình tròn tâm O và O', bán kính đáy bằng chiều cao vào bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O lấy điểm B sao cho AB = 2a. Thể tích khối tứ diện OO'AB theo a là:
A. \(V = \frac{{\sqrt 3 {a^3}}}{8}\)
B. \(V = \frac{{\sqrt 3 {a^3}}}{4}\)
C. \(V = \frac{{\sqrt 3 {a^3}}}{6}\)
D. \(V = \frac{{\sqrt 3 {a^3}}}{{12}}\).
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD. Giao tuyến của mặt phẳng (ACD) và (GAB) là:
A. AM (M là trung điểm của AB)
B. AN (N là trung điểm của CD)
C. AH (H là hình chiếu của B trên CD)
D. AK (K là hình chiếu của C trên BD).
Cho phép vị tự tâm O tỉ số k ≠ 0 biến điểm M thành điểm M’. Chọn mệnh đề đúng:
A. \(\overrightarrow {OM'} = k\overrightarrow {OM} \)
B. \(\overrightarrow {OM} = k\overrightarrow {OM'} \)
C. \(\overrightarrow {OM'} = - k\overrightarrow {OM} \)
D. \(\overrightarrow {OM'} = \left| k \right|\overrightarrow {OM} \).
Với giá trị nào của m để phương trình 9x – 3x + m = 0 có nghiệm?
A. \(m > \frac{1}{4}\)
B. m < 0
C. m > 0
D. \(m \le \frac{1}{4}\).
Gọi S là tập hợp tất cả các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số y = f(x) = 4x2 – 4mx + m2 – 2m trên đoạn [–2; 0] bằng 3. Tính tổng T các phần tử của S.
A. \(T = - \frac{3}{2}\)
B. \(T = \frac{1}{2}\)
C. \(T = \frac{9}{2}\)
D. \(T = \frac{3}{2}\).
Có bao nhiêu số tự nhiên có 5 chữ số trong đó các chữ số cách đều chữ số đứng giữa thì giống nhau?
A. 900
B. 9 000
C. 90 000
D. 27 216.
Số mặt phẳng đối xứng của hình bát diện đều là:
A. 5
B. 3
C. 7
D. 9.
Một số gấp lên 9 lần rồi bớt đi 13 thì được năm chục. Giá trị của số đó là:
A. 63
B. 5
C. 6
D. 7.
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(–1; –2; 0), B(0; –4; 0), C(0; 0; –3). Phương trình mặt phẳng (P) nào dưới đây đi qua A, gốc tọa độ O và cách đều hai điểm B và C?
A. (P): 6x – 3y + 5z = 0
B. (P): –6x + 3y + 4z = 0
C. (P): 2x – y – 3z = 0
D. (P): 2x – y + 3z = 0.
Giá trị của biểu thức A = tan1° tan2°tan3° ... tan88°tan89° là:
A. 0
B. 2
C. \(\frac{{\sqrt 2 }}{2}\)
D. 1.
Trong mp(α), cho bốn điểm A, B, C, D trong đó không có ba điểm nào thẳng hàng. Điểm S ∉ mp(α). Có mấy mặt phẳng tạo bởi S và hai trong số bốn điểm nói trên?
A. 4
B. 5
C. 6
D. 8.
Tâm đối xứng của đồ thị hàm số \(y = \frac{{ax + b}}{{c{\rm{x}} + d}}\) là:
A. I(0; 0)
B. \(I\left( {\frac{{ - d}}{c};\frac{a}{c}} \right)\)
C. \(I\left( {\frac{a}{c};\frac{{ - d}}{c}} \right)\)
D. \(I\left( {\frac{d}{c};\frac{b}{a}} \right)\).
Với a là số thực dương bất kì, mệnh đề nào dưới đây đúng?
A. log(3a) = 3log a
B. \(\log {a^3} = \frac{1}{3}\log a\)
C. log a3 = 3log a
D. \(\log \left( {3a} \right) = \frac{1}{3}\log a\).
Cho hình nón có đường cao h = 5a và bán kính đáy r = 12a. Gọi (α) là mặt phẳng đi qua đỉnh của hình nón và cắt đường tròn theo dây cũng có độ dài 10a. Tính diện tích thiết diện tạo bởi mặt phẳng (α) và hình nón đã cho.
A. 69a2
B. 120a2
C. 60a2
D. \(\frac{{119{{\rm{a}}^2}}}{2}\).
Đường tròn ngoại tiếp hình vuông cạnh bằng 2 có bán kính là:
A. 1
B. 2
C. \(\sqrt 2 \)
D. \(2\sqrt 2 \).
Nghiệm của phương trình sin2x + cosx = 0 là:
A. \(\left[ \begin{array}{l}x = - \frac{\pi }{2} + k\pi \\x = - \frac{\pi }{6} + \frac{{k2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
B. \(\left[ \begin{array}{l}x = - \frac{\pi }{2} + k2\pi \\x = \frac{\pi }{2} + \frac{{k2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
C. \(\left[ \begin{array}{l}x = \frac{\pi }{2} + k2\pi \\x = \frac{\pi }{6} + \frac{{k\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
D. \(\left[ \begin{array}{l}x = - \frac{\pi }{2} + k\pi \\x = \frac{\pi }{4} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
Tìm tất cả các giá trị của tham số m để phương trình 9x – (m – 1) . 3x + 2m = 0 có nghiệm duy nhất.
A. \(m = 5 + 2\sqrt 6 \)
B. \(m = 0;m = 5 + 2\sqrt 6 \)
C. \(m < 0;m = 5 \pm 2\sqrt 6 \)
D. \(m < 0;m = 5 + 2\sqrt 6 \).
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên:
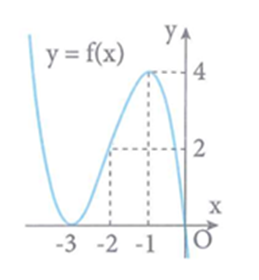
Số nghiệm thực của phương trình 2f (x2 – 1) – 5 = 0.
A. 1
B. 3
C. 4
D. 2.
Tính \(\sqrt {49} \).
A. –7
B. 49
C. \( \pm 7\)
D. 7.
“ Nếu ta chia cả tử và mẫu của một phân số cho cùng một … của chúng thì ta được một phân số mới … phân số đã cho”. Các cụm từ thích hợp vào chỗ trống lần lượt là:
A. ước chung, bằng
B. bội chung, lớn nhất
C. số, bằng
D. tích, bằng.
Cho hình vuông tâm O. Hỏi có bao nhiêu phép quay tâm O góc α, 0 ≤ α < 2π biến hình vuông trên thành chính nó?
A. 6
B. 2
C. 3
D. 4.
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a, CD = a. Gọi I là trung điểm cạnh AD, biết hai mặt phẳng (SBI), (SCI) cùng vuông góc với đáy và thể tích khối chóp S.ABCD bằng \(\frac{{3\sqrt {15} {a^3}}}{5}\). Tính góc giữa hai mặt phẳng (SBC) và (ABCD).
A. 30°
B. 36°
C. 45°
D. 60°.
Không gian mẫu khi gieo hai đồng xu là:
A. Ω ={SS; NN; NS; SN}
B. Ω ={SS; NN; SN}
C. Ω ={SS; NN}
D. Ω ={SS; SN}.
Tập nghiệm của bất phương trình \(\frac{{{3^x}}}{{{3^x} - 2}} < 3\) là:
A. \(\left[ \begin{array}{l}x > 1\\x < {\log _3}2\end{array} \right.\)
B. x > log32
C. x < 1
D. log32 < x < 1.
Khi sản xuất vỏ lon sữa bò hình trụ có thể tích là V, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ lon sữa bò là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể tích khối trụ bằng V và diện tích toàn phần hình trụ nhỏ nhất thì bán kính đáy bằng bao nhiêu?
A. \(r = \sqrt[3]{{\frac{{V\pi }}{2}}}\)
B. \(r = \sqrt[3]{V}\)
C. \(r = \sqrt[3]{{\frac{V}{{2\pi }}}}\)
D. \(r = \sqrt[3]{{\frac{V}{2}}}\).
Kí hiệu nào sau đây dùng để viết đúng mệnh đề “\(\sqrt 2 \) không phải là số hữu tỉ”?
A. \(\sqrt 2 \ne \mathbb{Q}\)
B. \(\sqrt 2 \not\subset \mathbb{Q}\)
C. \(\sqrt 2 \notin \mathbb{Q}\)
D. \(\sqrt 2 \in \mathbb{Q}\).
Cho tập hợp A={1; 2; 3; 4; a; b}. Xét các mệnh đề sau đây:
(I): “3 ∈ A”.
(II): “{3; 4} ∈ A”.
(III): “{a; 3; b} ∈ A”.
Trong các mệnh đề sau, mệnh đề nào đúng?
A. I đúng
B. I, II đúng
C. II đúng
D. III đúng.

