14 CÂU HỎI
Cho bất phương trình 2x + 3y − 6 ≤ 0 (1). Chọn khẳng định đúng trong các khẳng định sau:
A. Bất phương trình (1) chỉ có một nghiệm duy nhất;
B.Bất phương trình (1) vô nghiệm;
C. Bất phương trình (1) luôn có vô số nghiệm;
D. Bất phương trình (1) có tập nghiệm là ℝ.
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 3y - 6 < 0\\x \ge 0\\2x - 3y - 1 \le 0\end{array} \right.\) chứa điểm nào sau đây?
A. A(1; 2);
B.B(0; 2);
C. C(−1; 3);
D. \(D\left( {0;\; - \frac{1}{3}} \right)\).
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?
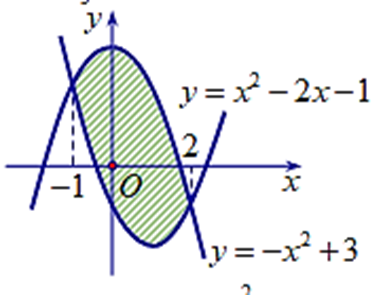
A. \(\int\limits_{ - 1}^2 {\left( {2{x^2} - 2x - 4} \right)dx} \);
B.\(\int\limits_{ - 1}^2 {\left( { - 2x + 2} \right)dx} \);
C. \(\int\limits_{ - 1}^2 {\left( {2x - 2} \right)dx} \);
D. \(\int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx} \).
Cho các mệnh đề sau:
a. Nếu a // (P) thì a song song với mọi đường thẳng nằm trong (P).
b. Nếu a // (P) thì a song song với một đường thẳng nào đó nằm trong (P).
c. Nếu a // (P) thì có vô số đường thẳng nằm trong (P) và song song với a
d. Nếu a // (P) thì có một đường thẳng d nào đó nằm trong (P) sao cho a và d đồng phẳng.
Số mệnh đề đúng là:
A. 1;
B. 2;
C.3;
D. 4.
Trong các mệnh đề sau, mệnh đề nào sai?
A. Nếu đường thẳng a song song với mặt phẳng (P) và đường thẳng b vuông góc với a thì b vuông góc với mặt phẳng (P);
B. Nếu đường thẳng a song song với đường thẳng b và b song song với mặt phẳng (P) thì a song song hoặc nằm trên mặt phẳng (P);
C. Nếu đường thẳng a song song với mặt phẳng (P) và đường thẳng b vuông góc với mặt phẳng (P) thì a vuông góc với b;
D. Một đường thẳng vuông góc với hai đường thẳng cắt nhau trong một mặt phẳng thì nó vuông góc với mặt phẳng đó.
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD, M là trung điểm CD, I là điểm ở trên đoạn thẳng AG, BI cắt mặt phẳng (ACD) tại J. Khẳng định nào sau đây sai?
A. AM = (ACD) Ç (ABG);
B.A, J, M thẳng hàng;
C. J là trung điểm của AM;
D. DJ = (ACD) Ç (BDJ).
Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a. Mệnh đề nào sau đây là sai?
A.\(\overrightarrow {AB} \,.\,\overrightarrow {AC} = \frac{1}{2}{a^2}\);
B.\(\overrightarrow {AC} \,.\,\overrightarrow {CB} = - \frac{1}{2}{a^2}\);
C. \(\overrightarrow {GA} \,.\,\overrightarrow {GB} = \frac{{{a^2}}}{6}\);
D. \(\overrightarrow {AB} \,.\,\overrightarrow {AG} = \frac{1}{2}{a^2}\).
Trong mặt phẳng Oxy cho đường thẳng d: 2x − y + 1 = 0. Để phép quay tâm I góc quay 2017p biến d thành chính nó thì tọa độ của I là:
A. (2; 1);
B. (2; −1);
C. (1; 0);
D. (0; 1).
Phát biểu nào sau đây là đúng?
A. Nếu f ¢(x) đổi dấu từ dương sang âm khi x qua điểm x0 và f (x) liên tục tại x0 thì hàm số y = f (x) đạt cực đại tại điểm x0;
B. Hàm số y = f (x) đạt cực trị tại x0 khi và chỉ khi x0 là nghiệm của f ¢(x) = 0;
C. Nếu f ¢(x0) = 0 và f ¢¢(x0) = 0 thì x0 không là điểm cực trị của hàm số y = f (x);
D. Nếu f ¢(x0) = 0 và f ¢¢(x0) > 0 thì hàm số đạt cực đại tại x0.
Phần không tô đậm trong hình vẽ dưới đây (không chứa biên), biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?
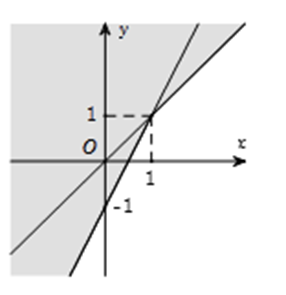
A. \[\left\{ \begin{array}{l}x - y \ge 0\\2x - y \ge 1\end{array} \right.\];
B. \[\left\{ \begin{array}{l}x - y > 0\\2x - y > 1\end{array} \right.\];
C. \[\left\{ \begin{array}{l}x - y < 0\\2x - y > 1\end{array} \right.\];
D. \[\left\{ \begin{array}{l}x - y < 0\\2x - y < 1\end{array} \right.\].
Phần không tô đậm trong hình vẽ dưới đây (không chứa biên), biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?
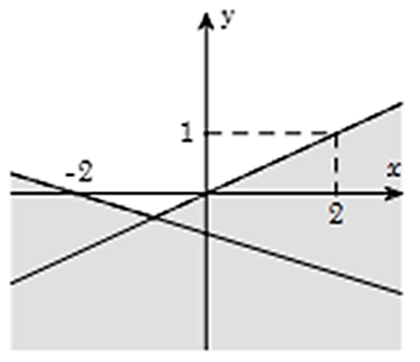
A. \[\left\{ \begin{array}{l}x - 2y \le 0\\x + 3y \ge - 2\end{array} \right.\];
B. \[\left\{ \begin{array}{l}x - 2y > 0\\x + 3y < - 2\end{array} \right.\];
C. \[\left\{ \begin{array}{l}x - 2y \le 0\\x + 3y \le - 2\end{array} \right.\];
D. \[\left\{ \begin{array}{l}x - 2y < 0\\x + 3y > - 2\end{array} \right.\].
Trong mặt phẳng Oxy, phép quay tâm O góc quay 90° biến đường thẳng d: x − y + 1 = 0 thành đường thẳng có phương trình là:
A. x + y − 3 = 0;
B. x − y + 1 = 0;
C. x − y + 3 = 0;
D. x + y + 1 = 0.
Nếu tam giác ABC có a2 < b2 + c2 thì:
A. góc A nhọn;
B. góc A tù;
C. góc A vuông;
D. góc A là góc nhỏ nhất.
Cho tam giác ABC có a2 + b2 − c2 > 0. Khi đó:
A. \[\widehat C > 90^\circ \];
B.\[\widehat C < 90^\circ \];
C. \[\widehat C = 90^\circ \];
D. Không thể kết luận được gì về góc C.
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
