22 CÂU HỎI
Cho 6 điểm A, B, C, D, E, F. Đẳng thức nào sau đây đúng?
A.
B.
C.
D.
Cho tam giác OAB vuông cân tại O, cạnh OA = a. Khẳng định nào sau đây sai?
A.
B.
C.
D.
Lớp 10A có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hoá, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả ba môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10A là
A. 9.
B. 18.
C. 10.
D. 28.
Cho hàm số y = f(x) xác định, liên tục trên ℝ và có bảng biến thiên sau:
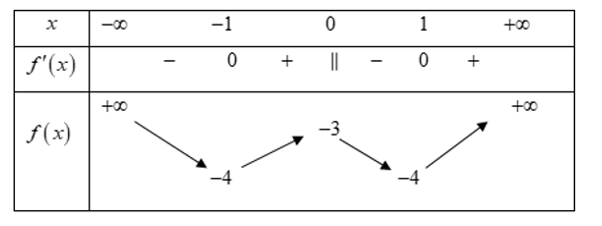
Khẳng định nào sau đây là đúng?
A. Hàm số có ba giá trị cực trị.
B. Hàm số có ba điểm cực trị.
C. Hàm số có hai điểm cực trị.
D. Hàm số đạt cực đại tại điểm x = 1.
Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng cổ. Mỗi vòng tay làm trong 4 giờ, bán được 40 ngàn đồng. Mỗi vòng cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn An bán được không quá 15 vòng tay và 4 vòng cổ. Tính số giờ tối thiểu trong tuần An cần dùng để bán được ít nhất 400 ngàn đồng?
D. Hàm số đạt cực đại tại điểm x = 1.
Có bao nhiêu loại khối đa diện đều?
A. 3.
B. 5.
C. 6.
D. 7.
Có bao nhiêu phép tịnh tiến biến một đường tròn cho trước thành chính nó?
A. 0.
B. 1.
C. 2.
D. Vô số.
Mệnh đề: "Tổng các lập phương của hai số a và b" được biểu thị bởi:
A.
B.
C.
D.
Cho bốn điểm không đồng phẳng, ta có thể xác định được nhiều nhất bao nhiêu mặt phẳng phân biệt từ bốn điểm đã cho?
A. 2.
B. 3.
C. 4.
D. 6.
Cho hàm số có đồ thị như dưới đây.
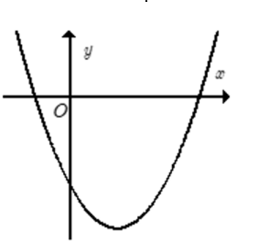
Khẳng dịnh nào sau đây đúng?
A. a > 0, b < 0, c < 0.
B. a > 0, b < 0, c > 0.
C. a > 0, b > 0, c > 0.
D. a < 0, b < 0, c > 0.
Cho hàm số f(x) có bảng biến thiên như sau:
![Cho hàm số f(x) có bảng biến thiên như sau: Số nghiệm thuộc đoạn [π; 2π] của phương trình 2f(sin x) + 3 = 0 là: A. 4. B. 6. C. 3. D. 8. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/09/blobid5-1694745831.png)
Số nghiệm thuộc đoạn [-π; 2π] của phương trình 2f(sin x) + 3 = 0 là:
A. 4.
B. 6.
C. 3.
D. 8.
Cho tam giác ABC với H, O, G lần lượt là trực tâm, tâm đường tròn ngoại tiếp, trọng tâm của tam giác. Hệ thức đúng là:
A.
B.
C.
D.
Cho hai góc nhọn α và β (α < β). Khẳng định nào sau đây là sai?
A. cos α < cos β.
B. sin α < sin β.
C. tan α + tan β > 0.
D. cot α > cot β.
Parabol đạt giá trị nhỏ nhất bằng 4 tại x = -2 và đi qua A(0; 6) có phương trình là
A.
B.
C.
D.
Miền biểu diễn nghiệm của hệ bất phương trình có diện tích bằng bao nhiêu?
A. 18.
B. 25.
C. 4.
D. 9.
Thiết diện qua trục của hình trụ là một hình chữ nhật có diện tích bằng 10. Diện tích xung quanh của hình trụ đó bằng:
A. 10π.
B. 10.
C. 5π.
D. 5.
Thiết diện qua trục của một hình trụ là một hình vuông có cạnh bằng 2a. Tính theo a thể tích khối trụ đó.
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc với (ABCD). Hình chóp này có mặt đối xứng nào?
A. Không có.
B. (SAB).
C. (SAC).
D. (SAD).
Tìm mệnh đề đúng trong các mệnh đề sau:
A. Nếu hình H có mặt đối xứng và có tâm đối xứng nằm trên mặt đối xứng thì nó có ít nhất một tâm đối xứng.
B. Nếu hình H có trục đối xứng thì nó có ít nhất một tâm đối xứng.
C. Nếu hình H có mặt đối xứng thì nó có ít nhất một trục đối xứng.
D. Nếu hình H có mặt đối xứng và có trục đối xứng thì nó có ít nhất một tâm đối xứng.
Hàm só nào sau đây nghịch biến trên từng khoảng xác định?
A. y = 2x – sin x.
B. y = -x3 + 3x2.
C.
D. y = x4 – x2.
Hình dưới đây có tất cả bao nhiêu hình vuông?
A. 10.
B. 9.
C. 14.
D. 13.
Trong mặt phẳng Oxy cho điểm M(1; 1). Hỏi trong bốn điểm được cho ở các phương án dưới đây, điểm nào là ảnh của M qua phép quay tâm O, góc
A. A(1; 0).
B.
C.
D. D(-1; 1).
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
