17 CÂU HỎI
Đa thức P (x) = 32x5 − 80x4 + 80x3 − 40x2 + 10x − 1 là khai triển của nhị thức nào dưới đây?
A. (1 − 2x)5;
B. (1 + 2x)5;
C. (2x − 1)5;
D. (x − 1)5.
Cho đoạn thẳng AB. Vị trí của điểm M thỏa mãn: được xác định bởi:
A.
B.
C.
D.
Cho hai điểm A, B phân biệt. Xác định điểm M biết .
A. M nằm trên tia AB và AM = 4AB;
B. M nằm trên tia AB và AM = AB;
C. M nằm trên tia AB và AM = 3AB;
D. M nằm trên tia AB và AM = 2AB.
Cho hình tứ diện ABCD. Gọi I, J lần lượt thuộc cạnh AD, BC sao cho IA = 2ID, JB = 2JC. Gọi (P) là mặt phẳng qua IJ và song song với AB. Khẳng định nào đúng?
A. CD cắt (P);
B. (P) // CD;
C. IJ // CD;
D. IJ // AB.
Cho hàm số . Hệ thức nào sau đây là hệ thức đúng?
A. xy¢ + 7 = −ey;
B. xy¢ − 1 = ey;
C. xy¢ + 1 = ey;
D. xy¢ − 7 = ey.
Cho hàm số . Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên (−∞; 1) È (1; +∞);
B. Hàm số nghịch biến trên (−∞; 1) và (1; +∞);
C. Hàm số nghịch biến trên (−∞; 1) È (1; +∞);
D. Hàm số nghịch biến trên ℝ \ {1}.
Cho hàm số y = f (x) thỏa mãn f ¢(x) = x2 − 5x + 4. Khẳng định nào sau đây là đúng?
A. Hàm số đã cho đồng biến trên khoảng (−∞; 3);
B. Hàm số đã cho nghịch biến trên khoảng (3; +∞);
C. Hàm số đã cho nghịch biến trên khoảng (2; 3);
D. Hàm số đã cho đồng biến trên khoảng (1; 4).
Cho các số phức z thỏa mãn |z − 2i| = |z + 2|. Gọi z là số phức thỏa mãn |(2 − i)z + 5| nhỏ nhất. Khi đó:
A. 0 < |z| < 1;
B. 1 < |z| < 2;
C. 2 < |z| < 3;
D. |z| > 3.
Trong mặt phẳng với hệ tọa độ Oxy, cho các điểm A(4; 0), B(1; 4) và C(1; −1). Gọi G là trọng tâm tam giác ABC. Biết rằng G là điểm biểu diễn số phức z. Mệnh dề nào sau đây là đúng?
A.
B.
C. z = 2 − i;
D. z = 2 + i.
Hình nào sau đây không có tâm đối xứng?
A. Hình vuông;
B. Hình tròn;
C. Hình tam giác đều;
D. Hình thoi.
Hình nào sau đây không có tâm đối xứng?
A. Hình thoi;
B. Hình hình bình hành;
C. Hình thang cân;
D. Hình chữ nhật.
Biến đổi thành , với . Khi đó f (t) là hàm số nào trong các hàm số sau đây?
A. f (t) = 2t2 − 2t;
B. f (t) = t2 + t;
C. f (t) = t2 − t;
D. f (t) = 2t2 + 2t.
Trong mặt phẳng tọa độ Oxy cho 4 điểm A(2; 5); B(1; 7); C(1; 5); D(0; 9). Ba điểm nào sau đây thẳng hàng.
A. Ba điểm A, B, D;
B. Ba điểm A, B, C;
C. Ba điểm B, C, D;
D. Ba điểm A, C, D.
Cho 4 điểm A(1; −2); B(0; 3); C(−3; 4); D(−1; 8). Ba điểm nào trong 4 điểm đã cho là thẳng hàng?
A. A, B, C;
B. B, C, D;
C. A, B, D;
D. A, C, D.
Cho hàm số y = f (x) có đạo hàm trên (a; b). Phát biểu nào sau đây là đúng?
A. Hàm số y = f (x) đồng biến trên (a ; b) khi và chỉ khi f ′(x) ≥ 0"xÎ(a; b) và f ′(x) = 0 tại hữu hạn giá trị x Î(a; b);
B. Hàm số y = f (x) đồng biến trên (a ; b) khi và chỉ khi f ′(x) < 0"xÎ(a; b);
C. Hàm số y = f (x) đồng biến trên (a ; b) khi và chỉ khi f ′(x) £ 0"xÎ(a; b);
D. Hàm số y = f (x) đồng biến trên (a ; b) khi và chỉ khi f ′(x) ≥ 0"xÎ(a; b);
Cho hàm số y = f (x) có đạo hàm trên khoảng (a; b). Mệnh đề nào sau đây sai?
A. Nếu f ′(x) < 0 với mọi x Î (a; b) thì hàm số y = f (x) nghịch biến trên (a; b);
B. Nếu f ′(x) > 0 với mọi x Î (a; b) thì hàm số y = f (x) đồng biến trên (a; b);
C. Nếu hàm số y = f (x) nghịch biến trên (a; b) thì f ′(x) £ 0 với mọi x Î (a; b);
D. Nếu hàm số y = f (x) đồng biến trên (a; b) thì f ′(x) > 0 với mọi x Î (a; b).
Cho hàm số y = f (x) liên tục trên ℝ và có đồ thị như hình
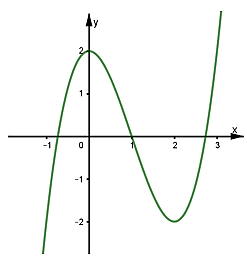
Gọi m là số nghiệm của phương trình f(f(x))= 1. Khẳng định nào sau đây là đúng?
A. m = 6;
B. m = 7;
C. m = 5;
D. m = 9.
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
