40 CÂU HỎI
Cho lăng trụ đứng ABC.A’B’C’, đáy ABC là tam giác vuông tại A. E là trung điểm của B’C’, CB’ cắt BE tại M. Tính thể tích V của khối tứ diện ABCM biết AB = 3a, AA’ = 6a.
A. V = 6a3;
B. \[V = 6\sqrt 2 {a^3}\];
C. V = 8a3;
D. V = 7a3.
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, biết BA = BC = 2a và (A’BC) hợp với đáy một góc 30°. Tính thể tích khối lăng trụ ABC.A’B’C’ là:
A. 6a3;
B. \(\frac{{4{a^3}\sqrt 3 }}{9}\);
C. \(4{a^3}\sqrt 3 \);
D. \(\frac{{4{a^3}\sqrt 3 }}{3}\).
Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, tâm O và \(\widehat {ABC} = 120^\circ \). Các cạnh AA', A'B, A'D cùng tạo với đáy một góc 60°. Tính theo a thể tích V của khối lăng trụ đã cho.
A. \({a^3}\sqrt 3 \);
B. \(\frac{{{a^3}\sqrt 3 }}{6}\);
C. \(\frac{{{a^3}\sqrt 3 }}{2}\);
D. \(\frac{{3{a^2}}}{2}\).
Trong các mệnh đề sau, mệnh đề nào sai?
A. Khối tứ diện là khối đa diện lồi;
B. Lắp ghép 2 khối hộp sẽ được 1 khối đa diện lồi;
C. Khối lập phương là khối đa diện lồi;
D. Khối lăng trụ tam giác là khối đa diện lồi.
Trong các mệnh đề sau, mệnh đề nào sai?
A. Tồn tại tứ diện là khối tứ diện đều;
B. Tồn tại khối lăng trụ đều là khối đa diện đều;
C. Tồn tại khối hộp là khối đa diện đều;
D. Tồn tại khối chóp tứ giác đều là khối da diện đều.
Tìm một số tự nhiên có hai chữ số,biết rằng nếu viết thêm chữ số 6 vào bên trái số đó ta được một số lớn gấp 13 lần số đã cho.
A. 31;
B. 87;
C. 50;
D. 51.
Cho phương trình (m + 1).16x − 2( 2m − 3) .4x + 6m + 5 = 0 với m là tham số thực. Tập tất cả các giá trị của m để phương trình có hai nghiệm trái dấu có dạng (a; b). Tính P = a.b.
A. 4;
B. −4;
C. 5;
D. −5.
Tìm tất cả các giá trị thực của tham số m để phương trình mx – m = 0 vô nghiệm.
A. m ∈∅;
B. m = 0;
C. m ∈ ℝ;
D. m ∈ ℤ.
Cho một khối chóp có thể tích bằng V. Khi giảm chiều cao của hình chóp xuống 2 lần và tăng diện tích đáy lên 4 lần thì thể tích khối chóp lúc đó bằng:
A. \(\frac{{2V}}{3}\);
B. 2V;
C. 3V;
D. \(\frac{V}{2}\).
Phương trình \(2{\sin ^2}x + \sqrt 3 \sin 2x = 3\) có nghiệm là
A. \(x = \frac{\pi }{3} + k\pi \), k ∈ ℤ;
B. \(x = \frac{{2\pi }}{3} + k\pi \), k ∈ ℤ;
C. \(x = \frac{{4\pi }}{3} + k\pi \), k ∈ ℤ;
D. \(x = \frac{{5\pi }}{3} + k\pi \), k ∈ ℤ.
Thể tích khối lăng trụ tam giác đều có cạnh đáy bằng a và cạnh bên bằng 2a bằng:
A. \(\frac{{{a^3}\sqrt 2 }}{3}\);
B. \(\frac{{{a^3}\sqrt 3 }}{6}\);
C. \(\frac{{{a^3}\sqrt 3 }}{2}\);
D. \(\frac{{{a^3}\sqrt 3 }}{4}\).
Thể tích của khối lăng trụ đứng tam giác đều có cạnh bên bằng a, cạnh đáy bằng 2a bằng:
A. \(2{a^3}\sqrt 3 \);
B. \(\frac{{{a^3}\sqrt 3 }}{2}\);
C. \({a^3}\sqrt 3 \);
D. 2a3.
Cho hàm số y = log2x2. Khẳng định nào sau đây là sai?
A. Hàm số đồng biến trên (0; +∞);
B. Hàm số nghịch biến trên (−∞; 0);
C. Đồ thị hàm số có một tiệm cận ngang;
D. Đồ thị hàm số có một đường tiệm cận đứng.
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình 2f(x2 – 1) – 5 = 0 là:
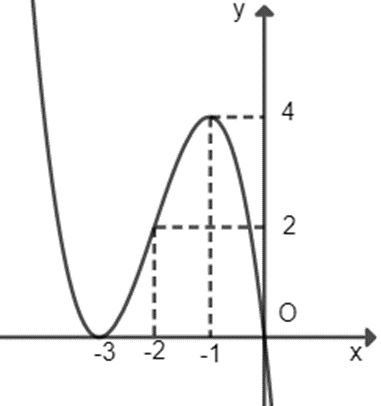
A. 3;
B. 2;
C. 6;
D. 4.
Giá trị của tan30° + cot30° bằng bao nhiêu?
A. \(\frac{4}{{\sqrt 3 }}\);
B. \(\frac{{1 + \sqrt 3 }}{3}\);
C. \(\frac{2}{{\sqrt 3 }}\);
D. 2.
Tập nghiệm của phương trình \({5^x}{.8^{\frac{{x - 1}}{x}}} = 500\) là
A. \(\left[ \begin{array}{l}x = 3\\x = - {\log _5}2\end{array} \right.\);
B. \(\left[ \begin{array}{l}x = 3\\x = {\log _5}2\end{array} \right.\);
C. \(\left[ \begin{array}{l}x = 1\\x = - {\log _5}2\end{array} \right.\);
D. \(\left[ \begin{array}{l}x = 1\\x = {\log _5}2\end{array} \right.\).
Giải phương trình \(\sin 3x - \frac{2}{{\sqrt 3 }}{\sin ^2}x = 2\sin x.\cos 2x\)
A. \(x = \pm \frac{\pi }{3} + k2\pi \); \(x = \frac{{2\pi }}{3} + k2\pi \) (k ∈ ℤ);
B. \(x = \pm \frac{\pi }{4} + k2\pi \); \(x = \frac{\pi }{2} + k2\pi \) (k ∈ ℤ);
C. x = kp; \(x = \frac{\pi }{3} + k2\pi \); \(x = \frac{{2\pi }}{3} + k2\pi \) (k ∈ ℤ);
D. \(x = \frac{\pi }{2} + k2\pi \); \(x = \frac{\pi }{6} + k2\pi \) (k ∈ ℤ).
Cho hàm số y = f(x) có bảng biến thiên như sau:
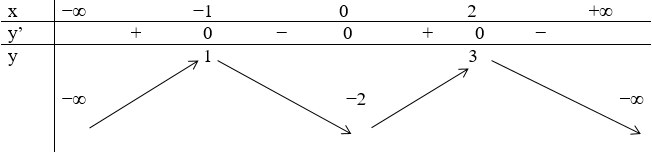
Số nghiệm thực của phương trình 2f(x) + 5 = 0 là:
A. 3;
B. 4;
C. 2;
D. 1.
Tổng các nghiệm của phương trình 4x – 3.2x+2 + 32 = 0 bằng
A. 32;
B. 3;
C. 5;
D. 12.
Tập nghiệm của bất phương trình 4x – 3.2x+2 + 32 ≤ 0 là:
A. (4; 8);
B. (2; 3);
C. [2; 3];
D. [4; 8].
Chọn mệnh đề sai trong các mệnh đề dưới đây:
A. Tồn tại khối lăng trụ đều là khối đa diện đều;
B. Tồn tại khối chóp tứ giác đều là khối đa diện đều;
C. Tồn tại khối tứ diện là khối đa diện đều;
D. Tồn tại khối hộp là khối đa diện đều.
Phương trình 5x + 251-x = 6 có tích các nghiệm là:
A. \[{\log _5}\left( {\frac{{1 - \sqrt {21} }}{2}} \right)\];
B. \({\log _5}\left( {\frac{{1 + \sqrt {21} }}{2}} \right)\);
C. 5;
D. \(5\log \left( {\frac{{1 + \sqrt {21} }}{2}} \right)\).
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I với \(AB = 2a\sqrt 3 \); BC = 2a. Biết chân đường cao H hạ từ đỉnh S xuống đáy ABCD trùng với trung điểm đoạn DI và SB hợp với mặt phẳng đáy (ABCD) một góc 60°. Khoảng cách từ D đến (SBC) tính theo a bằng
A. \(\frac{{a\sqrt {15} }}{5}\);
B. \(\frac{{2a\sqrt {15} }}{5}\);
C. \(\frac{{4a\sqrt {15} }}{5}\);
D. \(\frac{{5a\sqrt {15} }}{5}\).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mặt bên (SBC) là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng SA và BC bằng
A. \(\frac{{a\sqrt 3 }}{4}\);
B. \(\frac{{a\sqrt 2 }}{4}\);
C. \(\frac{{a\sqrt 5 }}{4}\);
D. \(\frac{{a\sqrt 3 }}{3}\).
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng 2a. Diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp ABCD là:
A. \(\frac{{\pi {a^2}\sqrt {17} }}{8}\);
B. \(\frac{{\pi {a^2}\sqrt {15} }}{4}\);
C. \(\frac{{\pi {a^2}\sqrt {17} }}{6}\);
D. \(\frac{{\pi {a^2}\sqrt {17} }}{4}\).
Gọi S là nghiệm của phương trình ln(3ex – 2) = 2x. Số tập con của S bằng
A. 0;
B. 4;
C. 1;
D. 2.
Tập nghiệm của bất phương trình ln(1 – x) < 0:
A. (−∞; 1);
B. (0; 1);
C. (0; +∞);
D. (−∞; 0).
Cho hai đường tròn bằng nhau (O; R) và (O’; R’) phân biệt. Có bao nhiêu phép vị tự biến (O; R) thành (O’; R’)?
A. 0;
B. 1;
C. 2;
D. Vô số.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, góc \(\widehat {BAD} = 60^\circ \); \(SA = SB = SD = \frac{{a\sqrt 3 }}{2}\). Gọi a là góc giữa hai mặt phẳng (SBD) và (ABCD). Mệnh đề nào sau đây đúng?
A. \(\tan a = \sqrt 5 \);
B. \(\tan a = \frac{{\sqrt 5 }}{5}\);
C. \(\tan a = \frac{{\sqrt 3 }}{2}\);
D. a = 45°.
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, CC’ = c. Độ dài đường chéo AC’ là:
A. \(AC' = \sqrt {{a^2} + {b^2} + {c^2}} \);
B. \(AC' = \sqrt { - {a^2} + {b^2} + {c^2}} \);
C. \(AC' = \sqrt {{a^2} + {b^2} - {c^2}} \);
D. \(AC' = \sqrt {{a^2} - {b^2} + {c^2}} \).
Cho x là số thực dương, số hạng không chứa x trong khai triển nhị thức \({\left( {x + \frac{2}{{\sqrt x }}} \right)^{30}}\) là:
A. 220;
B. \({2^{20}}\,.\,C_{30}^{10}\);
C. \({2^{10}}\,.\,C_{30}^{20}\);
D. \(C_{30}^{20}\).
Giá trị lớn nhất của hàm số y = x4 – 4x2 + 9 trên đoạn [−2; 3] bằng:
A. 201;
B. 9;
C. 2;
D. 54.
Giá trị lớn nhất của hàm số y = −x3 + 3x2 + 24x – 7 trên đoạn [−3; 3] bằng:
A. 65;
B. 73;
C. −25;
D. −35.
Giá trị nhỏ nhất của hàm số y = x3 + 2x2 – 7x trên đoạn [0; 4] bằng
A. −259;
B. 68;
C. 0;
D. −4.
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, \(\widehat {ABC} = 120^\circ \); ∆SAB đều và nằm trong mặt phẳng vuôn góc với mặt đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng
A. \(\frac{{a\sqrt {11} }}{6}\);
B. \(\frac{{a\sqrt {39} }}{6}\);
C. \(\frac{{a\sqrt {37} }}{6}\);
D. \(\frac{{a\sqrt {35} }}{6}\).
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (A) 4x – 3y – 7z + 3 = 0 và điểm I(1; −1; 2). Phương trình mặt phẳng đối xứng với (A) qua I là
A. (B): 4x – 3y – 7z – 3 = 0;
B. (B): 4x – 3y – 7z + 11 = 0;
C. (B): 4x – 3y – 7z – 11 = 0;
D. (B): 4x – 3y – 7z + 5 = 0.
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): mx + y – 2z – 2 = 0 và (Q): x – 3y + mz + 5 = 0. Tìm tất cả các giá trị thực của m để hai mặt phẳng đã cho vuông góc với nhau.
A. m = −2;
B. m = 3;
C. m = −3;
D. m = 2.
Tập xác định của hàm số y = log3(x2 + 2x) là
A. (−∞; −2) È (0; +∞);
B. (−∞; −2);
C. (0; +∞);
D. (−∞; −2) ∩ (0; +∞).
Cho tập hợp A = {0; 1; 2; 3; 4} và B= {x ∈ ℕ| x < 5}. Trong các kết luận sau, kết luận nào sai?
A. A∈B;
B. A ⸦ B;
C. A = B;
D. A∩B = ∅
Xếp ngẫu nhiên 10 học sinh gồm 5 nam và 5 nữ thành một hàng dọc. Xác suất để không có bất kì hai học sinh cùng giới nào đứng cạnh nhau bằng
A. \(\frac{1}{{252}}\);
B. 100%;
C. \[\frac{1}{{126}}\];
D. 50%.

