12 CÂU HỎI
Cho hàm số f(x) có bảng biến thiên như sau

Có bao nhiêu giá trị nguyên của tham số m để phương trình 3f(x2 – 4x) = m có ít nhất ba nghiệm thực phân biệt thuộc khoảng (0; +∞)?
A. 15
B. 14
C. 13
D. 12.
Trong mặt phẳng tọa độ Oxy, phương trình đường tròn (C') là ảnh của đường tròn qua (C): x2 + y2 – 2x + 4y – 1 = 0 với \(\overrightarrow v = \left( {1;2} \right)\) là:
A. \({\left( {x + 2} \right)^2} + {y^2} = \sqrt 6 \)
B. \({\left( {x - 2} \right)^2} + {y^2} = 6\)
C. x2 + y2 – 2x – 5 = 0
D. 2x2 + 2y2 – 8x + 4 = 0.
Tập xác định của hàm số y = logx là:
A. [0; +∞)
B. (0; +∞)
C. (–∞; +∞)
D. [10; +∞).
Đạo hàm của hàm số y = log(1 – x) bằng:
A. \(\frac{1}{{\left( {x - 1} \right)\ln 10}}\)
B. \(\frac{1}{{x - 1}}\)
C. \(\frac{1}{{1 - x}}\)
D. \(\frac{1}{{\left( {1 - x} \right)\ln 10}}\).
Cho x, y là các số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là sai?
A. xm . yn = (xy)m+n
B. (xy)n = xn . yn
C. xm . xn = xm+n
D. (xm)n = xmn.
Tìm tất cả các giá trị của tham số m để hàm số y = x3 + x2 + mx + 1 đồng biến trên khoảng (–∞; +∞)
A. \(m \ge \frac{4}{3}\)
B. \(m \le \frac{4}{3}\)
C. \(m \ge \frac{1}{3}\)
D. \(m \le \frac{1}{3}\).
Cho hàm số y = – x3 + 3x2 + 3mx – 1, tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)
A. m < 1
B. m ≥ 1
C. m ≤ –1
D. m ≥ –1.
Trong các mệnh đề sau, mệnh đề nào đúng?
A. ∀ n ∈ ℕ, n2 + 1 không chia hết cho 3
B. ∀ n ∈ ℝ, |x| < 3 ⇔ x < 3
C. ∀ n ∈ ℝ, (x – 1)2 ≠ x – 1
D. ∃ n ∈ ℕ, n2 + 1 chia hết cho 4.
Cho a là số thực dương, a ≠ 1 và \(P = {\log _{\sqrt[3]{a}}}{a^3}\). Mệnh đề nào dưới đây đúng?
A. P = 3
B. P = 1
C. P = 9
D. \(P = \frac{1}{3}\).
Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau:
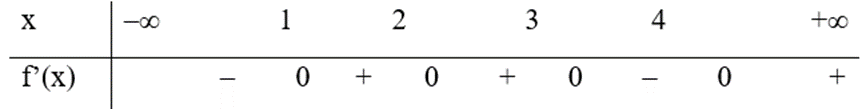
Hàm số y = 3f(x + 2) – x3 + 3x đồng biến trên khoảng nào dưới đây?
A. (1; +∞)
B. (–∞; –1)
C. (–1; 0)
D. (0; 2).
Tổng các nghiệm của phương trình 3x+1 + 31-x = 10.
A. 1
B. 3
C. –1
D. 0.
Mệnh đề nào sau đây đúng ?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có ít nhất hai vectơ cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ.

