40 CÂU HỎI
Tìm tập xác định D của hàm số y = ln(x – 1).
A. D = (−∞; −1);
B. D = (−1; + ∞);
C. D = (−∞; 1);
D. D = (1; +∞).
Tìm tập xác định D của hàm số y = ln(x – 3).
A. D = (3; +∞);
B. D = (−∞; + ∞);
C. D = (0; +∞);
D. D = (e; +∞).
Cho phương trình (m2 + 2)cos2x – 2msin2x + 1 = 0. Để phương trình có nghiệm thì giá trị thích hợp của tham số m là
A. \(\frac{{ - 1}}{2} \le m \le \frac{1}{2}\);
B. −1 ≤ m ≤ 1;
C. \( - \frac{1}{4} \le m \le \frac{1}{4}\);
D. |m| ≥ 1.
Cho hàm số f(x) = ax4 + bx3 + cx2 (a, b, c ∈ ℝ). Hàm số y = f '(x) có đồ thị như trong hình bên. Số nghiệm thực phân biệt của phương trình 2f(x) + 3 = 0.
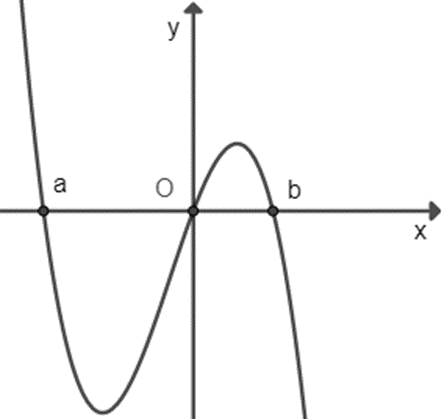
A. 4;
B. 1;
C. 2;
D. 3.
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x3 – 3(m + 2)x2 + 3(m2 + 4m)x + 1 nghịch biến trên khoảng (0; 1)?
A. 1;
B. 4;
C. 3;
D. 2.
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số \(y = \left| {\frac{1}{4}{x^4} - 14{x^2} + 48x + m - 30} \right|\) trên đoạn [0; 2] không vượt quá 30. Tổng giá trị các phân tử của tập S bằng
A. 108;
B. 136;
C. 120;
D. 210.
Gọi S là ập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số \(y = \left| {\frac{{{x^2} + mx + m}}{{}}x + 1} \right|\) trên đoạn [1; 2] bằng 2. Số phần tử của tập S là
A. 3;
B. 1;
C. 4;
D. 2.
Hình bên là đồ thị của ba hàm số y = ax, y = bx, y = cx (0 < a, b, c ≠ 1) được vẽ trên cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?
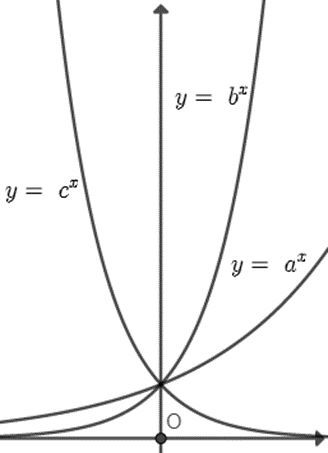
A. a > b > c;
B. c > b > a;
C. a > c > b;
D. b > a > c.
Hỏi có thể lập được bao nhiêu số tự nhiên có 4 chữ số sao cho trong mỗi số đó, chữ số hàng ngàn lớn hơn hàng trăm, chữ số hàng trăm lớn hơn hàng chục và chữ số hàng chục lớn hơn hàng đơn vị.
A. 221;
B. 209;
C. 210;
D. 215.
Tìm m để đường thẳng y = mx + 1 cắt đồ thị hàm số \(y = \frac{{x + 1}}{{x - 1}}\) tại hai điểm thuộc nhánh của đồ thị.
A. \(m \in \left( {\frac{{ - 1}}{4}; + \infty } \right)\backslash \left\{ 0 \right\}\);
B. m ∈ (0; +∞);
C. m ∈ (−∞; 0);
D. m = 0.
Cho phương trình \[4\sin \left( {x + \frac{\pi }{3}} \right).\cos \left( {x - \frac{\pi }{6}} \right) = {a^2} + \sqrt 3 \sin 2x - \cos 2x(1)\]. Gọi n là số giá trị nguyên của tham số a để phương trình (1) có nghiệm. Tính n.
A. n = 5;
B. n = 3;
C. n = 2;
D. n = 1.
Tập xác đinh của hàm số \(y = {\log _2}\left( {{2^x} - 2} \right) + {\log _{\sqrt 2 }}\frac{1}{{3 - {x^2}}}\) là
A. \(D = \left[ {1;\sqrt 3 } \right]\);
B. \(D = \left( {1;\sqrt 3 } \right)\);
C. \(D = \left( { - \sqrt 3 ;\sqrt 3 } \right)\);
D. \(D = \left( { - \sqrt 3 ;1} \right)\).
Tập xác định của hàm số y = log2(x2 – 16) + log3(3x – 1 – 9) là
A. D = (−4; 4);
B. \(D = \left( { - \infty ;4} \right) \cup \left( {4;\sqrt 2 } \right)\);
C. D = (3; 4);
D. D = (4; +∞).
Tìm số các nghiệm nguyên không âm (x; y; z) của phương trình x + y + z = 10.
A. 54;
B. 60;
C. 66;
D. 72.
Tìm m để đường thẳng y = x + m (d) cắt đồ thị hàm số \(y = \frac{{2x + 1}}{{x - 2}}(C)\) tại hai điểm phân biệt thuôc hai nhánh của đồ thị (C).
A. m ∈ ℝ;
B. \(m \in \mathbb{R}\backslash \left\{ { - \frac{1}{2}} \right\}\);
C. \(m > - \frac{1}{2}\);
D. \(m < - \frac{1}{2}\).
Cho hàm số y = f( x) có đạo hàm là hàm số y = f’(x) trên R. Biết rằng hàm số y = f ' (x – 2) + 2 có đồ thị như hình vẽ bên dưới. Hàm số y = f( x) nghịch biến trên khoảng nào?
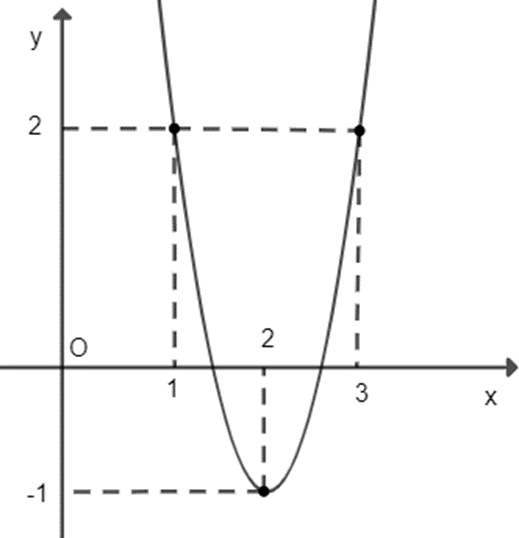
A. (−∞; 2);
B. (−1; 1);
C. \(\left( {\frac{3}{2};\frac{5}{2}} \right)\);
D. (2; +∞).
Trong các hàm số sau đây, hàm số nào xác định với mọi giá trị thực của x?
A. \[y = \sqrt {2x - 1} \];
B. y = \({\left( {2{x^2} + 1} \right)^{ - \frac{1}{3}}}\);
C. y = (1 – 2x)-3;
D. y = \({\left( {1 + 2\sqrt x } \right)^3}\).
Cho hình chop S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên (SAB) là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy; góc giữa SC và mặt phẳng đáy bằng 45°. Thể tích khối chóp S.ABCD bằng
A. \(\frac{{{a^3}\sqrt 3 }}{{12}}\);
B. \(\frac{{{a^3}\sqrt 3 }}{9}\);
C. \(\frac{{{a^3}\sqrt 5 }}{{24}}\);
D. \(\frac{{{a^3}\sqrt 5 }}{6}\).
Gọi S là tập hợp các số tự nhiên có ba chữ số (không nhất thiết khác nhau) được lập từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Chọn ngẫu nhiên một số \[\overline {abc} \] từ S. Tính xác suất để số được chọn thỏa mãn a ≤ bc.
A. \(\frac{1}{6}\);
B. \(\frac{{11}}{{60}}\);
C. \(\frac{{13}}{6}\);
D. \(\frac{9}{{11}}\).
Gọi S là tập hợp tất cả các số tự nhiên có 3 chữ số được lập từ tập hợp X = {0; 1; 2; 3; 4; 5; 6; 7}. Rút ngẫu nhiên một số thuộc tập S. Tính xác suất để rút được số mà trong số đó, chữ số đứng sau luôn lớn hơn hoặc bằng chữ số đứng trước.
A. \(\frac{2}{7}\);
B. \(\frac{{11}}{{64}}\);
C. \(\frac{3}{{16}}\);
D. \(\frac{3}{{32}}\).
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) cắt ba trục Ox, Oy, Oz tại A, B, C; trực tâm tam giác ABC là H(1; 2; 3). Phương trình của mặt phẳng (P) là:
A. x + 2y + 3z – 14 = 0;
B. x + 2y + 3z + 14 = 0;
C. \(\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1\);
D. \(\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 0\).
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) cắt ba trục Ox, Oy, Oz tại A, B, C; trực tâm tam giác ABC là H(4; 5; 6). Phương trình của mặt phẳng (P) là:
A. 4x + 5y + 6z – 77 = 0;
B. 4x + 5y + 6z + 14 = 0;
C. \(\frac{x}{4} + \frac{y}{5} + \frac{z}{6} = 1\);
D. \(\frac{x}{4} + \frac{y}{5} + \frac{z}{6} = 0\).
Ba số hạng đầu tiên theo lũy thừa tăng dần của x trong khai triển của
(1 + 2x)10 là
A. 1; 45x; 120x2;
B. 1; 4x; 4x2;
C. 1; 20x; 180x2;
D. 10; 45x; 120x2.
Cho hàm số y = (x – m)3 – 3x + m2 có đồ thị là (Cm) với m là tham số thực. Biết điểm M(a; b) là điểm cực đại của (Cm) ứng với một giá trị m thích hợp, đồng thời là điểm cực tiểu của (Cm) ứng với một giá trị khác của m. Tổng S = 2018a + 2020b bằng
A. 504;
B. −504;
C. 12504;
D. 5004.
Có hai dãy ghế đối diện nhau, mỗi dãy có ba ghế. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3 nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng
A. \(\frac{2}{5}\);
B. \(\frac{1}{{20}}\);
C. \(\frac{3}{5}\);
D. \(\frac{1}{{10}}\).
Cho hai dãy ghế đối diện nhau mỗi dãy có 5 ghế. Xếp ngẫu nhiên 10 học sinh, gồm 5 nam, 5 nữ ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ.
A. \(\frac{1}{{252}}\);
B. \(\frac{1}{{945}}\);
C. \(\frac{8}{{63}}\);
D. \(\frac{4}{{63}}\).
Cho ba điểm A, B, C cùng thuộc một mặt cầu và biết rằng \(\widehat {ACB} = 90^\circ \). Khẳng định nào sau đây là đúng?
A. AB luôn là đường kính của mặt cầu đã cho;
B. Luôn luôn có một đường tròn thuộc mặt cầu ngoại tiếp tam giác ABC;
C. Tam giác ABC vuông cân tại C;
D. AB là đường kính của một đường tròn lớn trên mặt cầu đã cho.
Cho tam thức f(x) = ax2 + bx + c, (a ≠ 0), ∆ = b2 – 4ac. Ta có f(x) ≤ 0, ∀x ∈ ℝ khi và chỉ khi:
A. \(\left\{ \begin{array}{l}a < 0\\\Delta \le 0\end{array} \right.\);
B. \(\left\{ \begin{array}{l}a \le 0\\\Delta < 0\end{array} \right.\);
C. \(\left\{ \begin{array}{l}a < 0\\\Delta \ge 0\end{array} \right.\);
D. \(\left\{ \begin{array}{l}a > 0\\\Delta \le 0\end{array} \right.\).
Cho hình bình hành ABCD có CD = 4cm, đường cao vẽ từ A đến cạnh CD bằng 3 cm. Gọi M là trung điểm của AB. DM cắt AC tại N. Tính diện tích tam giác AMN.
A. 4 cm2;
B. 10 cm2;
C. 2 cm2;
D. 1 cm2.
Cho hình bình hành ABCD, O là giao điểm của hai đường thẳng AC và BD. Vectơ chỉ có một vecto đối mà điểm đầu và điểm cuối là hai trong năm điểm A; B; C; D; O là
A. \(\overrightarrow {AB} \);
B. \(\overrightarrow {AC} \);
C. \(\overrightarrow {AD} \);
D. \(\overrightarrow {AO} \).
Cho hình bình hành ABCD, giao điểm của hai đường chéo là O. Tìm mệnh đề sai trong các mệnh đề sau:
A. \(\overrightarrow {CO} - \overrightarrow {OB} = \overrightarrow {BA} \);
B. \(\overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {DB} \);
C. \(\overrightarrow {DA} - \overrightarrow {DB} = \overrightarrow {OD} - \overrightarrow {OC} \);
D. \(\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow 0 \).
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên \(SA = a\sqrt 6 \) vuông góc với đáy (ABCD). Tính theo a diện tích mặt cầu ngoại tiếp hình chóp S.ABCD.
A. 8πa2;
B. 2 πa2;
C. 2a2;
D.\({a^2}\sqrt 2 \).
Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông cân tại B, biết SA = AC = 2a. Thể tích khối chóp S.ABC là
A. \({V_{S.ABC}} = \frac{2}{3}{a^3}\);
B. \({V_{S.ABC}} = \frac{{{a^3}}}{3}\);
C. VS.ABC = 2a3;
D. \({V_{S.ABC}} = \frac{{4{a^3}}}{3}\).
Cho hình chóp S.ABCD có đáy ABC là tam giác vuông cân tại B, cạnh AB = 3. Cạnh bên SA = 4 và vuông góc với mặt phẳng đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
A. \(\sqrt {34} \);
B. 6;
C. \(\frac{{\sqrt {34} }}{2}\);
D. \(2\sqrt 3 \).
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết AB = BC = a, AD = 2a và SA vuông góc với mặt phẳng (ABCD) và \(SA = a\sqrt 2 \). Gọi M là trung điểm AD. Khoảng cách giữa hai đường thẳng BM và SC bằng
A. \(\frac{a}{2}\);
B. a;
C. \(\frac{{a\sqrt 2 }}{2}\);
D. \(a\sqrt 2 \).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B với AC = a, biết SA⊥(ABC) và SB với đáy một góc 60. Thể tích khối chóp S.ABC là
A. \(V = \frac{{{a^3}\sqrt 6 }}{{24}}\);
B. \(V = \frac{{{a^3}\sqrt 3 }}{{24}}\);
C. \(V = \frac{{{a^3}\sqrt 6 }}{8}\);
D. \(V = \frac{{{a^3}\sqrt 6 }}{{48}}\).
Hỏi có bao nhiêu giá trị m nguyên trong đoạn [−2017; 2017] để phương trình logmx = 2log(x + 1) có nghiệm duy nhất?
A. 2017;
B. 4014;
C. 2018;
D. 4015.
Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau mà các chữ số đều là số chẵn?
A. 48;
B. 60;
C. 360;
D. 80.
Trong không gian với hệ tọa độ Oxyz , đường thẳng d đi qua điểm A(1; 2; 3) và vuông góc với mặt phẳng (P): 2x + 2y + z + 2017 = 0 có phương trình là
A. \(\frac{{x + 2}}{1} = \frac{{y + 2}}{2} = \frac{{z + 1}}{3}\);
B. \(\frac{{x - 2}}{1} = \frac{{y - 2}}{2} = \frac{{z - 1}}{3}\);
C. \(\frac{{x + 1}}{2} = \frac{{y + 2}}{2} = \frac{{z + 3}}{1}\);
D. \(\frac{{x - 1}}{2} = \frac{{y - 2}}{2} = \frac{{z - 3}}{1}\).
Tìm tất cả các giá trị của m để phương trình: x4 – 2(m – 1)x2 + 4m – 8 = 0 có 4 nghiệm phân biệt.
A. m > 2 và m ≠ 3;
B. m > 2;
C. m > 1 và m ≠ 3.
D. m > 3.

