Quiz

7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 43)

Admin13 câu hỏiToánLớp 12

Bắt đầu ngay

13 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Phương trình ax² + bx + c = 0 có nghiệm duy nhất khi và chỉ khi:

A. ∆ = 0;

B. $\{\begin{cases} a \neq 0 \\ Δ = 0 \end{cases}$ hoặc $\{\begin{cases} a = 0 \\ b \neq 0 \end{cases}$

C. a = b = 0;

D. $\{\begin{cases} a \neq 0 \\ Δ = 0 \end{cases}$ .

2. Nhiều lựa chọn

Cho tập X = {x ∈ ℕ | (x² – 4)(x – 1)(2x² – 7x + 3) = 0}. Tính tổng S các phần tử của tập hợp X.

A. S = 4;

B. $S = \frac{9}{2}$ ;

C. S = 5;

D. S = 6.

3. Nhiều lựa chọn

Tìm tập hợp các giá trị của tham số thực m để hàm số y = msinx + 7x – 5m + 3 đồng biến trên ℝ.

B. m ≤ –7

C. m ≤ –1

D. m ≥ 7.

4. Nhiều lựa chọn

Cho a là số thực dương và m,n là các số thực tùy ý. Trong các tính chất sau, tính chất nào đúng?

A. a^m + aⁿ = a^m+n.

B. a^m . aⁿ = a^m.n.

C. a^m . aⁿ = a^m+n.

D. a^m + aⁿ = a^m.n.

5. Nhiều lựa chọn

Giới hạn $\lim \frac{1^{2} + 2^{2} + 3^{2} + ... + n^{2}}{n^{3} + 2 n + 7}$ có giá trị bằng?

C. 0;

D. $\frac{1}{3}$ .

6. Nhiều lựa chọn

Trong mặt phẳng tọa độ Oxy cho A(1; 2). Tìm ảnh A’ qua phép vị tự tâm I(3; –1) tí số k = 2

A. A’(1; 5);

B. A’(–1; 5);

C. A’(3; 4);

D. A’(–5; –1).

7. Nhiều lựa chọn

Cho các hàm số $y = a^{x}; y = \log_{b} x; y = \log_{c} x$ có đồ thị như hình vẽ

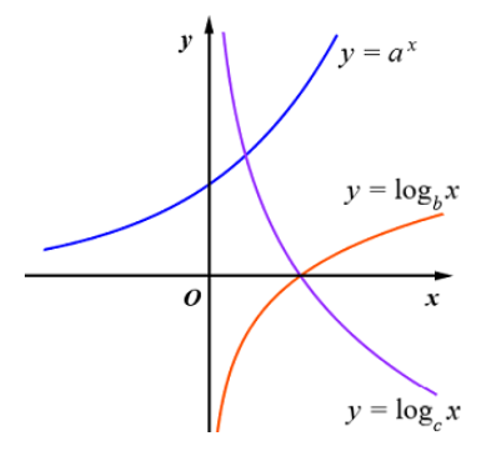
Cho các hàm số y = a^x , y = log b x , y = log c x có đồ thị như hình vẽ (ảnh 1)

Mệnh đề nào dứoi đây đúng?

A. a < c < b

B. c < a < b

C. b < c < a.

8. Nhiều lựa chọn

Cho A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật và C là tập hợp các hình vuông. Khi đó:

A. A ∩ B = C

B. A ∪ B = C

C. A \ B = C

D. B \ A = C.

9. Nhiều lựa chọn

khối chóp S.ABC có đáy ABC là tam giác vuông cân có cạnh huyền BC = a và SA vuông góc với mặt phẳng đáy. Biết góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng 45°. Thể tích của hình chóp S.ABC là:

A. $V_{S . A B C} = \frac{a^{3}}{24}$ ;

B. $V_{S . A B C} = \frac{a^{3} \sqrt{2}}{8}$ ;

C. $V_{S . A B C} = \frac{a^{3}}{8}$ ;

D. $V_{S . A B C} = \frac{a^{3} \sqrt{2}}{24}$ .

10. Nhiều lựa chọn

Cho hình lăng trụ tứ giác ABCD.A’B’C’D’ có đáy ABCD là hình vuông tâm là I và có diện tích bằng 9a2. Hình chiếu của đỉnh A’ trên mặt đáy (ABCD) là điểm H thỏa mãn $3 \vec{A H} - 2 \vec{A I} = \vec{0}$ . Biết rằng $B = a \sqrt{6}$ . Tính góc giữa mặt phẳng (ADA’) và mặt phẳng (ABCD)

A. 45°;

B. 60°;

C. 90°;

D. 30°.

11. Nhiều lựa chọn

Cho tứ diện đều ABCD có độ dài các cạnh bằng 2a. Gọi M, N lần lượt là trung điểm các cạnh AC, BC; P là trọng tâm tam giác BCD. Mặt phẳng MNP cắt tứ diện theo một thiết diện có diện tích là:

A. $\frac{a^{2} \sqrt{11}}{2}$ ;

B. $\frac{a^{2} \sqrt{2}}{4}$ ;

C. $\frac{a^{2} \sqrt{11}}{4}$ ;

D. $\frac{a^{2} \sqrt{3}}{4}$ .

12. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy. Hình chóp có bao nhiêu mặt bên là tam giác vuông?

A. 1 mặt;

B. 2 mặt;

C. 3 mặt;

D. 4 mặt.

13. Nhiều lựa chọn

Có bao nhiêu cách cho một tập hợp?