12 CÂU HỎI
Cho hình vuông ABCD cạnh bằng 2. Điểm M nằm trên đoạn thẳng AC sao cho \[{\rm{A}}M = \frac{{AC}}{4}\]. Gọi N là trung điểm của đoạn thẳng DC. Tính \(\overrightarrow {MB} .\overrightarrow {MN} \).
A. –4;
B. 0;
C. 4;
D. 16.
Cho đa giác đều 20 đỉnh. Lấy ngẫu nhiên 3 đỉnh. Tính xác suất để 3 đỉnh đó là 3 đỉnh của một tam giác vuông không cân.
A. \(\frac{2}{{35}}\);
B. \(\frac{{17}}{{114}}\);
C. \(\frac{8}{{57}}\);
D. \(\frac{8}{{19}}\).
Cho đường tròn (O; R) và điểm A nằm ngoài (O). Từ A kẻ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC. Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với (O) (E không trùng với D). Chọn câu đúng nhất:
A. Bốn điểm A, B, O, C cùng thuộc một đường tròn đường kính AC;
B. BC là đường trung trực của OA;
C. Cả A và B đều đúng;
D. Cả A và B đều sai.
Với các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số gồm 8 chữ số, trong đó chữ số 1 có mặt 3 lần, mỗi chữ số khác có mặt đúng 1 lần
A. 35 280 số;
B. 40 320 số;
C. 5 880 số;
D. 840 số.
Có bao nhiêu cách sắp xếp 3 nữ sinh, 3 nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ
A. 6;
B. 72;
C. 720;
D. 144.
Cho đường thẳng d: y = 2x + 6 cắt Ox; Oy theo thứ tự A và B. Diện tích tam giác OAB là:
A. 9;
B. 18;
C. 12;
D. 6.
Trong các hình sau : hình vuông, hình bình hành, hình chữ nhật; hình thang cân. Những hình nào có hai đường chéo bằng nhau?
A. Hình vuông, hình chữ nhật, hình thang cân;
B. Hình vuông, hình chữ nhật, hình bình hành;
C. Hình vuông, hình bình hành, hình thang cân;
D. Hình bình hành, hình chữ nhật, hình thang cân.
Cho tứ diện ABCD. Gọi P, Q lần lượt là trung điểm của AB, CD. Điểm R nằm trên cạnh BC sao cho BR = 2RC. Gọi S là giao điểm của mp (PQR) và AD. Khi đó:
A. SA = 3SD.
B. SA = 2SD.
C. SA = SD.
D. 2SA = 3SD.
Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng \(R\sqrt 3 \). Hai điểm A, B lần lượt nằm trên hai đường trong đáy sao cho góc giữa AB và trục của hình trụ bằng 30°. Khoảng cách giữa AB và trục của hình trụ bằng:
A. R;
B. \(R\sqrt 3 \);
C. \(\frac{{R\sqrt 3 }}{2}\);
D. \(\frac{{R\sqrt 3 }}{4}\).
Một người gửi ngân hàng 100 triệu đồng với kỳ hạn 3 tháng, lãi suất 2% một quý theo hình thức lãi kép. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được sau 1 năm kể từ khi bắt đầu gửi tiền gần với kết quả nào sau đây:
A. 212 triệu;
B. 210 triệu;
C. 216 triệu;
D. 220 triệu.
Phương trình x – 12 = 6 – x có nghiệm là:
A. x = 9;
B. x = –9;
C. x = 8;
D. x = –8.
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ.
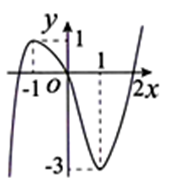Số nghiệm thực của phương trình f(2+f(ex))=1là:
A. 1;
B. 2;
C. 4;
D. 3.
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải