Quiz

7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)

Admin63 câu hỏiToánLớp 12

63 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Ba công nhân có năng suất lao động tương ứng tỉ lệ với 3, 5, 7. Tính tổng số tiền ba người được thưởng nếu biết tổng số tiền thưởng của người thứ nhất và thứ hai là 5,6 triệu.

A. 11 triệu;

B. 15 triệu;

C. 10,5 triệu;

D. 10 triệu.

2. Nhiều lựa chọn

Khẳng định nào dưới đây là khẳng định sai:

A. 12 ∈ B(3).

B. 25 ∉ B(3).

C. B(3) = {0; 3; 6; 9; 12; ... }.

D. B(3) = {3; 6; 9; 12; ... }.

3. Nhiều lựa chọn

Cho dãy số (u_n) biết $u_{n} = \frac{1}{n + 1}, \forall n \geq 1$ . Ba số hạng đầu tiên của dãy số đó là:

A. $\frac{1}{2}; \frac{1}{3}; \frac{1}{4}$

B. $1; \frac{1}{2}; \frac{1}{3}$

C. $\frac{1}{2}; \frac{1}{4}; \frac{1}{6}$

D. $1; \frac{1}{3}; \frac{1}{5}$

4. Nhiều lựa chọn

Cho đường thẳng a không vuông góc với mặt phẳng (P). Khi đó, góc giữa đường thẳng a và mặt phẳng (P) là góc giữa:

A. a và hình chiếu vuông góc của a lên (P).

B. a và một đường thẳng bất kì cắt (P).

C. a và đường vuông góc với (P).

D. a và một đường thẳng bất kì nằm trong (P).

5. Nhiều lựa chọn

Cho hai mặt phẳng (P) và (Q) song với nhau. Đường thẳng d nằm trong mặt phẳng (P). Khi đó đường thẳng d có đặc điểm gì?

A. d song song với (Q).

B. d cắt (Q).

C. d nằm trong (Q).

D. d có thể cắt (Q) hoặc nằm trong (Q).

6. Nhiều lựa chọn

Cho hàm số f(x) = 3 + cosx. Khẳng định nào sau đây đúng:

A. $\int f (x) d x = 3 x + \sin x + C$

B. $\int f (x) d x = 3 x - \cos x + C$

C. $\int f (x) d x = 3 x - \sin x + C$

D. $\int f (x) d x = 3 x + \cos x + C$

7. Nhiều lựa chọn

Cho hàm số f(x) = e^x + 2. Khẳng định nào sau đây đúng?

A. $\int f (x) d x = e^{x} + C$

B. $\int f (x) d x = e^{x} + 2 x + C$

C. $\int f (x) d x = e^{x} - 2 x + C$

D. $\int f (x) d x = e^{x - 2} + C$

8. Nhiều lựa chọn

Cho hàm số $y = \frac{x - 2}{x + 1}$ . Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng (−∞; −1).

B. Hàm số đồng biến trên khoảng (−∞; −1) và (−1; +∞).

C. Hàm số đồng biến trên khoảng (−∞; +∞).

D. Hàm số nghịch biến trên khoảng (−1; +∞).

9. Nhiều lựa chọn

Cho hình hộp ABCD.A'B'C'D'. Đường thẳng BC song song với mặt phẳng nào sau đây?

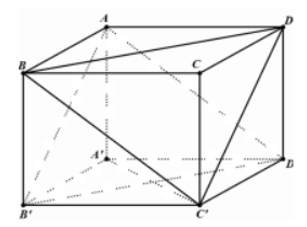
Cho hình hộp ABCD.A'B'C'D'. Đường thẳng BC song song với mặt phẳng nào sau đây? A. (DD'A'). B. (DCC'). C. (A'B'B). D. (ABD). (ảnh 1)

A. (DD'A').

B. (DCC').

C. (A'B'B).

D. (ABD).

10. Nhiều lựa chọn

Cho mặt phẳng (P) tiếp xúc với mặt cầu S(I; R). Gọi d là khoảng cách từ I đến (P). Khẳng định nào dưới đây đúng?

A. d < R.

B. d > R.

C. d = R.

D. d = 0.

11. Nhiều lựa chọn

Đồ thị của hàm số y = 3^x đi qua điểm nào sau đây?

A. M(– 1; 3).

B. N(1; 3).

C. P(0; 2).

D. Q(– 1; 3).

12. Nhiều lựa chọn

Góc lượng giác nào sau đây có cùng điểm cuối với góc $\frac{7 π}{4}$ ?

A. $- \frac{π}{4}$

B. $\frac{π}{4}$

C. $\frac{3 π}{4}$

D. $\frac{13 π}{4}$

13. Nhiều lựa chọn

Gọi M₁, M₂ là hai điểm lần lượt biểu diễn cho các số phức z₁, z₂ là nghiệm của phương trình z² + 2z + 4 = 0. Tính số đo góc $\hat{M_{1} O M_{2}}$ .

A. $\hat{M_{1} O M_{2}} = 120 °$ .

B. $\hat{M_{1} O M_{2}} = 90 °$ .

C. $\hat{M_{1} O M_{2}} = 60 °$ .

D. $\hat{M_{1} O M_{2}} = 150 °$ .

14. Nhiều lựa chọn

Trong không gian, hai đường thẳng cùng song song với đường thẳng thứ ba thì hai đường thẳng đó:

A. Hoặc song song hoặc trùng nhau.

B. Chéo nhau.

C. Trùng nhau.

D. Song song.

15. Nhiều lựa chọn

Hai đường thẳng song song với nhau nếu chúng cùng cắt một đường thẳng thứ ba và trong các góc tạo thành có:

A. Hai góc so le trong bù nhau.

B. Hai góc đồng vị phụ nhau.

C. Hai góc trong cùng phía bù nhau.

D. Hai góc đồng vị bù nhau.

16. Nhiều lựa chọn

Hai tập hợp nào dưới đây không bằng nhau?

A. $A = \{x | x = \frac{1}{2^{k}}, k \in ℤ, x \geq \frac{1}{8}\}$ và $B = \{\frac{1}{2}; \frac{1}{4}; \frac{1}{8}\}$ .

B. A = {3;9;27;81} và B = {3ⁿ|n ∈ ℕ, 1 ≤ n ≤ 4}.

C. A = {x ∈ ℤ|– 2 < x ≤ 3} và B = {– 1; 0; 1; 2; 3}.

D. A = {x ∈ ℕ| x < 5} và B = {0; 1; 2; 3; 4}.

17. Nhiều lựa chọn

Hàm số nào dưới đây không là nguyên hàm của hàm số f(x) = sin²x?

A. $F (x) = \frac{1}{2} (x - \frac{\sin 2 x}{2}) + C$

B. $F (x) = \frac{1}{4} (2 x - \sin x \cos x) + C$

C. $F (x) = \frac{1}{2} (x - \sin x \cos x) + C$

D. $F (x) = \frac{1}{4} (2 x - \sin 2 x) + C$

18. Nhiều lựa chọn

Hàm số y = –3x² + x – 2 nghịch biến trên khoảng nào sau đây?

A. $(\frac{1}{6}; + \infty)$

B. $(- \infty; - \frac{1}{6})$

C. $(\frac{- 1}{6}; + \infty)$

D. $(- \infty; \frac{1}{6})$

19. Nhiều lựa chọn

Hình chóp lục giác đều có bao nhiêu đỉnh?

A. 4

B. 6

C. 5

D. 7

20. Nhiều lựa chọn

Hình chóp lục giác đều có bao nhiêu đỉnh?

A. 4

B. 6

C. 5

D. 7

21. Nhiều lựa chọn

Hình lăng trụ có đáy là hình chữ nhật có bao nhiêu mặt là hình chữ nhật?

A. 4

B. 5

C. 6

D. 3

22. Nhiều lựa chọn

Trong không gian với hệ tọa độ Oxyz, cho điểm A(− 2; 3; 4). Khoảng cách từ điểm A đến trục Ox là:

A. 4

B. 3

C. 5

D. 2

23. Nhiều lựa chọn

Khối đa diện lồi đều có số mặt nhiều nhất là

A. 12

B. 30

C. 8

D. 20

24. Nhiều lựa chọn

Tổng độ dài l của tất cả các cạnh của một tứ diện đều cạnh a.

A. l = 4a.

B. l = 6a.

C. l = 6.

D. l = 4.

25. Nhiều lựa chọn

Cho tam giác ABC vuông tại A. Biết cosB = 0,8. Khi đó cotB bằng:

A. $\frac{4}{3}$

B. $\frac{3}{5}$

C. $\frac{5}{3}$

D. $\frac{3}{4}$

26. Nhiều lựa chọn

Tìm tập giá trị của hàm số y = ln(3 – x).

A. (e; +∞).

B. (0; +∞).

C. ℝ.

D. [e; +∞).

27. Nhiều lựa chọn

Tập nghiệm của bất phương trình 2^2x < 8 là

A. $(- \infty; \frac{3}{2})$

B. $(\frac{3}{2}; + \infty)$

C. (– ∞; 2).

D. $(0; \frac{3}{2})$

28. Nhiều lựa chọn

Tập nghiệm của phương trình 2^x+1 = 5 có bao nhiêu phần tử?

A. 3

B. 2

C. 0

D. 1

29. Nhiều lựa chọn

Trong không gian, cho hai đường thẳng song song a và b. Mệnh đề nào sau đây đúng?

A. Có đúng một mặt phẳng đi qua cả hai đường thẳng a và b.

B. Có đúng hai mặt phẳng đi qua cả hai đường thẳng a và b.

C. Có vô số mặt phẳng đi qua cả hai đường thẳng a và b.

D. Không tồn tại mặt phẳng đi qua cả hai đường thẳng a và b.

30. Nhiều lựa chọn

Trong không gian cho tứ diện ABCD. Hai đường thẳng nào sau đây chéo nhau?

A. BC và AC.

B. AD và BC.

C. BD và CD.

D. BC và AB.

31. Nhiều lựa chọn

Trong không gian Oxyz, cho mặt cầu (S): (x – 1)² + (y + 2)² + (z + 3)² = 4. Tâm của (S) có tọa độ là:

A. (– 1; 2; 3).

B. (2; – 4; – 6).

C. (– 2; 4; 6)

D. (1; – 2; – 3).

32. Nhiều lựa chọn

Trong không gian Oxyz, góc giữa trục Oz và mặt phẳng (Oxy) là:

A. 30°.

B. 60°.

C. 90°.

D. 45°.

33. Nhiều lựa chọn

Trong không gian Oxyz, góc giữa trục Ox và mặt phẳng (Oyz) là:

A. 30°.

B. 60°.

C. 90°.

D. 45°.

34. Nhiều lựa chọn

Trong không gian Oxyz, mặt phẳng nào dưới đây song song với mặt phẳng (Oxy)?

A. (α): z + 1 = 0.

B. (β): x + z + 1 = 0.

C. (γ): y + 1 = 0.

D. (φ): x + 1 = 0.

35. Nhiều lựa chọn

Mặt phẳng (P): 3x + 5y – z – 2 = 0 cắt trục Oz tại điểm có tọa độ:

A. (0; 0; −2).

B. (3; 5; −1).

C. (3; 5; 0).

D. (0; 0; 2).

36. Nhiều lựa chọn

Trong không gian Oxyz, trục Oz có một vectơ chỉ phương là?

A. (0;0;1)

B. (1;0;1)

C. (1;0;0)

D. (0;1;0)

37. Nhiều lựa chọn

Mệnh đề nào sau đây có mệnh đề phủ định sai:

A. ∃x ∈ ℝ: x² + 4x + 5 = 0.

B. ∀x ∈ ℝ: x² ≥ x.

C. ∃x ∈ ℚ: x² = 3.

D. ∃x ∈ ℝ: x² – 3x + 2 = 0.

38. Nhiều lựa chọn

Một miếng tôn hình chữ nhật có chiều dài 98cm, chiều rộng 30cm được uốn lại thành mặt xung quanh của một thùng đựng nước (chiều cao thùng nước bằng với chiều rộng miếng tôn). Biết rằng chỗ mối ghép mất 2cm. Hỏi thùng đựng được tối đa bao nhiêu lít nước?

A. 22 lít.

B. 24 lít.

C. 26 lít.

D. 28 lít.

39. Nhiều lựa chọn

Phương trình đường tròn tâm I(0; 2), bán kính R = 5 là

A. x² + (y – 2)² = 25.

B. (x – 2)² + y² = 25.

C. x² + (y – 2)² = 5.

D. x² + (y + 2)² = 25.

40. Nhiều lựa chọn

Trong không gian với hệ trục toạ độ Oxyz. Biết A, B, C là số thực khác 0, mặt phẳng chứa trục Oz có phương trình là:

A. Ax + Bz + C = 0.

B. Ax + By = 0.

C. By + Az + C = 0.

D. Ax + By + C = 0.

41. Nhiều lựa chọn

Cho hàm số y = f(x) có bảng biến thiên như sau:

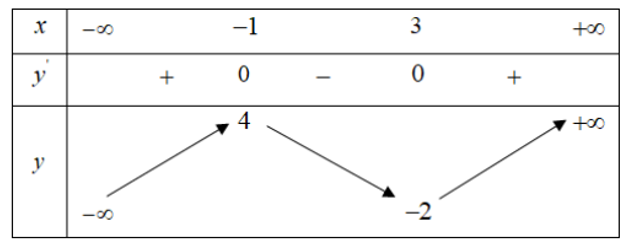
Cho hàm số y = f(x) có bảng biến thiên như sau: Số nghiệm của phương trình f(x) – 2 = 0 là: A. 0. B. 3. C. 1. D. 2. (ảnh 1)

Số nghiệm của phương trình f(x) – 2 = 0 là:

A. 0

B. 3

C. 1

D. 2

42. Nhiều lựa chọn

Số tập con gồm 3 phần tử của tập hợp gồm 8 phần tử bằng:

A. $A_{8}^{3}$

B. 3⁸ – 1.

C. $C_{8}^{3}$

D. 3⁸.

43. Nhiều lựa chọn

Với ba điểm O, A, B tùy ý. Khẳng định nào dưới đây luôn đúng?

A. $\vec{O A} - \vec{O B} = \vec{B A}$

B. $\vec{O A} - \vec{O B} = \vec{A B}$

C. $\vec{O A} + \vec{O B} = \vec{A B}$

D. $\vec{O A} + \vec{O B} = \vec{B A}$

44. Nhiều lựa chọn

Trong các mệnh đề sau, mệnh đề nào không phải là định lý:

A. ∃x ∈ ℕ, x² chia hết cho 3 ⇒ x chia hết cho 3.

B. ∃x ∈ ℕ, x² chia hết cho 6 ⇒ x chia hết cho 3.

C. ∀x ∈ ℕ, x² chia hết cho 9 ⇒ x chia hết cho 9.

D. ∃x ∈ ℕ, x chia hết cho 4 và 6 ⇒ x chia hết cho 12

45. Nhiều lựa chọn

Trong không gian Oxyz, mặt phẳng (P): $\frac{x}{3} + \frac{y}{5} + \frac{z}{2} = 1$ cắt trục Oy tại điểm có tọa độ là?

A. (0;5;0).

B. (0;3;0).

C. (0; – 1;0).

D. (0;2;0).

46. Nhiều lựa chọn

Một thủ kho có một chùm chìa khóa gồm 9 chiếc trông giống hệt nhau trong đó chỉ có 1 chiếc mở được kho nhưng anh ta không biết là chiếc nào. Anh ta thử ngẫu nhiên từng chìa khóa một, chiếc nào được thử thì không thử lại. Tính xác suất anh ta mở được cửa ở lần thử thứ 3?

A. $\frac{1}{6}$

B. $\frac{2}{7}$

C. $\frac{14}{81}$

D. $\frac{7}{81}$

47. Nhiều lựa chọn

Trên khoảng (0; +∞), đạo hàm của hàm số y = lnx là:

A. $\frac{1}{x}$

B. x

C. xlnx – x.

D. $\frac{1}{x^{2}}$

48. Nhiều lựa chọn

Trong không gian oxyz, mặt phẳng nào dưới đây không đi qua gốc tọa độ:

A) 3x + y – z = 0

B) 5x + 3y – 3z = 0

C) x + 7y + z = 0

D) –x – y + 20 = 0

49. Nhiều lựa chọn

Số tổ hợp chập 2 của 5 phần tử bằng:

A)5

B)10

C)15

D)20

50. Nhiều lựa chọn

Chọn đáp án không đúng:

Hàm số $y = \sin (2 x - \frac{π}{4})$ đồng biến trên khoảng nào dưới đây

A. $(- \frac{π}{8}; \frac{3 π}{8})$

B. $(- \frac{π}{4}; \frac{3 π}{4})$

C. $(- \frac{π}{2}; \frac{π}{2})$

D. $(- \frac{π}{4}; \frac{π}{4})$

51. Nhiều lựa chọn

Số các chỉnh hợp chập 3 của 12 phần tử là

A. $C_{12}^{3}$

B. $\frac{12!}{3!}$

C. $\frac{12!}{9!}$

D. 12! – 3!

52. Nhiều lựa chọn

Trên bản đồ tỉ lệ 1/50.000, 1 cm tương đương với độ dài bao nhiêu ngoài thực địa?

A. 500 cm trên thực địa

B. 50 cm trên thực địa

C. 5 km trên thực địa

D. 0,5 km trên thực địa

53. Nhiều lựa chọn

Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên $S A = a \sqrt{2}$ và SA vuông góc với mặt phẳng đáy, tam giác SBD là tam giác đều. Thể tích của khối chóp S.ABCD bằng

A. $\frac{2 a^{3} \sqrt{2}}{3}$

B. $2 a^{3} \sqrt{2}$

C. $\frac{a^{3} \sqrt{2}}{3}$

D. $a^{3} \sqrt{2}$

54. Nhiều lựa chọn

Số nghiệm thực của phương trình 3x² + 1 = 9 là

A. 1

B. 2

C. 3

D. 4

55. Nhiều lựa chọn

Góc giữa hai trục ox và oz bằng

A) 90⁰

B) 45⁰

C) 60⁰

D) 30⁰

56. Nhiều lựa chọn

Cho hình nón có bán kính đáy bằng a và chiều cao bằng căn 3 độ dài đường sinh của hình nón đã cho bằng

A. $\sqrt{2} a$

B. 2a

C. $\sqrt{10} a$

D, 4a

57. Nhiều lựa chọn

Số chỉnh hợp chập 3 của 6 phần tử bằng

A. $C_{6}^{3}$

B. $\frac{6!}{3!}$

C. $\frac{6!}{2}$

D. 6! – 3!

58. Nhiều lựa chọn

Giá trị của $\lim_{x \to + \infty} (x - 1)$ là

A) 0

B) 1

C) +∞

D) –∞

59. Nhiều lựa chọn

Số dư trong phép chia 53 chia 5 là

A. 1

B. 2

C. 3

D. 4

60. Nhiều lựa chọn

Cho $\frac{7 π}{4} < α < 2 π$ . Nhận xét nào sau đây là đúng?

A) tan α > 0

B) cot α > 0

C) cos α > 0

D) sin α > 0

61. Nhiều lựa chọn

Cho tập hợp M gồm 4 phần tử, số tập hợp con gồm 3 phần tử của M là

A. 1

B. 2

C. 3

D. 4

62. Nhiều lựa chọn

Trong không gian Oxyz, cho ba điểm A(1, 0, 0), B(0; –2, 0), C(0, 0, 3). Phương trình mặt phẳng đi qua ba điểm A, B,C là

A. 6x – 3y + 2z = 0

B. 6x + 3y + 2z – 6 = 0

C. 6x + 3y + 2z + 6 = 0

D. 6x – 3y + 2z – 6 = 0

63. Nhiều lựa chọn

Cho hình chóp đều S.ABCD có độ dài tất cả các cạnh bằng a. Góc giữa hai đường thẳng SB và CD bằng

A. $30 °$

B. $45 °$

C, $60 °$

D. $90 °$

Gợi ý cho bạn

QuizToán - Tốt nghiệp THPT

Trắc nghiệm củng cố

2 câu hỏi3 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi5 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi28 lượt thi

QuizToán - Lớp 12

10 bài tập Xác định các yếu tố cơ bản của đường thẳng trong không gian có lời giải

10 câu hỏi16 lượt thi

QuizToán - Lớp 12

10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải

10 câu hỏi14 lượt thi

QuizToán - Lớp 12

10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Khoảng cách từ một điểm đến một mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình mặt phẳng đi qua 1 điểm kèm điều kiện song song với mặt phẳng khác có lời giải

10 câu hỏi13 lượt thi

Facebook Youtube