7 CÂU HỎI
Cho tam giác ABC cân tại A có góc A bằng 40°. Đường trung trực của AB cắt AB tại H, cắt BC tại D. Số đo góc ADB là
A. 50°;
B. 30°;
C. 40°;
D. Không đủ dữ kiện để xác định.
Cho hình vẽ. So sánh đúng là
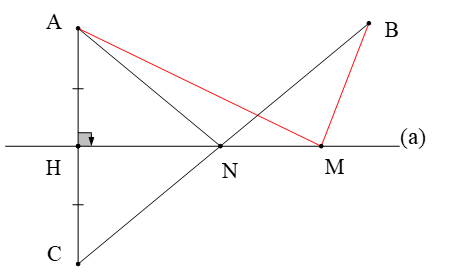
A. BC > MA + MB;
B. BC = MA + MB;
C. BC < MA + MB;
D. BC > NA + NB.
Cho ∆MAB, ∆NAB, ∆PAB là ba tam giác cân chung đáy AB. Khẳng định đúng là
A. M, N, P trùng nhau;
B. M, N, P thẳng hàng;
C. M, N, P không thẳng hàng;
D. Cả A, B và C đều sai.
Cho ∆ABC cân tại A, trung tuyến AM, đường trung trực của AC cắt AM ở D. Khẳng định đúng là
A. DA = DB;
B. DA = DM;
C. DA = DC;
D. Cả A và C đều đúng.
Đường trung trực của đoạn AB cắt AB tại H. Hai điểm M, N là hai điểm trên đường trung trực đó (N nằm giữa M và H).Gọi N’ là giao điểm của AN và BM. Khẳng định sai là
A. MN là tia phân giác ;
B. BN’ > AN’;
C. Tam giác MAB cân tại M;
D. NA = NB.
Cho tam giác có một đường phân giác đồng thời là đường trung trực ứng với cùng một cạnh thì tam giác đó là tam giác
A. Tam giác vuông;
B. Tam giác cân;
C. Tam giác nhọn;
D. Không tồn tại tam giác như vậy.
Trong ∆ABC hai đường trung trực của hai cạnh AB và AC cắt nhau tại D nằm trên cạnh C.Khẳng định đúng nhất là
A. D là trung điểm của BC;
B. ;
C. Tam giác ABC vuông tại A;
D. Cả A, B và C đều đúng.
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải