67 CÂU HỎI
Căn bậc hai của 9 là:
A. 3
B. \(\sqrt 3 \)
C. 3 và -3
D. -3
\[\frac{1}{9}\] và \[ - \frac{1}{9}\]là căn bậc hai của số nào trong các số dưới đây:
A. \(\frac{1}{3}\)
B. \(\)\(\frac{1}{{81}}\)
C. \( - \frac{1}{3}\)
D. \(\frac{1}{{18}}\)
Căn bậc hai số học của 4 là:
A. 2 và -2
B. 2
C. -2
D. 16
Căn bậc ba của -125 là:
A. 5
B. \(\)-5
C. 25
D. 5 và -5
Điều kiện xác định của biểu thức \[\sqrt[3]{a}\] là:
A. \(a > 0\)
B. \(\)\(a \ge 0\)
C. \(a \in \mathbb{Z}\)
D. \(a \in \mathbb{R}\)
Điều kiện xác định của biểu thức \[\sqrt a \] là:
A. \(a > 0\)
B. \(\)\(a \ge 0\)
C. \(a \in \mathbb{Z}\)
D. \(a \in \mathbb{R}\)
Sử dụng máy tính cầm tay để tìm giá trị của \[\sqrt[3]{{ - 0,125}}\]
A. -0,5
B. \(\)0,5
C. -0,125 < 0 nên không tính được
D. 0,25
Khoanh vào khẳng định sai trong các khẳng định dưới đây:
A. \[\sqrt[3]{{ - 11,35}} > \sqrt[3]{{ - 13,12}}\]
B. \(\)Nếu a < b thì \[\sqrt[3]{a} < \sqrt[3]{b}\](a, b là số thực)
C. Nếu a > b thì \[\sqrt a > \sqrt b \](a,b )
D. \[3 > \sqrt[3]{{27\frac{1}{4}}}\]
Khoanh vào khẳng định đúng trong các khẳng định dưới đây:
A. \[\sqrt {\frac{4}{3}} > \sqrt {\frac{3}{4}} \]
B. \[\sqrt {0,48} > 0,7\]
C. \[(2 + \sqrt 3 )(2 - \sqrt 3 ) = - 1\]
D. Số âm không có căn bậc 3
Tìm phát biểu đúng trong các phát biểu sau:
A. Mỗi số dương có đúng một căn bậc hai
B. Số âm và số dương đều có căn bậc 2
C. Số âm và số dương đều có căn bậc 3
D. Căn bậc ba của một số âm là số dương
Tìm phát biểu sai trong các phát biểu sau:
A. \[ - 10 < \sqrt[3]{{ - 999}}\]
B. \[(\sqrt[3]{2} + 1)[{(\sqrt[3]{2})^2} - \sqrt[3]{2} + 1] = - 3\]
C. \[(\sqrt 7 - 1)(\sqrt 7 + 1) = 6\]
D. Căn bậc hai số học của 16 là 4
Tìm nghiệm của phương trình sau: \[{x^2} = 25\]
A. \(x = 5\)
B. \(x = 5;x = - 5\)
C. \(x = - 5\)
D. \(x = 25\)
\[\frac{3}{4}\] là căn bậc hai số học của số nào dưới đây:
A. \[\frac{9}{{16}}\]
B. \[ - \frac{9}{{16}}\]
C. \[\frac{6}{8}\]
D. \[ - \frac{6}{8}\]
Khẳng định nào sau đây sai:
A. \[3 > 2\sqrt 2 \]
B. \[11 < \sqrt {99} \]
C. Căn hai số học của của
D. Luôn tồn tại căn bậc hai một số luôn là số dương của một số thực dương
Định luật thứ ba của Kepler về sự chuyển động của các hành tinh trong hệ Mặt Trời cho biết khoảng cách trung bình d ( triệu dặm ) từ một hành tinh quay xung quanh Mặt Trời được tính bởi công thức: d= \[\sqrt[3]{{6{t^2}}}\] với t( ngày Trái Đất ) là thời gian hành tinh đó quay quanh Mặt trời đúng một vòng. Hỏi Trái Đất cách Mặt Trời bao xa biết Trái Đất ngay một vòng quanh Mặt Trời trong khoảng 365 ngày ( làm tròn kết quả đến chữ số thập phân thứ nhất )
A. 92,1
B. 92,08
C. 92,8
D. 92,008
Một hình vuông có diện tích 0,0144 cm2. Cạnh của hình vuông đó dài:
A. 0,12 m
B. 0,06 cm
C. 0,12 cm
D. 0,06 m
Kết quả thu gọn của biểu thức \[(\sqrt[3]{3} + 1)(\sqrt[3]{9} + \sqrt[3]{3} + 1)\] là:
A. \[\sqrt[3]{3}\]
B. 1
C. 9
D. 4
Gọi S là tập các giá trị nguyên của x thỏa mãn biểu thức \(\sqrt x < 7\). Số phần tử của tập S là:
A. 48
B. 35
C. 49
D. 50
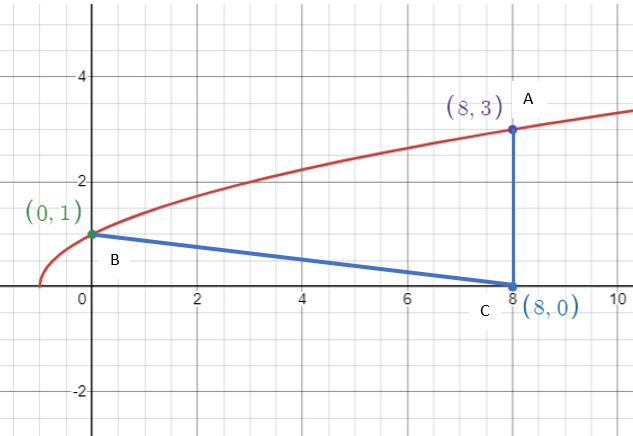
Điểm A (x,y) thuộc đồ thị hàm số trên sao cho tam giác COB có diện tích là 4 ( biết C là chân đường vuông góc kẻ từ A xuống trục Ox). Giá trị của y là:
A. 2
B. 3
C. 4
D. 5
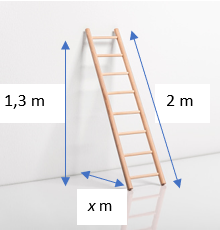
Một cái thang dựa vào tường như hình bên dưới. Tìm khoảng cách từ chân thang tới góc tường biết thang dài 2m và tường cao 1,3m
A. 2,13 m
B. 1,98 m
C. 1,5 m
D. 1,3 m
Tìm số \(x\) không âm thỏa mãn \(\sqrt x = 6\)
A. \(36\)
B. \(6\)
C. \(12\)
D. \(3\)
Kết quả của phép tính\(\sqrt {36} .\sqrt {64} \) là
A. \(36\)
B. \(6\)
C. \(8\)
D. \(48\)
Kết quả của phép tính \(\frac{{\sqrt {99} }}{{\sqrt {11} }}\) là
A. \(9\)
B. \(11\)
C. \(3\)
D. \(\sqrt 3 \)
Trục căn thức ở mẫu của \(\frac{{15}}{{\sqrt 5 }}\) được kết quả là
A. \(3\)
B. \(5\)
C. \(\sqrt 5 \)
D. \(3\sqrt 5 \)
Cho \(M = 5\) và \(N = \frac{{\sqrt {50} }}{2}\). Khẳng định nào sau đây đúng.
A. \(M < N\)
B. \(M + 2 = N\)
C. \(M = N\)
D. \(M > N\)
Giá trị của biểu thức \(\sqrt {125} - \sqrt {80} + \sqrt {20} \) là
A. \(11\sqrt 5 \)
B. \(15\)
C. \(3\sqrt 5 \)
D. \(6\sqrt 5 \)
Khử mẫu của biểu thức \(\sqrt {\frac{3}{{125}}} \) sẽ được kết quả là
A. \[\frac{{\sqrt {15} }}{{25}}\]
B. \[\frac{{\sqrt {25} }}{{15}}\]
C. \[\frac{{\sqrt 5 }}{{25}}\]
D. \[\frac{{\sqrt 5 }}{{15}}\]
Trục căn thức ở mẫu của \(\frac{2}{{\sqrt 3 - 1}}\)được kết quả là
A. \(2\left( {\sqrt 3 + 1} \right)\)
B. \(2\left( {\sqrt 3 - 1} \right)\)
C. \(\sqrt 3 + 1\)
D. \(\sqrt 3 - 1\)
Trục căn thức ở mẫu của \(\frac{3}{{\sqrt {10} + \sqrt 7 }}\) được kết quả là
A. \(\sqrt {10} - \sqrt 7 \)
B. \(\sqrt {10} + \sqrt 7 \)
C. \(3\left( {\sqrt {10} - \sqrt 7 } \right)\)
D. \(3\left( {\sqrt {10} + \sqrt 7 } \right)\)
Giá trị của biểu thức \(4\sqrt {\frac{{25}}{{16}}} + 5\sqrt {\frac{9}{{25}}} \) là
A. \(9\)
B. \(8\)
C. \(7\)
D. \(\frac{5}{4}\)
Kết quả của phép tính \(\sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} + 1\) là
A. \(\sqrt 3 - 2\)
B. \(\sqrt 3 \)
C. \(2 - \sqrt 3 \)
D. \( - \sqrt 3 \)
Kết quả của phép tính \(\sqrt {9 - 4\sqrt[{}]{5}} \) là
A. \(3 - 2\sqrt 5 \)
B. \(2 - \sqrt 5 \)
C. \(\sqrt 5 - 2\)
D. Kết quả khác
Cho biểu thức \(A = \frac{{\sqrt {45} + \sqrt 5 }}{{\sqrt {125} - \sqrt {80} }}\). Giá trị của \(3A\) là
A. \(12\)
B. \(9\)
C. \(15\)
D. \(8\)
Biểu thức \(\left( {\sqrt 5 + 3\sqrt 2 } \right)\left( {2\sqrt 5 + \sqrt 2 } \right) - \left( {\sqrt 2 + 3\sqrt 5 } \right)\left( {2\sqrt 2 + \sqrt 5 } \right)\) có kết quả là
A. \[ - 1\]
B. \(1\)
C. \( - 2\)
D. \( - 3\)
Giá trị của biểu thức \(N = \sqrt {9 - 4\sqrt 5 } + \sqrt {9 + 4\sqrt 5 } \) bằng
A. \(N = 4\)
B. \(N = \sqrt 5 \)
C. \(N = \sqrt 5 + 4\)
D. \(N = 2\sqrt 5 \)
Cho biểu thức \(A = \sqrt {4 + \sqrt {4 + \sqrt {4 + ......} } } \)( có vô hạn số \(\sqrt 4 \)). Giá trị của biểu thức \(A\) là
A. \(\frac{{1 - \sqrt {17} }}{2}\)
B. \( - \frac{{1 + \sqrt {17} }}{2}\)
C. \(\frac{{ - 1 + \sqrt {17} }}{2}\)
D. \(\frac{{1 + \sqrt {17} }}{2}\)
Tốc độ của một chiếc cano và độ dài đường sóng nước để lại sau đuôi của nó được cho bởi công thức \(v = 5\sqrt I \), trong đó \(I\) là độ dài đường nước sau đuôi cano (mét), \(v\) là vận tốc của cano (m/giây). Khi cano chạy với vận tốc \(54\,\,km/h\) thì đường sóng nước để lại sau đuôi chiếc cano dài bao nhiêu mét?
A. \(5\)
B. \(5\sqrt 3 \)
C. \(9\)
D. \(3\sqrt 5 \)
Kết quả của phép tính\(\sqrt {49{a^2}} + 3a\) với \(a \ge 0\) là
A. \[10a\]
B. \[4a\]
C. \[ - 4a\]
D. \[52a\]
Biểu thức\(2{b^2}\sqrt {\frac{{{a^4}}}{{4{b^2}}}} \) với \(b > 0\) bằng:
A. \[\frac{{{a^2}}}{2}\]
B. \[{a^2}b\]
C. \[ - {a^2}b\]
D. \[\frac{{{a^2}{b^2}}}{{{b^2}}}\]
Điều kiện xác định của biểu thức \(Z = \sqrt[3]{{3 - x}} + \frac{1}{{\sqrt {x - 1} }}\) là:
A. \(1 \le x \le 3\)
B. \(1 < x \le 3\)
C. \(x > 1\)
D. \(x \ge 1\)
Điều kiện xác định của biểu thức \(K = \sqrt { - {x^2} + 5x - 6} - \frac{1}{{2x + 5}}\) là:
A. \(2 \le x \le 3\)
B. \(\left\{ \begin{array}{l}x \ge - 2\\x \ne \frac{5}{2}\end{array} \right.\)
C. \(\left\{ \begin{array}{l}2 \le x \le 3\\x \ne - \frac{5}{2}\end{array} \right.\)
D. \(x \le 0\)
Với giá trị nào của x thì biểu thức \(\sqrt {x - 2\sqrt {x - 1} } \) có nghĩa?
A. \(x \le 0\)
B. \(x \ge 1,x \ne 0\)
C. \(x \ge 0,x \ne 1\)
D. \(x \ge 1\)
Giá trị của biểu thức \(\sqrt {9{a^2}({b^2} + 4 - 4b)} \) khi \(a = 2\) và \(b = - \sqrt 3 \) bằng giá trị nào sau đây?
A. \(3\left( {2 + \sqrt 3 } \right)\)
B. \(6\left( {2 - \sqrt 3 } \right)\)
C. \(6\left( {2 + \sqrt 3 } \right)\)
D. \(3\left( {2 - \sqrt 3 } \right)\)
Biểu thức \(\frac{{ - 3}}{{10 - 5x}}\) có căn bậc hai khi
A. \(x < 2\)
B. \(x \le 2\)
C. \(x > 2\)
D. \(x \ge 2\)
Tìm điều kiện để biểu thức \(\sqrt {\left( {5\sqrt x + 7} \right)\left( {5\sqrt x - 7} \right)} \) có nghĩa?
A. \(x \le - \frac{5}{7}\)
B. \(x \ge 0\)
C. \(x \ge \frac{{49}}{{25}}\)
D. \(x \ge - \frac{5}{7}\)
Tìm điều kiện xác định biểu thức \(\frac{{\sqrt {{x^2} - 5x + 6} }}{{{x^2} - 4}}\) có nghĩa?
A. \(x < 2,x \ge 3\)
B. \(x \le 2,x \ge 3,x \ne - 2\)
C. \(x < 2,x > 3,x \ne - 2\)
D. \(x < 2,x \ge 3,x \ne - 2\)
Biểu thức \(\sqrt {\left| {x - 1} \right| - 3} \) có nghĩa khi:
A. \(\left[ \begin{array}{l}x \le - 2\\x \ge 4\end{array} \right.\)
B. \(x \le - 2\)
C. \( - 2 \le x \le 4\)
D. \(x \ge 4\)
Rút gọn biểu thức\(B = \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} + \sqrt 3 \)
A. \[2\sqrt 3 \]
B. \[ - 2\sqrt 3 \]
C. \[ - 2\]
D. \[2\]
Biểu thức \(\sqrt {{{(3 - 2x)}^2}} \) bằng:
A. \(3 - 2x\).
B. \(2x - 3\).
C. \(\left| {2x - 3} \right|\).
D. \(3 - 2x\) và \(2x - 3\)
Rút gọn biểu thức sau: \(A = \sqrt {64{a^2}} + 2a\)với \(a \ge 0\)
A. \(A = 20a\)
B. \(A = 68a\)
C. \(A = 10a\)
D. \(A = 8a\)
Rút gọn biểu thức \[\sqrt {\frac{{{x^2}}}{{{y^4}}}} \]với \(x > 0;\,y \ne 0\), ta được
A. \[ - \frac{{{x^2}}}{{{y^4}}}\].
B. \[\frac{{{x^2}}}{{{y^4}}}\].
C. \[ - \frac{x}{{{y^2}}}\].
D. \[\frac{x}{{{y^2}}}\].
Rút gọn biểu thức \[\frac{{\sqrt {32{a^2}} }}{{\sqrt 2 }}\] với \[a < \,0\] được kết quả là
A. \[16{a^2}\].
B. \[4a\].
C. \[ - 4a\].
D. \[ - 16{a^2}\].
Khử mẫu của biểu thức \(\sqrt {\frac{3}{{125}}} \) sẽ được kết quả là
A. \[\frac{{\sqrt {15} }}{{25}}\].
B. \[\frac{{\sqrt {25} }}{{15}}\].
C. \[\frac{{\sqrt 5 }}{{25}}\].
D. \[\frac{{\sqrt 5 }}{{15}}\].
Trục căn thức ở mẫu biểu thức \(\frac{5}{{2\sqrt 3 }}\) có kết quả là
A. \(\frac{{5\sqrt 3 }}{6}\).
B. \(\frac{{3\sqrt 5 }}{6}\).
C. \(\frac{{\sqrt 3 }}{6}\).
D. \(\frac{{3\sqrt 3 }}{6}\).
Trục căn thức ở mẫu biểu thức \(\frac{6}{{\sqrt 5 - \sqrt 3 }}\) có kết quả là
A. \(3\).
B. \(3.\left( {\sqrt 5 - \sqrt 3 } \right)\).
C. \(3.\left( {\sqrt 5 + \sqrt 3 } \right)\).
D. \( - 3\).
Rút gọn biểu thức \(\sqrt {0,36{{(a - 1)}^2}} \) với \(a < 1\) ta được kết quả là
A. \(0,6(a - 1)\)
B. \(0,36(1 - a)\).
C. \(0,6(1 - a)\).
D. \(0,36a\).
Biểu thức \(\sqrt {25\left( {{x^2} - 4x + 4} \right)} \) khi \(x \ge 2\) bằng
A. \(5\left( {x - 2} \right)\).
B. \( - 5\left( {x - 2} \right)\).
C. \(5\left( {x + 2} \right)\).
D. \( - 5\left( {x + 2} \right)\).
Với \(y < 0\), kết quả của phép tính \(2y.\sqrt {\frac{{{x^4}}}{{4{y^2}}}} \) là
A. \( - {x^2}\).
B. \({x^2}\).
C. \(\frac{{{x^2}}}{{2y}}\).
D. \(\frac{{ - {x^2}}}{{2y}}\).
Rút gọn biểu thức \[\frac{{\sqrt {63{y^3}} }}{{\sqrt {7y} }}\] với \[y\, > \,0\] được kết quả là
A. \[3{y^2}\].
B. \[9y\].
C. \[3y\].
D. \[ - 3y\].
Khử mẫu biểu thức sau \[xy\sqrt {\frac{4}{{{x^2}{y^2}}}} \] với \[x > 0;y > 0\] ta được kết quả là
A. \[4\].
B. \[\sqrt { - xy} \].
C. \[\sqrt 2 \].
D. \[2\].
Trục căn thức ở mẫu biểu thức \[\frac{3}{{6 + \sqrt {3a} }}\] với \(a \ge 0;a \ne 12\) ta được kết quả là
A. \[\frac{{6 + \sqrt {3a} }}{{12 + a}}\].
B. \[\frac{{6 - \sqrt {3a} }}{{12 + a}}\].
C. \[\frac{{6 + \sqrt {3a} }}{{12 - a}}\].
D. \[\frac{{6 - \sqrt {3a} }}{{12 - a}}\].
Giá trị của biểu thức \[\sqrt {4{x^2}\left( {{y^2} + 6y + 9} \right)} \]tại \(x = 2;\,y = - \sqrt 7 \) là
A. \(4\sqrt 7 - 3\).
B. \[4\left( {\sqrt 7 - 3} \right)\].
C. \[4\left( {3 - \sqrt 7 } \right)\].
D. \[8\left( {\sqrt 7 - 3} \right)\].
Nghiệm của phương trình \(\sqrt {25\left( {x - 1} \right)} = 10\) là
A. \(x = 2,5\).
B. \(x = 0,4\).
C. \(x = 4\).
D. \(x = 5\).
Rút gọn biểu thức \[\sqrt {27x} - \sqrt {48x} + 4\sqrt {75x} + \sqrt {243x} \] với \(x \ge 0\) ta được
A. \[40\sqrt {3x} \].
B. \[28\sqrt {3x} \].
C. \[39\sqrt x \].
D. \[28\sqrt x \].
Cho . Nghiệm của phương trình \(2Ax + 3 = 0\) là
A. \(x = 1\).
B. \(x = - 1\).
C. \(x = 2\).
D. \(x = - 2\).
Cho biểu thức \(P = \left( {\frac{{2x + 1}}{{\sqrt {{x^3}} - 1}} - \frac{1}{{\sqrt x - 1}}} \right):\left( {1 - \frac{{x + 4}}{{x + \sqrt x + 1}}} \right)\). Tìm các giá trị nguyên của \(x\) để \(P\) nhận giá trị nguyên dương.
A. \(x = 1;\;x = 36\).
B. \(x = - 1;\;x = 36\).
C. \(x = 4;\;x = 6\).
D. \(x = 16;\;x = 36\).
Cho biểu thức \(C = \left( {\frac{{\sqrt x }}{{\sqrt x - 1}} + \frac{2}{{x - \sqrt x }}} \right):\frac{1}{{\sqrt x - 1}}\) với \(x > 0;\;x \ne 1\). Tìm giá trị nhỏ nhất của \(C\).
A. \(C = 1\).
B. \(C = \sqrt 2 \).
C. \(C = 2\).
D. \(C = 2\sqrt 2 \).

