63 CÂU HỎI
Cho tam giác \(ABC\)vuông tại A có góc nhọn \(C\) bằng \(\alpha \) Khi đó\(\cos \alpha \) bằng
A. \(\cos \alpha = \frac{{AB}}{{BC}}\)
B. \(\cos \alpha = \frac{{AC}}{{BC}}\)
C. \(\cos \alpha = \frac{{AB}}{{AC}}\)
D. \(\cos \alpha = \frac{{AC}}{{AB}}\)
Cho \(\alpha \)là góc nhọn bất kì. Khẳng định đúng là
A. \(\cos \alpha = \frac{1}{{\tan \alpha }}\)
B. \(\sin \alpha = \frac{1}{{\tan \alpha }}\)
C. \(\cot \alpha = \frac{1}{{\tan \alpha }}\)
D. \(\cot \alpha = \frac{1}{{\sin \alpha }}\)
Cho tam giác vuông có góc \(\alpha \) là góc nhọn. Khẳng định sai là
A. Tỉ số giữa cạnh đối và cạnh huyền được gọi là cosin của góc \(\alpha \), kí hiệu cos \(\alpha \)
B. Tỉ số giữa cạnh kề và cạnh huyền được gọi là cosin của góc \(\alpha \), kí hiệu cos \(\alpha \)
C. Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \(\alpha \), kí hiệu tan \(\alpha \)
D. Tỉ số giữa cạnh kề và cạnh đối được gọi là cosin của góc \(\alpha \), kí hiệu cot \(\alpha \)
Cho \(\alpha \)là góc nhọn bất kì có \(\tan \alpha = \frac{1}{7}\), khi đó \(\cot \alpha \)bằng:
A. \(\cot \alpha = \frac{1}{7}\)
B. \(\cot \alpha = \frac{{ - 1}}{7}\)
C. \(\cot \alpha = 7\)
D. \(\cot \alpha = - 7\)
Cho \(\alpha ;\,\,\beta \) là hai góc nhọn phụ nhau, khi đó:
A. \(\sin \alpha = \,\cos \beta \)
B. \(\sin \alpha = \,\cot \beta \)
C. \(\sin \alpha = \,\tan \beta \)
D. \(\cos \alpha = \,\cot \beta \)
Tỉ số lượng giác của góc nào lớn hơn tỉ số lượng giác của góc \(45^\circ \)?
A. \(\sin 25^\circ \)
B. \(\cos 25^\circ \)
C. \(\cos 30^\circ \)
D. \(\tan 50^\circ \)
Tỉ số lượng giác của góc nào nhỏ hơn tỉ số lượng giác của góc \(45^\circ \)?
A. \(\cos 55^\circ \)
B. \(\sin 75^\circ \)
C. \(\cot 30^\circ \)
D. \(\tan 40^\circ \)
Cho tam giác \(ABC\)vuông tại \(A.\). Khi đó, trong các khẳng định sau, khẳng định nào đúng?
A. \(\frac{{AB}}{{AC}} = \frac{{\cos C}}{{\cos B}}\)
B. \(\sin B = \cos C\)
C. \(\sin B = \tan C\)
D. \(\tan B = \cos C\)
Cho tam giác \(ABC\)vuông tại C có\[AC = 1cm,{\rm{ }}BC = 2cm\]. Tính tỉ số lượng giác \[{\rm{sinB, cosB}}\]
A. \(\sin B = \frac{1}{{\sqrt 3 }};\cos B = \frac{{2\sqrt 3 }}{3}\)
B. \(\sin B = \frac{{\sqrt 5 }}{5};\cos B = \frac{{2\sqrt 5 }}{5}\)
C. \(\sin B = \frac{1}{2};\cos B = \frac{2}{{\sqrt 5 }}\)
D. \(\sin B = \frac{{2\sqrt 5 }}{5};\cos B = \frac{{\sqrt 5 }}{5}\)
Cho tam giác \(ABC\)vuông tại \(C\)có\(AC = 1,2cm,\,BC = 0,9cm\).Tính các tỉ số lượng giác \[{\rm{sinB, cosB}}\]
A. \(\sin B = 0,6;\,\,\cos B = 0,8\)
B. \(\sin B = 0,8;\,\,\cos B = 0,6\)
C. \(\sin B = 0,4;\,\,\cos B = 0,8\)
D. \(\sin B = 0,6;\,\,\cos B = 0,4\)
Cho tam giác \[ABC,\]vuông tại A có \(AB = 3;\,AC = 4\).Chọn khẳng định sai?
A. \(\sin B = \frac{{AC}}{{BC}} = \frac{4}{5}\)
B. \(\cos B = \frac{{AB}}{{BC}} = \frac{3}{5}\)
C. \(\tan B = \frac{{AC}}{{AB}} = \frac{4}{3}\)
D. \(\cot B = \frac{{AC}}{{BC}} = \frac{4}{5}\)
Cho tam giác \(ABC\)vuông tại \(A\), có \(\widehat B = 34^\circ \). Khi đó:
A. \(\sin B = \sin 34^\circ = \frac{{AB}}{{BC}}\)
B. \(\cos B = \cos 34^\circ = \frac{{AB}}{{BC}}\)
C. \(\tan B = \tan 34^\circ = \frac{{AC}}{{BC}}\)
D. \(\cot B = \cot 34^\circ = \frac{{AC}}{{AB}}\)
Dùng MTBT, tính giá trị của biểu thức ( làm tròn đến chữ số thập phân thứ ba )
A. \(M = 0,15\)
B. \(M = 0,154\)
C. \(M = 0,23\)
D. \(M = 0,228\)
Dùng MTBT, tìm độ đo của góc nhọn \(x\)( làm tròn đến phút) của \(\cot x = 1,254\)
A. \(x \approx 51^\circ 25'\)
B. \(x \approx 51^\circ 52'\)
C. \(x \approx 38^\circ 34'\)
D. \(x \approx 38^\circ 43'\)
Không dùng MTBT, tính giá trị của biểu thức \(K = \tan 76^\circ - \cot 14^\circ \)
A. \(K = 0\)
B. \(K = 1\)
C. \(K = 2\)
D. \(K = 3\)
Không dùng MTBT, tính giá trị của biểu thức \(I = \frac{{\sin 32^\circ }}{{\cos 58^\circ }}\)
A. \(I = 4\)
B. \(I = 2\)
C. \(I = 1\)
D. \(I = 3\)
Một cái thang dài 6m, được đặt tạo với mặt đất một góc \(60^\circ \), vậy chân thang cách tường bao nhiêu mét?
A. \(3{\rm{m}}\)
B. \(3,2\;{\rm{m}}\)
C. \(7,8{\rm{m}}\)
D. \(0,4m\)
Một mảnh vườn hình chữ nhật có chiều dài là \(30m\), góc giữa đường chéo và chiều dài của mảnh vườn là \(30^\circ \). Tính chiều rộng của mảnh vườn hình chữ nhật đó.
A. \(20\sqrt 3 m\)
B. \(10\sqrt 3 m\)
C. \(10\sqrt {6\,} m\)
D. \(20\sqrt {6\,} m\)
Cho hình vẽ. Hệ thức nào dưới đây đúng?
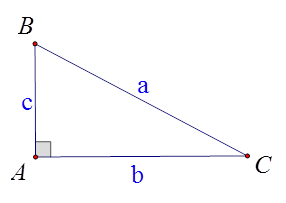
A. \(b = a\,\sin B\).
B. \(b = a\,\sin C\).
C. \(b = a\,\cos B\).
D. \(b = a\,\tan B\).
Cho hình vẽ.Hệ thức nào dưới đây đúng?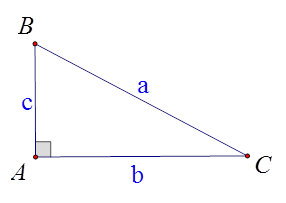
A. \(c = a\,\sin B\).
B. \(c = a\,\sin C\).
C. \(c = a\,\cos B\).
D. \(c = a\,\tan B\).
Cho hình vẽ. Hãy chọn hệ thức đúng trong các hệ thức sau: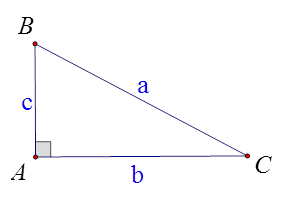
A. \(c = a\,\sin B\).
B. \(b = a\,\tan C\).
C. \(b = c\tan B\).
D. \(c = a\,\tan B\).
Cho hình vẽ. Hệ hệ thức nào dưới đây đúng?
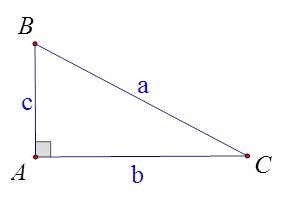
A. \(c = b\cot B\).
B. \(b = a\,\tan C\).
C. \(b = c\tan C\).
D. \(c = a\,\tan B\).
Cho hình vẽ. Hệ thức nào dưới đây đúng?
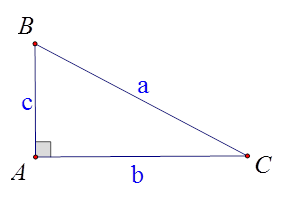
A. \(a = b\sin B\).
B. \(a = \frac{b}{{\sin B}}\).
C. \(a = \frac{b}{{\sin C}}\).
D. \(a = \,\frac{b}{{{\rm{cos}}B}}\).
Cho hình vẽ. Hệ thức nào dưới đây đúng?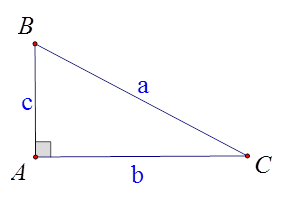
A. \(a = \frac{c}{{\sin B}}\).
B. \(a = \frac{c}{{\sin C}}\).
C. \(a = \frac{c}{{\tan C}}\).
D. \(a = \,\frac{b}{{\cot B}}\).
Cho hình vẽ bên. Hệ thức nào dưới đây đúng?
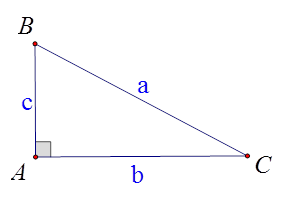
A. \(a = \frac{c}{{\sin B}}\).
B. \(a = \frac{b}{{\sin C}}\).
C. \(a = \frac{c}{{\tan C}}\).
D. \(c = \,\frac{b}{{\cot C}}\).
Cho hình vẽ. Hệ thức nào dưới đây là sai?
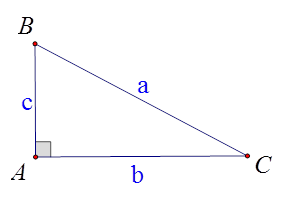
A. \(a = \frac{b}{{\sin B}}\).
B. \(a = \frac{c}{{\sin C}}\).
C. \(a = \frac{b}{{cosC}}\).
D. \(a = \,\frac{b}{{\cot C}}\).
Cho tam giác \(MNP\) vuông tại \(N\). Hệ thức nào sau đây là đúng?
A. \(MN = MP.\sin P\).
B. \(MN = MP.\cos P\).
C. \(MN = MP.\tan P\).
D. \(MN = MP.\cot P\).
Cho tam giác \(MNP\) vuông tại \(N\). Hệ thức nào sau đây là đúng?
A. \(NP = MP.\cos P\).
B. \(NP = MN.\cos P\).
C. \(NP = MN.\tan P\).
D. \(NP = MP.\cot P\).
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,AC = b,AB = c\). Chọn khẳng định sai?
A. \(b = a.\sin B = a.\cos C\).
B. \(a = c.\tan B = c.\cot C\).
C. \({a^2} = {b^2} + {c^2}\).
D. \(c = a.\sin C = a.\cos B\).
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,AC = b,AB = c,\widehat {ABC} = 50^\circ \). Chọn khẳng định đúng?
A. \(b = c.\sin 50^\circ \).
B. \(b = a.\tan 50^\circ \).
C. \(b = c.\cot 50^\circ \).
D. \(c = b.cot50^\circ \).
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 10\,cm,\widehat C = 30^\circ \). Tính \(AB;BC\).
A. \(AB = \frac{{5\sqrt 3 }}{3};BC = \frac{{20\sqrt 3 }}{3}\).
B. \(AB = \frac{{10\sqrt 3 }}{3};BC = \frac{{14\sqrt 3 }}{3}\).
C. \(AB = \frac{{10\sqrt 3 }}{3};BC = 20\sqrt 3 \).
D. \(AB = \frac{{10\sqrt 3 }}{3};BC = \frac{{20\sqrt 3 }}{3}\).
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 20\,cm,\widehat C = 60^\circ \). Tính \(AB;BC\).

A. \(AB = 20\sqrt 3 ;BC = 40\).
B. \(AB = 20\sqrt 3 ;BC = 40\sqrt 3 \).
C. \(AB = 20;BC = 40\).
D. \(AB = 20;BC = 20\sqrt 3 \).
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 12\,cm;\widehat B = 40^\circ \). Tính \(AC;\widehat C\) (làm tròn đến chữ số thập phân thứ hai)

A. \(AC \approx 7,71;\widehat C = 40^\circ \).
B. \(AC \approx 7,72;\widehat C = 50^\circ \).
C. \(AC \approx 7,71;\widehat C = 50^\circ \).
D. \(AC \approx 7,73;\widehat C = 50^\circ \).
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 15\,cm,\widehat B = 55^\circ \). Tính \(AC;\widehat C\) (làm tròn đến chữ số thập phân thứ hai).

A. \(AC \approx 12,29;\widehat C = 45^\circ \).
B. \(AC \approx 12,29;\widehat C = 35^\circ \).
C. \(AC \approx 12,2;\widehat C = 35^\circ \).
D. \(AC \approx 12,92;\widehat C = 40^\circ \).
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 15\,cm,AB = 12\,cm\). Tính \(AC;\widehat B\).

A. \(AC = 8(cm);\widehat B \approx 36^\circ 52'\).
B. \(AC = 9(cm);\widehat B \approx 36^\circ 52'\).
C. \(AC = 9(cm);\widehat B \approx 37^\circ 52'\).
D. \(AC = 9(cm);\widehat B \approx 36^\circ 55'\).
Cho tam giác \(ABC\) vuông tại \(A\) có . Tính \(AC;\widehat B\) (làm tròn đến độ).
A. \(AC = 22;\widehat C \approx 67^\circ \).
B. \(AC = 24;\widehat C \approx 66^\circ \).
C. \(AC = 24;\widehat C \approx 67^\circ \).
D. \(AC = 24;\widehat C \approx 68^\circ \).
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 7cm,AB = 5cm\). Tính \(BC;\widehat C\).
A. \(BC = \sqrt {74} (cm);\widehat C \approx 35^\circ 32'\).
B. \(BC = \sqrt {74} (cm);\widehat C \approx 36^\circ 32'\).
C. \(BC = \sqrt {74} (cm);\widehat C \approx 35^\circ 33'\).
D. \(BC = \sqrt {75} (cm);\widehat C \approx 35^\circ 32'\).
Cho tam giác \[ABC\]có \(AB = 16,AB = 14\) và . Tính \(BC\).
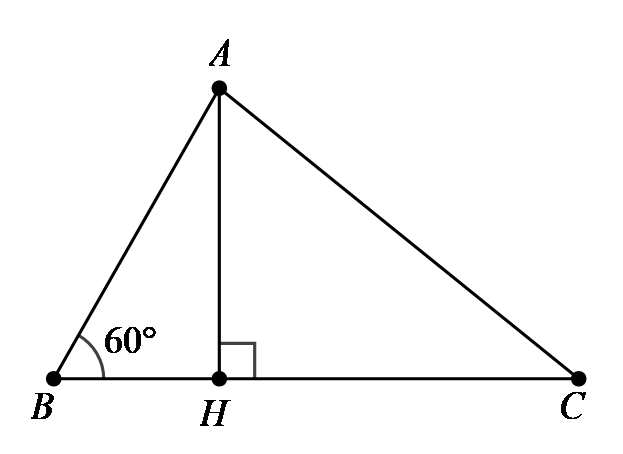
A. \(BC = 10\).
B. \(BC = 11\).
C. \(BC = 9\).
D. \(BC = 12\).
Cho tam giác \(ABC\) có \(AB = 12,AC = 15\) và . Tính \(BC\).
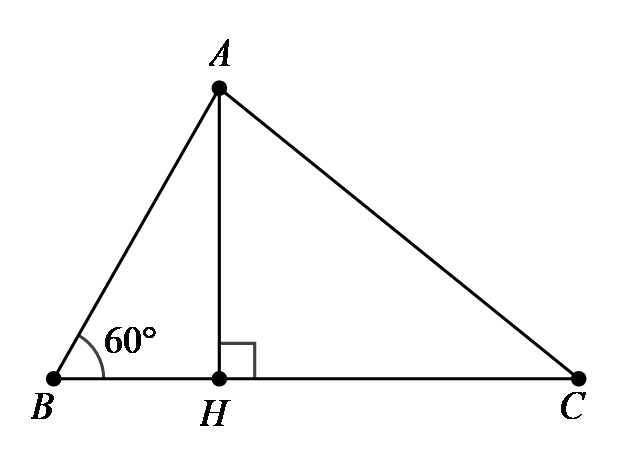
A. \(BC = 3\sqrt 3 + 6\).
B. \(BC = 3\sqrt {13} + 6\).
C. \(BC = 9\).
D. \(BC = 6\).
Cho tam giác \(ABC\) có \(AB = 4,\,\,AC = 3,5,\,\,\widehat A = 40^\circ \). Diện tích tam giác \(ABC\)là
A. \(5\)(đvdt).
B. \(4,4\)(đvdt).
C. \(3\)(đvdt).
D. \(3,5\)(đvdt).
Cho tam giác \(ABC\) có \(BC = 9cm,\widehat {ABC} = 50^\circ \) và \[\widehat {ACB} = 35^\circ \]. Gọi \(N\) là chân đường vuông góc hạ từ \(A\) xuống cạnh\(BC\). Độ dài \(AN\) gần nhất với giá trị nào dưới đây?

A. \(5\).
B. \(4\).
C. \(2\).
D. \(3\).
Cho tam giác \(ABC\) có \(BC = 9cm,\widehat {ABC} = 50^\circ \) và \[\widehat {ACB} = 35^\circ \]. Gọi \(N\) là chân đường vuông góc hạ từ \(A\) xuống cạnh\(BC\). Độ dài \(AC\) gần nhất với giá trị nào dưới đây?

A. \(7\).
B. \(6\).
C. \(5\).
D. \(4\).
Cho hình thang \(ABCD\) có\(\widehat A = \widehat D = 90^\circ \), \(\widehat C = 50^\circ \). Biết \(AB = 2,\,AD = 1,2\).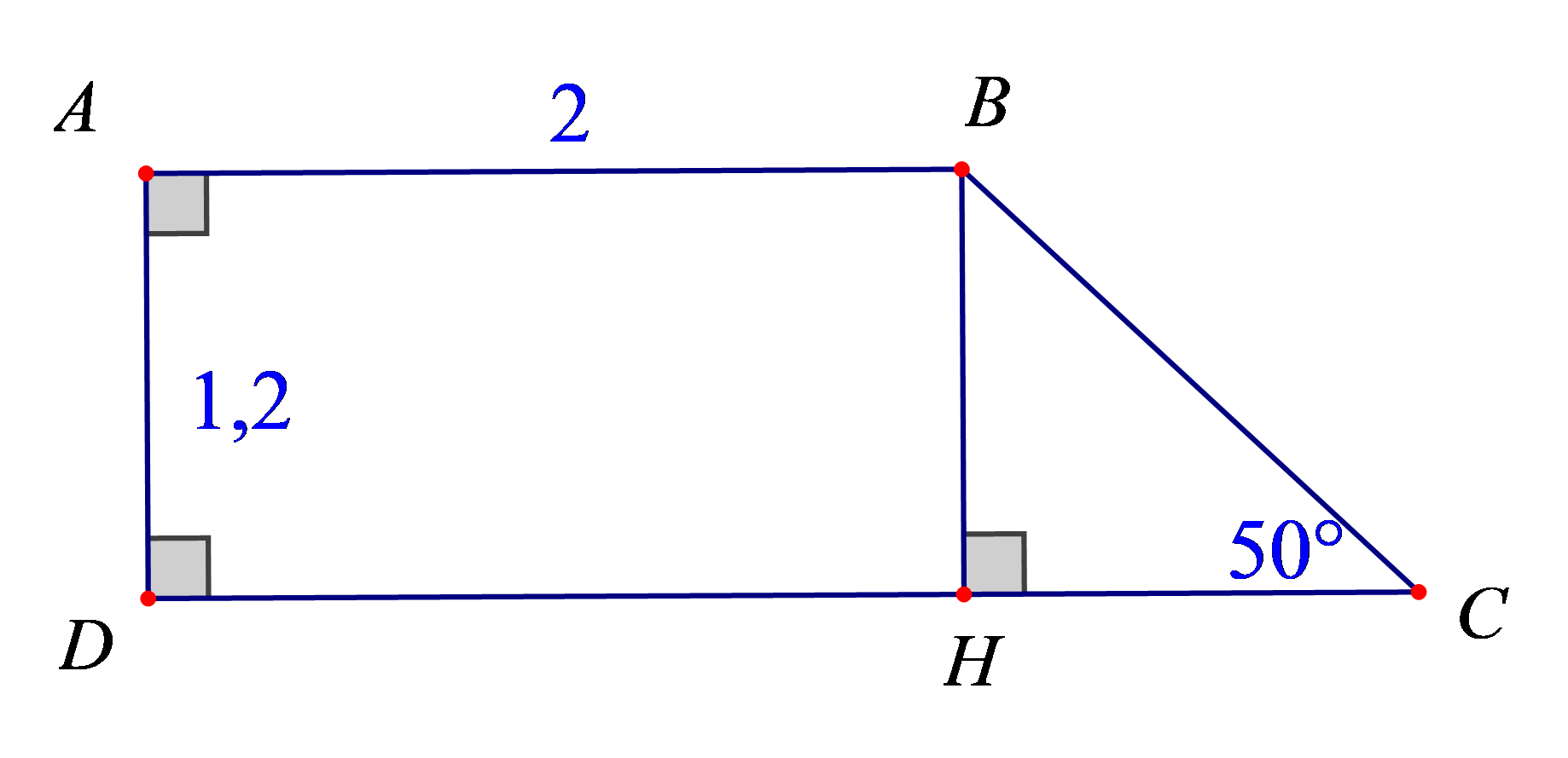
Diện tích hình thang\(ABCD\) là
A. \(3\)(đvdt).
B. \(2\)(đvdt).
C. \(4\)(đvdt).
D. \(5\)(đvdt).
Tại một thời điểm trong ngày, các tia nắng mặt trời tạo với phương ngang một góc bằng \[35^\circ \], khi đó cột \[AH\] có bóng trên mặt đất là đoạn \[BH\]dài \[7,2\,\,{\rm{m}}\]. Trong các hệ thức sau, hệ thức nào đúng khi tính chiều cao của cột \[AH\]?

A. \[AH = 7,2.\cos 35^\circ \].
B. \[AH = 7,2.\sin 35^\circ \].
C. \[AH = 7,2.\tan 35^\circ \].
D. \[AH = 7,2.\cot 55^\circ \].
Một chiếc thang có chiều dài từ chân lên đến nấc thang cuối là \[5\,\,{\rm{m}}\] được đặt vào thân cây cau như hình vẽ dưới đây, người ta đo được khoảng cách từ chân thang đến gốc cây cau là \[2,5\,\,{\rm{m}}\]. Tính góc \[\alpha \] tạo bởi thang và thân cây cau (làm tròn kết quả đến độ).
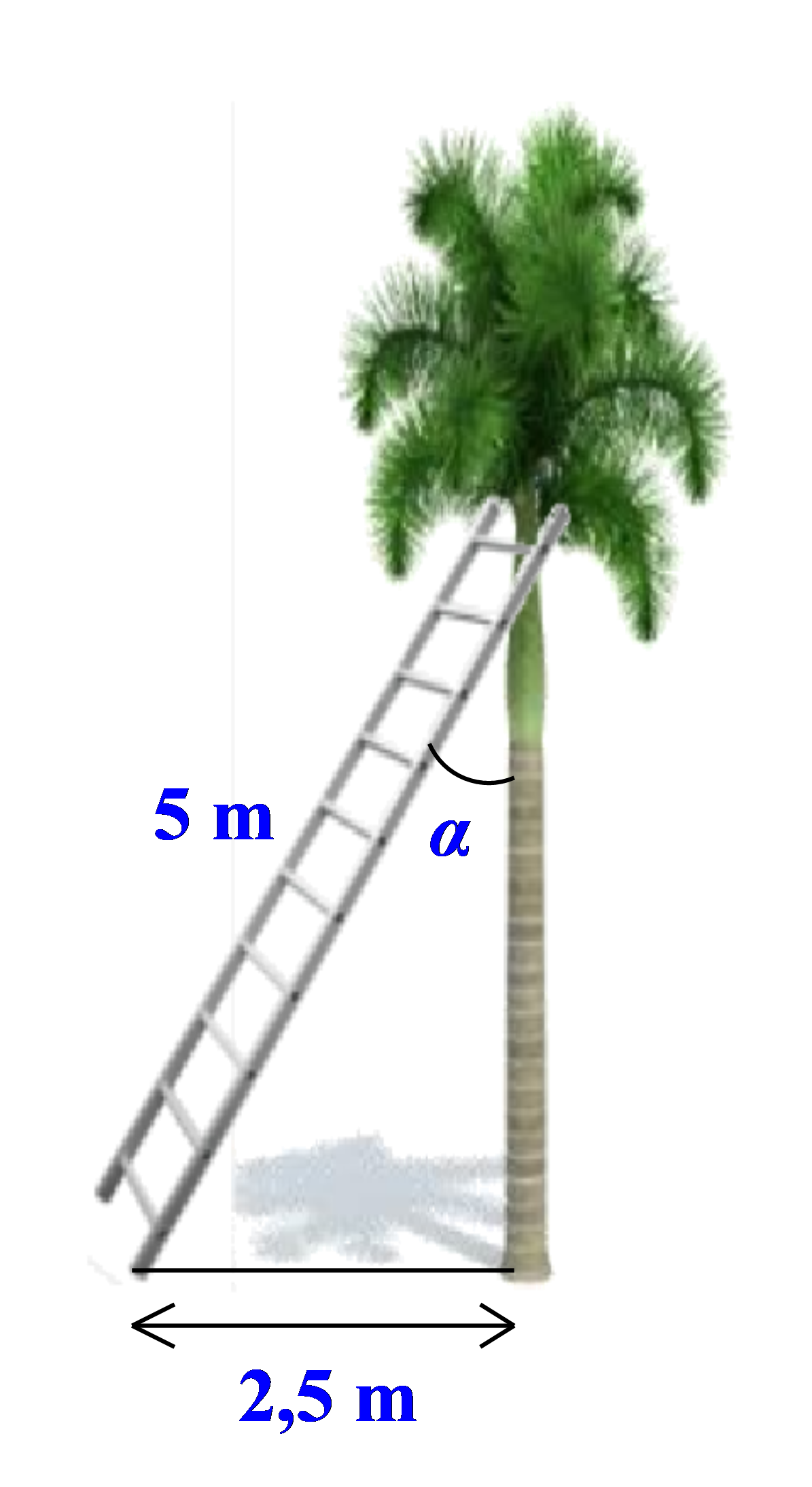
A. \[\alpha = 60^\circ \].
B. \[\alpha = 45^\circ \].
C. \[\alpha = 40^\circ \].
D. \[\alpha = 30^\circ \].
Tia nắng chiếu qua điểm \[B\] của tòa nhà tạo với mặt đất một góc \[x\] và tạo với cạnh \[AB\] của tòa nhà một góc \[y\] (hình vẽ). Cho biết \[{\rm{cos}}x \approx 0,78\] và \[\cot x \approx 1,25\]. Tính \[\sin y\] và \[\tan y\] (kết quả làm tròn đến hàng phần trăm).
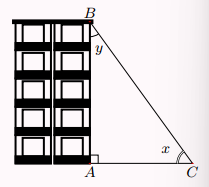
A. Sin y \( \approx \)0,75; tan y \( \approx \) 1,45
B. Sin y \( \approx \)0,78; tan y \( \approx \) 1,25
C. Sin y \( \approx \)0,35; tan y \( \approx \) 1,35
D. Sin y \( \approx \)0,45; tan y \( \approx \) 1,15
Tính chiều cao của tháp canh trong hình bên (kết quả làm tròn đến hàng phần trăm).
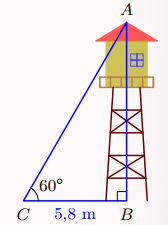
A. \(10,05\left( m \right)\)
B. \(10,04\left( m \right)\)
C. \(10,045\left( m \right)\)
D. \(10,03\left( m \right)\)
Hình bên mô tả một chiếc thang có chiều dài \[AB = 4\]m được đặt dựa vào tường, khoảng cách từ chân thang đến chân tường là \[BH = 1,5\]m. Tính góc tạo bởi cạnh \[AB\] và phần tường nằm ngang trên mặt đất (làm tròn kết quả đến hàng đơn vị)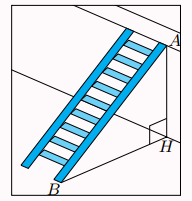
A. \({67^0}\)
B. \({69^0}\)
C. \({66^0}\)
D. \({68^0}\)
Tam giác \(ABC\)ở hình bên (có \(\widehat A = 90^\circ \)) mô tả cột cờ \(AB\) và bóng nắng của cột cờ trên mặt đất là \(AC\). Người ta đo được độ dài \(AC = 12m\) và \(\widehat C = 40^\circ \). Tính chiều cao \(AB\) của cột cờ. (kết quả làm tròn đến hàng phần trăm của mét).
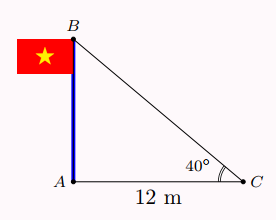
A. \(10,06\left( m \right)\)
B. \(10,069\left( m \right)\)
C. \(10,07\left( m \right)\)
D. \(10,7\left( m \right)\)
Tại một thời điểm trong ngày, các tia nắng mặt trời tạo với mặt đất một góc bằng \[{\rm{55}}^\circ \], bóng của một cây xanh trên mặt đất dài \[14,25\,\,{\rm{m}}\] (tham khảo hình vẽ). Tính chiều cao \[AH\]của cây ra đơn vị mét và làm tròn kết quả đến hai chữ số phần thập phân.

A. \[AH \approx 20,00\,\,{\rm{m}}\].
B. \[AH \approx 20,35\,\,{\rm{m}}\].
C. \[AH \approx {\rm{11,67}}\,\,{\rm{m}}\].
D. \[AH \approx 22,50\,\,{\rm{m}}\].
Một cái thang dài \[4,8\,\,{\rm{m}}\] dựa vào tường và tạo với tường một góc \[{\rm{32}}^\circ \]. Chiều cao của thang so với mặt đất là bao nhiêu mét? (làm tròn kết quả đến chữ số thập phân thứ nhất)
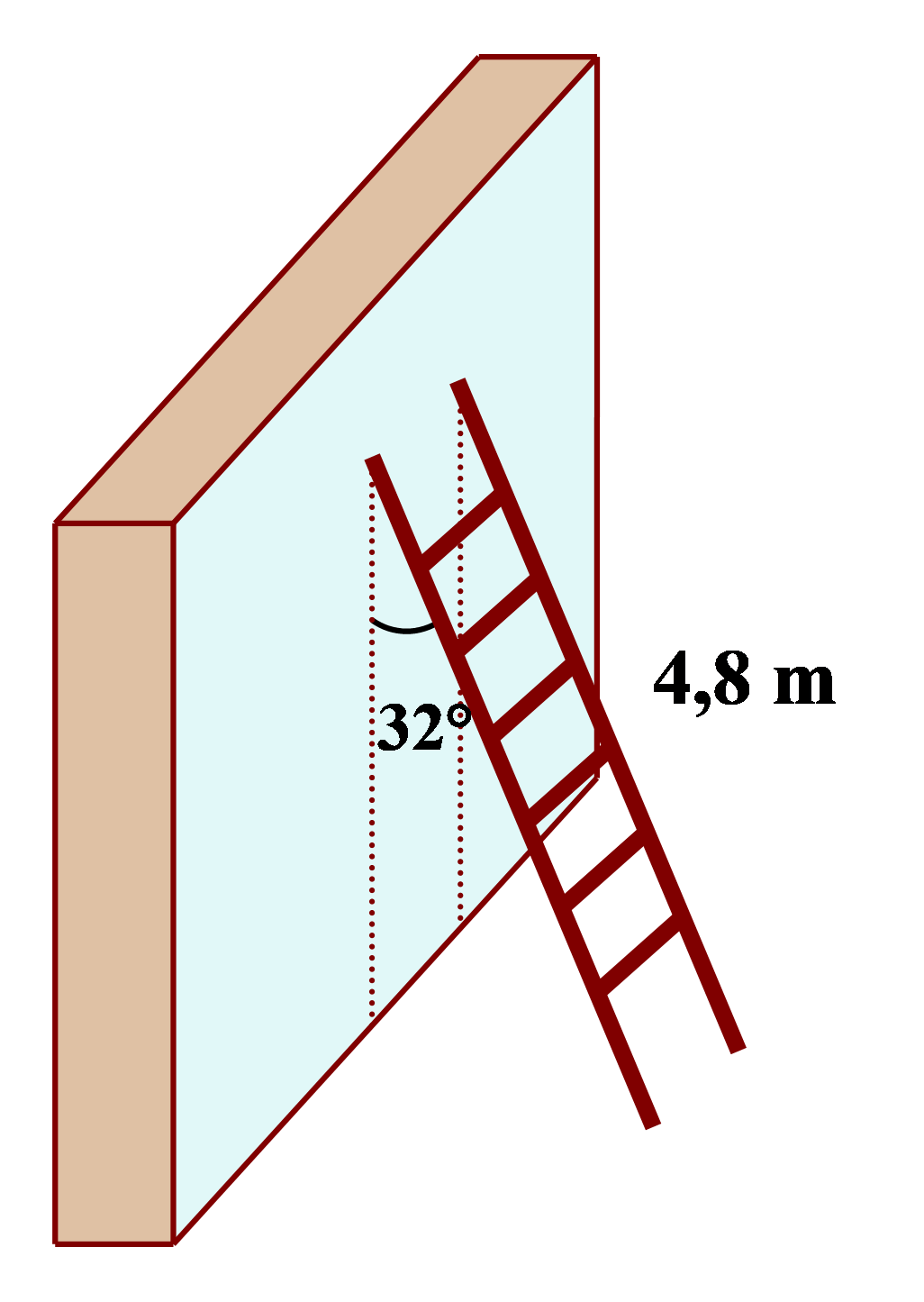
A. \[3,6\,\,{\rm{m}}\].
B. \[4,0\,\,{\rm{m}}\].
C. \[4,1\,\,{\rm{m}}\].
D. \[4,5\,\,{\rm{m}}\].
Một cầu thủ sút bóng bị va vào mép bên trên của cầu môn và bị bật ngược trở lại. Biết cầu môn cao \[2,4\,\,{\rm{m}}\]và khoảng cách từ vị trí sút bóng đến chân cầu môn là \[25\,\,{\rm{m}}\]. Tính góc \[\alpha \]tạo bởi đường đi của quả bóng và mặt đất (kết quả làm tròn đến phút).
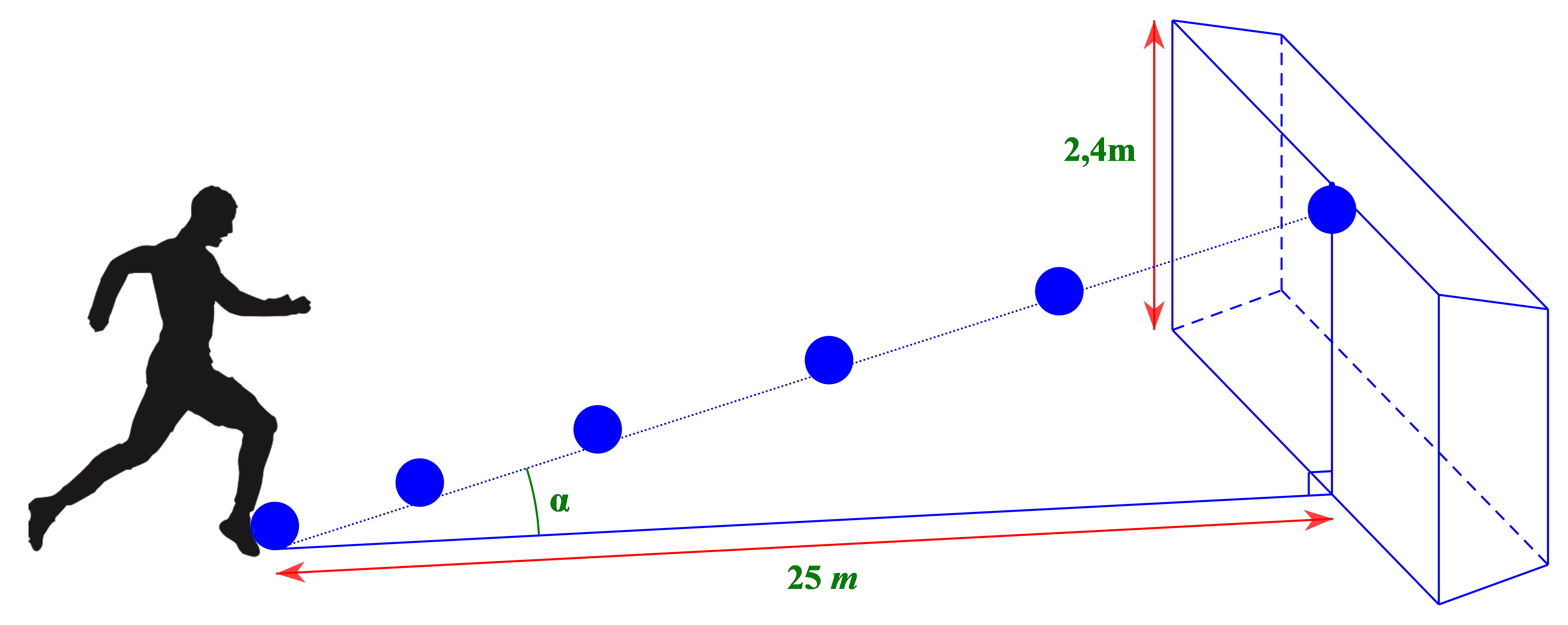
A. \[\alpha = {\rm{5}}^\circ {\rm{30'}}\].
B. \[\alpha \approx {\rm{5}}^\circ 20'\].
C. \[\alpha \approx {\rm{5}}^\circ 31'\].
D. \[\alpha \approx {\rm{5}}^\circ 29'\].
Một khúc sông rộng khoảng \[130\,\,{\rm{m}}\]. Một con đò dự định chèo từ bờ bên này sang bờ bên kia theo phương vuông góc với bờ sông, nhưng do bị dòng nước đẩy xiên nên phải chèo khoảng \[150\,\,{\rm{m}}\]mới sang được bờ bên kia. Vậy dòng nước đã đẩy con đò lệch đi một góc so với phương dự định ban đầu là bao nhiêu độ? (làm tròn kết quả đến độ)
A. \[{\rm{30}}^\circ \].
B. \[29^\circ \].
C. \[{\rm{41}}^\circ \].
D. \[6{\rm{0}}^\circ \].
Trên một cái thang dài \[3,5\,\,{\rm{m}}\] người ta ghi: “Để đảm bảo an toàn khi dùng thang, phải đặt thang này tạo với mặt đất một góc có độ lớn từ \[6{\rm{0}}^\circ \]đến \[7{\rm{0}}^\circ \]”. Gọi \[x\,\,\left( {\rm{m}} \right)\] (với \[x > 0\]) là khoảng cách từ chân thang đến chân tường để đảm bảo an toàn khi sử dụng chiếc thang này, tìm điều kiện của \[x\]. Trong các kết quả sau, kết quả nào đúng?(làm tròn kết quả đến hai chữ số phần thập phân).
A. \[1,20\, < x < 1,75\].
B. \[1,20\, \le x \le 1,75\].
C. \[x = 1,20\] hoặc \[x = 1,75\].
D. \[1,20 \le x < 1,75\].
Một máy bay cất cánh theo phương hợp với mặt đất một góc \[{\rm{23}}^\circ \]. Hỏi muốn đạt độ cao \[2\,500\,\,{\rm{m}}\], máy bay phải bay một đoạn đường \[x\] dài bao nhiêu mét?(làm tròn kết quả đến mét)
A. \[x \approx 7061\,\,{\rm{m}}\].
B. \[x \approx 6398\,\,{\rm{m}}\].
C. \[x \approx 4716\,\,{\rm{m}}\].
D. \[x \approx 5890\,\,{\rm{m}}\].
Treo quả cầu kim loại nhỏ vào giá thí nghiệm bằng sợi dây mảnh nhẹ không dãn. Khi quả cầu đứng yên tại vị trí cân bằng, dẫy treo có phương thẳng đứng. Kéo quả cầu khỏi vị trí cân bằng một đoạn nhỏ rồi buông ra thì quả cầu sẽ chuyển động qua lại quanh vị trí cân bằng. Khi kéo quả cầu khỏi vị trí cân bằng, giả sử tâm \[A\] của quả cầu cách \[B\] một khoảng \[AB = 60\]cm và cách vị trí cân bằng một khoảng \[AH = 20\]cm. Tính số đo góc \[\alpha \] tạo bởi sợi dây \[BA\] và vị trí cân bằng (làm tròn kết quả đến hàng đơn vị của độ).
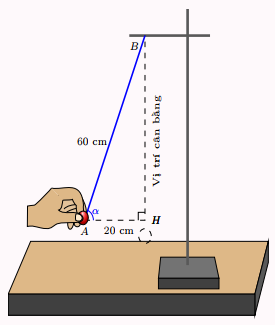
A. \({18^0}\)
B. \({19^0}\)
C. \({20^0}\)
D. \({21^0}\)
Một người đứng cách chân tháp \[13,65{\rm{ m}}\] nhìn lên đỉnh tháp với phương nhìn hợp với phương nằm ngang một góc bằng \[{\rm{58}}^\circ \]. Biết mắt của người đó cách chân của mình một khoảng \[1,55{\rm{ m}}\], hỏi tháp cao bao nhiêu mét? (làm tròn đến chữ số thập phân thứ hai)

A. \[23,38\,\,{\rm{m}}\].
B. \[21,84\,\,{\rm{m}}\].
C. \[23,39\,\,{\rm{m}}\].
D. \[21,85\,\,{\rm{m}}\].
Một con thuyền đi với vận tốc \[2\,\,{\rm{km/h}}\] từ bờ bên này sang bờ bên kia hết \[36\] phút. Do nước chảy mạnh nên đường đi của con thuyền tạo với bờ một góc \[{\rm{80}}^\circ \](tham khảo hình vẽ). Nếu coi khúc sông đó có hai bờ song song thì chiều rộng của khúc sông đó là bao nhiêu mét ? (làm tròn kết quả đến chữ số thập phân thứ nhất).

A. \[1218,5\,\,{\rm{m}}\].
B. \[1181,8\,\,{\rm{m}}\].
C. \[208,4\,\,{\rm{m}}\].
D. \[6910,5\,\,{\rm{m}}\].
Hai bạn Việt và Nam cùng chơi thả diều trên một bãi đất phẳng, sợi dây diều của bạn Việt có độ dài \[100\,\,{\rm{m}}\] và dây diều tạovới phương ngang một góc \[{\rm{42}}^\circ \] còn sợi dây diều của bạn Nam có độ dài \[96\,\,{\rm{m}}\] và dây diều tạovới phương ngang một góc \[{\rm{45}}^\circ \]. Cho biết tầm mắt của cả hai bạn đều là \[1,55\,\,{\rm{m}}\] và coi các dây diều được thả hết và căng thẳng (tham khảo hình vẽ). Trong các kết luận sau, kết luận nào đúng? (làm tròn kết quả đến chữ số thập phân thứ hai).

A. So với mặt đất thì diều của bạn Việt lên cao hơn diều của bạn Nam và cao hơn \[0,25\,\,{\rm{m}}\].
B. So với mặt đất thì diều của bạn Nam lên cao hơn diều của bạn Việt và cao hơn \[0,97\,\,{\rm{m}}\].
C. So với mặt đất thì diều của bạn Nam lên cao hơn diều của bạn Việt và cao hơn \[1,03\,\,{\rm{m}}\].
D. So với mặt đất thì diều của hai bạn Việt và Nam lên cao bằng nhau.
Để phục vụ việc di chuyển của khách hàng giữa các tầng hàng trong siêu thị, người chủ đầu tư thường cho lắp hệ thống thang cuốn tự động. Biết rằng thang cuốn có góc nghiêng là \[35^\circ \]so với phương ngang và tốc độ truyền là \[0,65\,\,{\rm{m/s}}\], khoảng cách giữa hai tầng liên tiếp là \[4,2\,\,{\rm{m}}\]. Hỏi một người khi bước vào thang cuốn và đứng yên thì cần bao nhiêu giây để có thể di chuyển từ tầng \[1\] lên tầng \[2\]? (làm tròn kết quả đến chữ số thập phân thứ nhất)
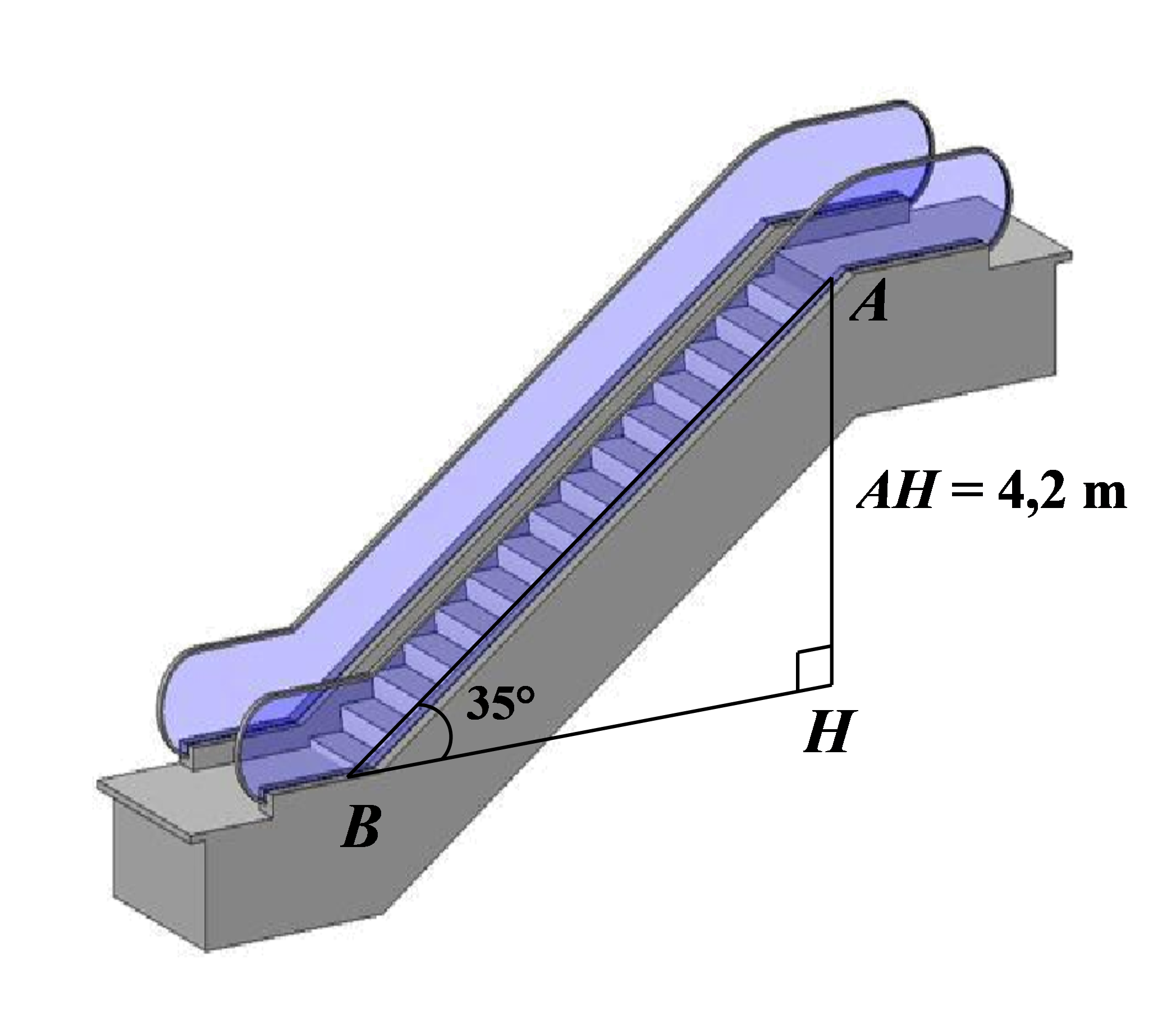
A. \[11,3\] giây.
B. \[11,2\] giây.
C. \[7,9\] giây.
D. \[7,8\] giây.
Một người đang ở trên tầng thượng của một tòa nhà quan sát con đường chạy thẳng đến chân tòa nhà. Anh ta nhìn thấy một người điều khiển chiếc xe máy đi về phía tòa nhà với phương nhìn tạo với phương nằm ngang một góc bằng\[30^\circ \]. Sau \[6\] phút, người quan sát vẫn nhìn thấy người điều khiển chiếc xe máy với phương nhìn tạo với phương nằm ngang một góc bằng\[60^\circ \]. Hỏi sau bao nhiêu phút nữa thì xe máy sẽ chạy đến chân tòa nhà? Cho biết vận tốc xe máy không đổi.

A. \[5\] phút.
B. \[4,5\] phút.
C. \[3,5\] phút.
D. \[3\] phút.
Để xác định chiều cao \[AH\] của một ngọn núi, người quan sát đứng từ hai vị trí \[B\]và \[C\] cách nhau \[475\,\,{\rm{m}}\] trên Mặt đất. Tại vị trí \[B\], người đó quan sát đỉnh núi với phương nhìn tạo với phương nằm ngang một góc bằng\[34^\circ \]; tại vị trí \[C\], người đó quan sát đỉnh núi với phương nhìn tạo với phương nằm ngang một góc bằng\[30^\circ \] (như hình vẽ dưới đây). Tính chiều cao của ngọn núi (đơn vị mét), biết rằng tầm mắt của người quan sát là \[{\rm{1,6}}\,\,{\rm{m}}\] và giả thiết ba điểm \[H\], \[B\], \[C\] thẳng hàng (kết quả làm tròn đến số thập phân thứ nhất).
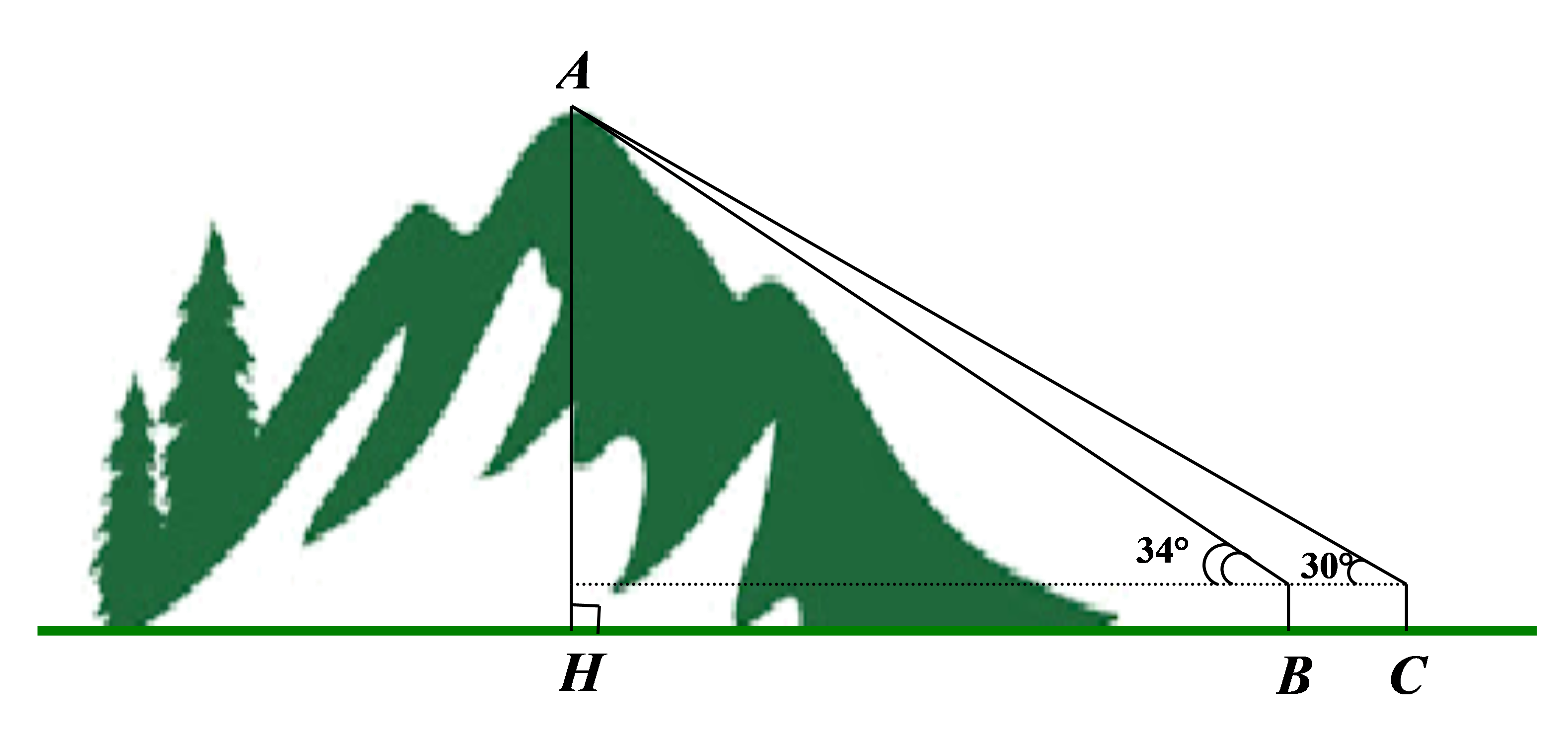
A. \[1845,5{\rm{ m}}\].
B. \[2153,8{\rm{ m}}\].
C. \[1905,5\,\,{\rm{m}}\].
D. \[219,6{\rm{ m}}\].
Để xác định khoảng cách từ một gốc cây \[A\] trên một hòn đảo nhỏ giữa biển đến vị trí con sao biển \[C\] trên bãi cát (như hình bên dưới), người ta chọn một điểm \[B\] trên bãi biển cách điểm \[C\] một khoảng \[1225\,\,{\rm{m}}\] và dùng giác kế ngắm xác định được \[\widehat {ABC} = {75^{\rm{o}}}\]; \[\widehat {ACB} = {65^{\rm{o}}}\]. Tính khoảng cách \[AC\](kết quả làm tròn đến đơn vị mét).
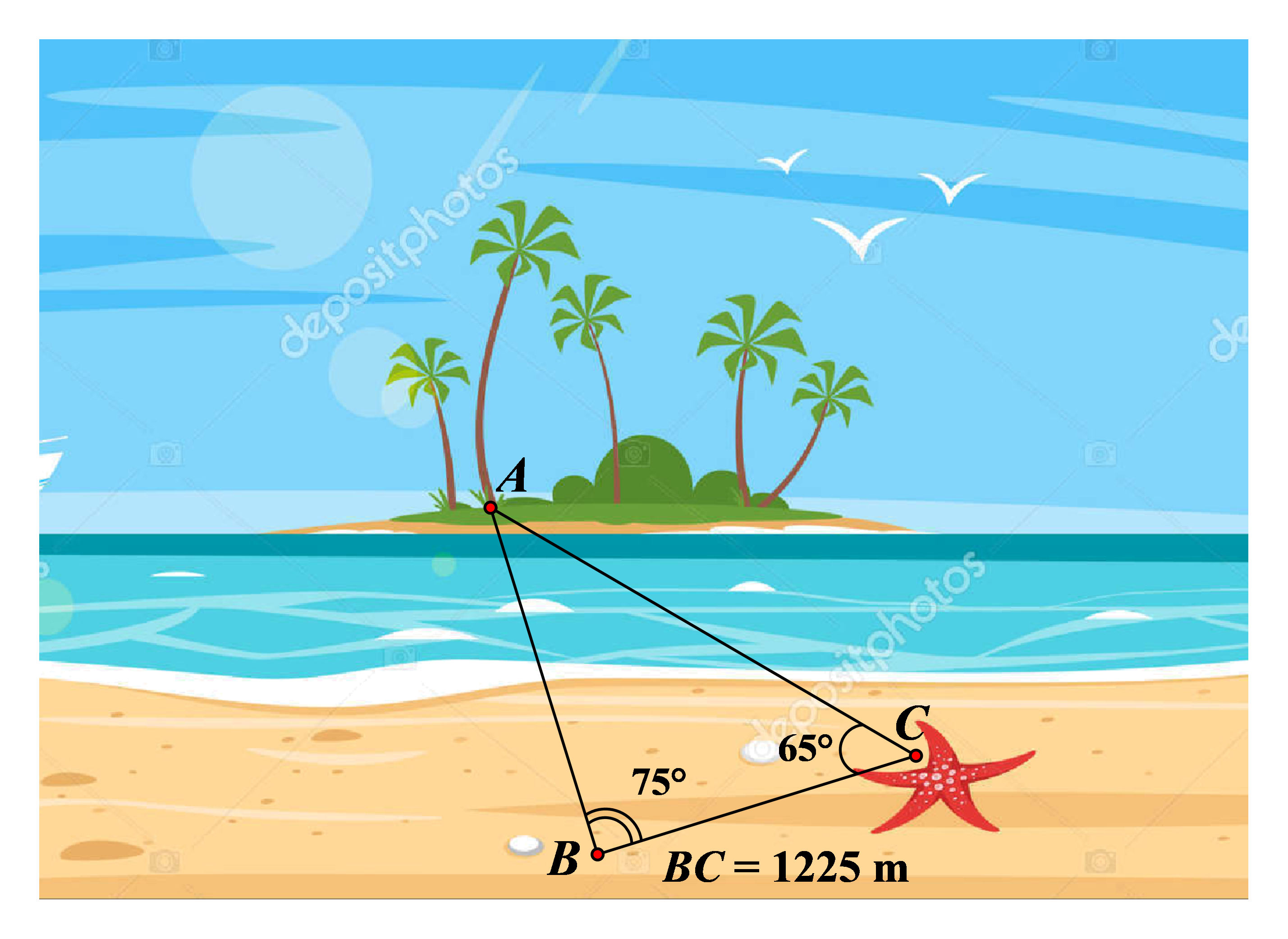
A. \[1841{\rm{ m}}\].
B. \[1783{\rm{ m}}\].
C. \[1652\,\,{\rm{m}}\].
D. \[1906{\rm{ m}}\].

