6 CÂU HỎI
Cho hình chóp S.ABCD, đáy ABCD là hình vuông, . Gọi là mặt phẳng chứa AB và vuông góc với (SCD), cắt chóp S.ABCD theo thiết diện là hình gì?
A. hình bình hành.
B. hình thang vuông.
C. hình thang không vuông.
D. hình chữ nhật.
Cho hình chóp S.ABCD với ABCD là hình chữ nhật tâm O có AB = a, AD = 2a. SA vuông góc với đáy và SA = a. Gọi (P) là mặt phẳng qua SO và vuông góc với (SAD). Diện tích thiết diện của (P) và hình chóp S.ABCD bằng bao nhiêu?
A.
B.
C.
D.
Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến . Lấy A, B cùng thuộc và lấy C trên (P), D trên (Q) sao cho 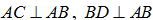 và AB = AC = BD = a. Diện tích thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng đi qua A và vuông góc với CD là?
và AB = AC = BD = a. Diện tích thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng đi qua A và vuông góc với CD là?
A. 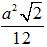
B. 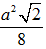
C. 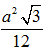
D. 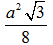
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, với AB = c, AC = b, cạnh bên AA' = h. Mặt phẳng (P) đi qua A' và vuông góc với B'C. Thiết diện của lăng trụ cắt bởi mặt phẳng (P) có hình:
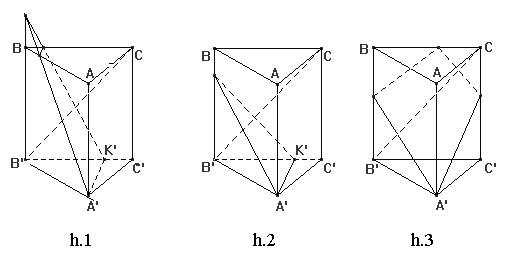
A. h.1 và h.2
B. h.2 và h.3
C. h.2
D. h.1
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Cắt hình lập phương bởi mặt phẳng trung trực của AC'. Thiết diện là hình gì?
A. Hình vuông.
B. Lục giác đều.
C. Ngũ giác đều.
D. Tam giác đều.
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Cắt hình lập phương bởi mặt phẳng trung trực của AC'. Diện tích thiết diện là
A. 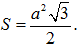
B. 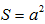
C. 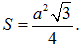
D.