12 CÂU HỎI
Cho hình vuông ABCD, M là điểm nằm trên đoạn thẳng AC sao cho \(AM = \frac{{AC}}{4},\) N là trung điểm của đoạn thẳng DC. Tìm mệnh đề đúng?
A. Tam giác BMN là tam giác vuông;
B. Tam giác BMN là tam giác cân;
C. Tam giác BMN là tam giác đều;
D. Tam giác BMN là tam giác vuông cân.
Tổng tất cả các giá trị thực của tham số m để hàm số y = 3x3 + 2(m + 1)x2 – 3mx + m – 5 có hai điểm cực trị x1, x2 đồng thời y(x1).y(x2) = 0 là
A. −8;
B. \(3\sqrt {11} - 13\);
C. −39;
D. −21.
Bạn Sơn tạo các hình bằng những chiếc tăm giống nhau theo sơ đồ nhứ hình trên (Hình thứ n có n2 ô vuông giống nhau và mỗi cạnh hình vuông là một chiếc tăm). Hỏi Sơn phải thêm bao nhiêu chiếc tăm vào hình thứ 2018 để được hình thứ 2019.
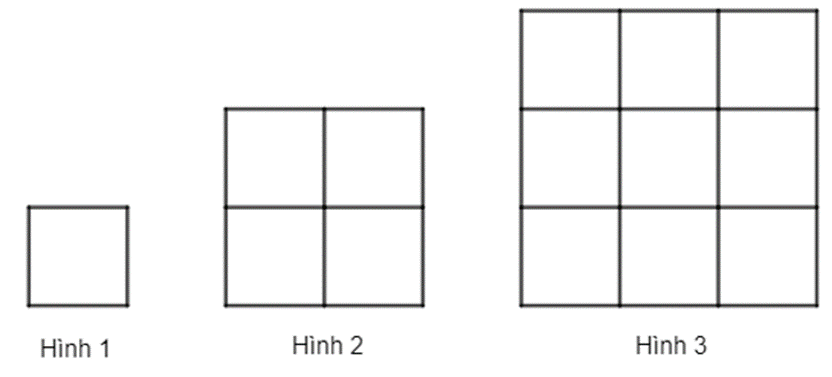
A. 8076;
B. 7698;
C. 5346;
D. 6782.
Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của (SAB) và (SCD) là:
A. Đường thẳng qua Svà song song với AD;
B. Đường thẳng quaSvà song song với CD;
C. Đường SO với O là tâm hình bình hành;
D. Đường thẳng qua S và cắt AB.
Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của mp(SAD) và mp(SBC) là đường thẳng song song với đường thẳng nào trong số các đường thẳng sau?
A. AC;
B. BD;
C.AD;
D. SC.
Tính đạo hàm số \(y = n\left( {x + \sqrt {{x^2} + 1} } \right)\)
A. \(y' = \frac{1}{{\sqrt {{x^2} + 1} }}\);
B. \(y' = \frac{1}{{x + \sqrt {{x^2} + 1} }}\);
C. \(y' = \frac{{2x}}{{x + \sqrt {{x^2} + 1} }}\);
D. \(y' = \frac{1}{{2\sqrt {{x^2} + 1} }}\).
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn số phức z thỏa mãn z(1 + i) là số thực là:
A. Đường trong bán kính bằng 1;
B. Trục Ox;
C. Đường thẳng y = −x;
D. Đường thẳng y = x.
Trong mặt phẳng phức, tập hợp các điểm biểu diễn các số phức z thỏa mãn \(z.\overline z = 1\) là
A. Một đường thẳng;
B. Một đường tròn;
C. Một elip;
D. Một điểm.
Cho hình chóp S.ABCD, đáy là hình bình hành tâm O. Gọi M, N, P, Q lần lượt là trung điểm SA, SB, SC và SD. Tìm giao tuyến của (MNPQ) và (SAC).
A. MN;
B. QM;
C. SO;
D.MP.
Xác định hàm số bậc hai y = ax2 + bx + c biết đồ thị của nó có đỉnh I(1; −1) và đi qua điểm A(2; 0)
A. y = x2 − 3x + 2;
B. y = 2x2 − 4x + 3;
C. y = x2 − 2x;
D. y = x2 + 2x.
Xác định hàm số bậc hai y = 2x2 + bx + c biết đồ thị của nó có đỉnh I(−1; −2).
A. y = 2x2 – 4x + 4;
B. y = 2x2 – 4x;
C. y = 2x2 – 3x + 4;
D. y = 2x2 + 4x.
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác vẽ các hình vuông ABDE, ACFG và BCHI. Ta có:
A. SACFG = SBCHI + SABDE;
B. SBCHI = SABDE + SACFG;
C. SABDE = SBCHI + SACFG;
D. SBCHI = SACFG − SABDE.
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
