5 CÂU HỎI
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(– 4;1); B(2; 4); C(2; –2). Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác đã cho.
A. \(I\left( {\frac{1}{4};1} \right)\);
B. \(I\left( {\frac{{ - 1}}{4};1} \right)\);
C. \(I\left( {1;\frac{1}{4}} \right)\);
D. \(I\left( {1;\frac{{ - 1}}{4}} \right)\).
Hệ bất phương trình \(\left\{ \begin{array}{l}2{\rm{x}} + m < 0{\rm{ (1)}}\\3{{\rm{x}}^2} - x - 4 \le 0{\rm{ (2)}}\end{array} \right.\) vô nghiệm khi và chỉ khi:
A. \(m > \frac{{ - 8}}{3}\);
B. m < 2;
C. m ≥ 2;
D. \(m \ge \frac{{ - 8}}{3}\).
Cho hàm số đa thức y = f(x) có đạo hàm trên ℝ, f(0) < 0 và đồ thị hình bên dưới là đồ thị của đạo hàm f’(x). Hỏi hàm số g(x) = |f(x) + 3x| có bao nhiêu điểm cực trị?
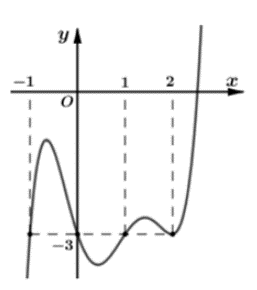
A. 4;
B. 5;
C. 3;
D. 6.
Cho tam giác ABC. Gọi I là điểm thỏa mãn \(\overrightarrow {IA} + 2\overrightarrow {IB} + 3\overrightarrow {IC} = \overrightarrow 0 \). Khi đó:
A. \(\overrightarrow {AI} = \frac{1}{3}\overrightarrow {AB} - \frac{1}{2}\overrightarrow {AC} \);
B. \(\overrightarrow {AI} = - \frac{1}{3}\overrightarrow {AB} - \frac{1}{2}\overrightarrow {AC} \);
C. \(\overrightarrow {AI} = \frac{1}{3}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \);
D. \(\overrightarrow {AI} = - \frac{1}{3}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \).
Hình dưới đây có bao nhiêu hình tam giác, bao nhiêu hình tứ giác?
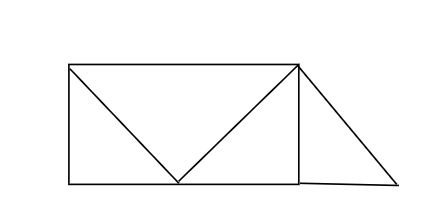
A. 4 hình tam giác, 5 hình tứ giác;
B. 4 hình tam giác, 4 hình tứ giác;
C. 5 hình tam giác, 4 hình tứ giác;
D. 5 hình tam giác, 5 hình tứ giác.
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải