10 CÂU HỎI
Cho tam giác ABC. Gọi M là điểm được xác định: \(4\overrightarrow {BM} - 3\overrightarrow {BC} = \overrightarrow 0 \). Khi đó vectơ \(\overrightarrow {AM} \) bằng:
A. \(\overrightarrow {AB} + \overrightarrow {AC} \)
B. \(\frac{1}{2}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \)
C. \(\frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} \)
D. \(\frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} \)
Cho biết log25 7 = a và log2 5 = b. Tính \({\log _{\sqrt[3]{5}}}\frac{{49}}{8}\) theo a, b.
A. \(\frac{{2(ba - 3)}}{b}\);
B. \(\frac{{ - 4ba + 3}}{b}\);
C. \(\frac{b}{{4{\rm{a}}b + 1}}\);
D. \(\frac{{3(4{\rm{a}}b - 3)}}{b}\).
Diện tích miếng bìa có kích thước theo hình vẽ bên là:
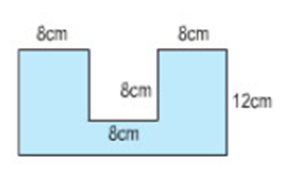
A. 96 cm2;
B. 192 cm2;
C. 224 cm2;
D. 288 cm2.
Chu kì của hàm số y = 3 + 2sin2 2x là
A.\(\frac{\pi }{2}\);
B. \(\frac{\pi }{4}\);
C. π;
D. 2 π.
Cho hình lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng a, đường thẳng BC’ tạo với mặt phẳng (ACC’A’) một góc 30°. Tính thể tích V của khối lăng trụ ABC.A’B’C’.
A. \(V = \frac{{\sqrt 6 }}{4}{a^3}\);
B. \(V = \frac{{{a^3}}}{8}\);
C. \(V = \frac{{\sqrt 3 }}{4}{a^3}\);
D. \(V = \frac{3}{8}{a^3}\).
Cho một hình chóp tam giác đều có cạnh bên bằng b và cạnh bên tạo với mặt phẳng đáy một góc α. Thể tích của hình chóp là:
A. \(\frac{3}{4}{b^3}{\rm{co}}{{\rm{s}}^2}\alpha \sin \alpha \);
B. \(\frac{{\sqrt 3 }}{4}{b^3}{\rm{co}}{{\rm{s}}^2}\alpha \sin \alpha \);
C. \(\frac{3}{4}{b^3}{\rm{cos}}\alpha {\sin ^2}\alpha \);
D. \(\frac{{\sqrt 3 }}{4}{b^3}{\rm{cos}}\alpha \sin \alpha \).
Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và đáy bằng 30°. Thể tích khối chóp S.ABC bằng:
A. \(\frac{{{a^3}\sqrt 2 }}{{18}}\);
B. \(\frac{{{a^3}\sqrt 2 }}{{36}}\);
C. \(\frac{{{a^3}\sqrt 3 }}{{18}}\);
D. \(\frac{{{a^3}\sqrt 3 }}{{36}}\).
Cho hình lăng trụ ABC.A’B’C biết A’.ABC là tứ diện đều cạnh bằng a. Tính thể tích khối A’BCC’B’.
A. \(V = \frac{{{a^3}}}{2}\);
B. \(V = \frac{{\sqrt 2 {a^3}}}{6}\);
C. \(V = \frac{{\sqrt 2 {a^3}}}{{12}}\);
D. \(V = \frac{{\sqrt 3 {a^3}}}{3}\).
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân với AB = AC = a, \(\widehat {BAC} = 120^\circ \). Mặt phẳng (AB’C’) tạo với đáy một góc 60°. Tính thể tích V của khối lăng trụ đã cho
A. \(\frac{{3{{\rm{a}}^3}}}{8}\);
B. \(\frac{{{\rm{9}}{{\rm{a}}^3}}}{8}\);
C. \(\frac{{{{\rm{a}}^3}}}{8}\);
D. \(\frac{{{\rm{3}}{{\rm{a}}^3}}}{4}\).
Tìm tất cá các giá trị thực của tham số m để hàm số \(y = \frac{1}{3}{x^3} - 2m{{\rm{x}}^2} + 4{\rm{x}} - 5\)
đồng biến trên ℝ.
A. 0 < m < 1;
B. – 1 ≤ m ≤ 1;
C. 0 ≤ m ≤ 1;
D. – 1 < m < 1.
Gợi ý cho bạn
Trắc nghiệm củng cố
10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải