Quiz

58 câu Chuyên đề Toán 12 Bài 1: Lũy thừa - Hàm số lũy thừa có đáp án

VietJackToánLớp 126 lượt thi

Bắt đầu ngay

58 câu hỏi

Hiển thị đáp án

1. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho x là số thực dương. Biểu thức $\sqrt[4]{x^{2} \sqrt[3]{x}}$ được viết dưới dạng lũy thừa với số mũ hữu tỉ là

$x^{\frac{7}{12}} .$

$x^{\frac{5}{6}} .$

$x^{\frac{12}{7}} .$

$x^{\frac{6}{5}} .$

Xem đáp án

2. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hai số thực dương a và b. Biểu thức $\sqrt[5]{\frac{a}{b} \sqrt[3]{\frac{b}{a} \sqrt{\frac{a}{b}}}}$ được viết dưới dạng lũy thừa với số mũ hữu tỉ là

${(\frac{a}{b})}^{\frac{7}{30}} .$

${(\frac{a}{b})}^{\frac{31}{30}} .$

${(\frac{a}{b})}^{\frac{30}{31}} .$

${(\frac{a}{b})}^{\frac{1}{6}} .$

Xem đáp án

3. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho $P = {(x^{\frac{1}{2}} - y^{\frac{1}{2}})}^{2} {(1 - 2 \sqrt{\frac{y}{x}} + \frac{y}{x})}^{- 1}$ . Biểu thức rút gọn của P là

x + 1

x - 1

Xem đáp án

4. Trắc nghiệm

• 1 điểm • Không giới hạn

Rút gọn biểu thức $(\frac{a^{0,5} + 2}{a + 2 a^{0,5} + 1} - \frac{a^{0,5} - 2}{a - 1}) . \frac{a^{0,5} + 1}{a^{0,5}}$ (với $0 < a \neq 1$ ) ta được

$\frac{a - 2}{2} .$

$\frac{a - 1}{2} .$

$\frac{2}{1 - a} .$

$\frac{2}{a - 1} .$

Xem đáp án

5. Trắc nghiệm

• 1 điểm • Không giới hạn

Rút gọn biểu thức ${[\frac{x \sqrt{x} - x}{(\frac{\sqrt[4]{x^{3}} - 1}{\sqrt[4]{x} - 1} - \sqrt{x}) (\frac{\sqrt[4]{x^{3}} + 1}{\sqrt[4]{x} + 1} - \sqrt{x})}]}^{3}$ (với $x > 0, x \neq 1$ ) ta được

$x^{2} .$

$- x^{2} .$

$- x^{3} .$

$x^{3} .$

Xem đáp án

6. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho $f (x) = \frac{2018^{x}}{2018^{x} + \sqrt{2018}} .$ Tính giá trị biểu thức sau đây ta được $S = f (\frac{1}{2019}) + f (\frac{2}{2019}) + ... + f (\frac{2018}{2019})$

S = 2018

S = 2019

S = 1009

$S = \sqrt{2018} .$

Xem đáp án

7. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho $9^{x} + 9^{- x} = 23.$ Tính giá trị của biểu thức $P = \frac{5 + 3^{x} + 3^{- x}}{1 - 3^{x} - 3^{- x}}$ ta được

-2

$\frac{3}{2} .$

$\frac{1}{2} .$

$\frac{- 5}{2} .$

Xem đáp án

8. Trắc nghiệm

• 1 điểm • Không giới hạn

Khẳng định nào sau đây đúng?

$a^{- n}$ xác định với mọi $\forall a \in ℝ \ \{0\}; \forall n \in ℕ .$

$a^{\frac{m}{n}} = \sqrt[n]{a^{m}}; \forall a \in ℝ .$

$a^{0} = 1; \forall a \in ℝ .$

$\sqrt[n]{a^{m}} = a^{\frac{m}{n}}; \forall a \in ℝ; \forall m, n \in ℤ .$

Xem đáp án

9. Trắc nghiệm

• 1 điểm • Không giới hạn

Rút gọn biểu thức $\frac{a^{2 \sqrt{2}} - b^{2 \sqrt{3}}}{{(a^{\sqrt{2}} - b^{\sqrt{3}})}^{2}} + 1$ (với $a > 0, b > 0$ và $a^{\sqrt{2}} \neq b^{\sqrt{3}}$ ) được kết quả

$2 a^{\sqrt{2}} .$

$\frac{a^{\sqrt{2}} + b^{\sqrt{3}}}{a^{\sqrt{2}} - b^{\sqrt{3}}} .$

$\frac{2 a^{\sqrt{2}}}{a^{\sqrt{2}} - b^{\sqrt{3}}} .$

Xem đáp án

10. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho số thực dương a. Rút gọn $P = \sqrt{a \sqrt[3]{a \sqrt[4]{a \sqrt[5]{a}}}}$ ta được

$a^{\frac{25}{13}} .$

$a^{\frac{37}{13}} .$

$a^{\frac{53}{36}} .$

$a^{\frac{43}{50}} .$

Xem đáp án

11. Trắc nghiệm

• 1 điểm • Không giới hạn

Viết biểu thức $P = a . \sqrt[3]{a^{2} . \sqrt{a}} (a > 0)$ dưới dạng lũy thừa với số mũ hữu tỉ ta được

$P = a^{\frac{5}{3}} .$

$P = a^{\frac{5}{6}} .$

$P = a^{\frac{11}{6}} .$

$P = a^{2} .$

Xem đáp án

12. Trắc nghiệm

• 1 điểm • Không giới hạn

Viết biểu thức $\sqrt[5]{\frac{b}{a} \sqrt[3]{\frac{a}{b}}}, (a, b > 0)$ về dạng lũy thừa ${(\frac{a}{b})}^{m}$ ta được m bằng

$\frac{2}{15}$

$\frac{4}{15}$

$\frac{2}{5}$

$\frac{- 2}{15}$

Xem đáp án

13. Trắc nghiệm

• 1 điểm • Không giới hạn

Rút gọn biếu thức $Q = b^{\frac{5}{3}} : \sqrt[3]{b}$ với $b > 0$ ta được

$Q = b^{2} .$

$Q = b^{\frac{5}{9}} .$

$Q = b^{\frac{- 4}{3}} .$

$Q = b^{\frac{4}{3}} .$

Xem đáp án

14. Trắc nghiệm

• 1 điểm • Không giới hạn

Giả sử a là số thực dương, khác 1 và $\sqrt{a \sqrt[3]{a}}$ được viết dưới dạng $a^{α} .$ . Giá trị của $α$ là

$α = \frac{11}{6} .$

$α = \frac{5}{3} .$

$α = \frac{2}{3} .$

$α = \frac{1}{6} .$

Xem đáp án

15. Trắc nghiệm

• 1 điểm • Không giới hạn

Rút gọn biểu thức $P = x^{\frac{1}{3}} . \sqrt[6]{x}$ với $x > 0$ ta được

$P = x^{2} .$

$P = \sqrt{x} .$

$P = x^{\frac{1}{8}} .$

$P = x^{\frac{2}{9}} .$

Xem đáp án

16. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho a, b là các số thực dương. Viết biểu thức $\sqrt[12]{a^{3} b^{3}}$ dưới dạng lũy thừa với số mũ hữu tỉ ta được

$a^{\frac{3}{4}} b^{\frac{1}{2}} .$

$a^{\frac{1}{4}} b^{\frac{1}{9}} .$

$a^{\frac{1}{4}} b^{\frac{1}{4}} .$

$a^{\frac{1}{4}} b^{\frac{3}{4}} .$

Xem đáp án

17. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho a là một số dương, viết $a^{\frac{2}{3}} \sqrt{a}$ dưới dạng lũy thừa với số mũ hữu tỉ ta được

$a^{\frac{7}{6}} .$

$a^{3} .$

$a^{\frac{1}{6}} .$

$a^{2} .$

Xem đáp án

18. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho $a > 0.$ Đẳng thức nào sau đây đúng?

$\sqrt{a} \sqrt[3]{a} = \sqrt[4]{a} .$

$\frac{\sqrt{a^{3}}}{\sqrt[3]{a^{2}}} = a^{\frac{5}{6}} .$

${(a^{2})}^{4} = a^{6} .$

$\sqrt[7]{a^{5}} = a^{\frac{7}{5}} .$

Xem đáp án

19. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho biểu thức $P = \frac{{(a^{\sqrt{3} - 1})}^{\sqrt{3} + 1}}{a^{\sqrt{5} - 3} . a^{4 - \sqrt{5}}},$ với $a > 0.$ Mệnh đề nào dưới đây đúng?

$P = a^{\frac{1}{2}} .$

P = a

$P = a^{\frac{3}{2}} .$

$P = a^{\sqrt{3}} .$

Xem đáp án

20. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $f (a) = \frac{a^{\frac{2}{3}} (\sqrt[3]{a^{- 2}} - \sqrt[3]{a})}{a^{\frac{1}{8}} (\sqrt[8]{a^{3}} - \sqrt[8]{a^{- 1}})}$ với $a > 0, a \neq 1.$ Giá trị của $M = f (2017^{2018})$ là

$M = 2017^{2018} + 1.$

$M = 2017^{1009} .$

$M = 2017^{1009} + 1.$

$M = - 2017^{1009} - 1.$

Xem đáp án

21. Trắc nghiệm

• 1 điểm • Không giới hạn

Giá trị của biểu thức $P = {(7 + 4 \sqrt{3})}^{2017} {(7 - 4 \sqrt{3})}^{2016}$ bằng

$7 - 4 \sqrt{3} .$

$7 + 4 \sqrt{3} .$

${(7 + 4 \sqrt{3})}^{2016} .$

Xem đáp án

22. Trắc nghiệm

• 1 điểm • Không giới hạn

Giá trị của biểu thức $P = {(9 + 4 \sqrt{5})}^{2017} {(9 - 4 \sqrt{5})}^{2016}$ bằng

$9 - 4 \sqrt{5} .$

$9 + 4 \sqrt{5} .$

${(9 - 4 \sqrt{5} .)}^{2017} .$

Xem đáp án

23. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho $4^{x} + 4^{- x} = 14.$ Giá trị của biểu thức $P = \frac{10 - 2^{x} - 2^{- x}}{3 + 2^{x} + 2^{- x}}$ là

P = 2

$P = \frac{1}{2} .$

$P = \frac{6}{7} .$

P = 7

Xem đáp án

24. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho $25^{x} + 25^{- x} = 7.$ Giá trị của biểu thức $P = \frac{4 - 5^{x} - 5^{- x}}{9 + 5^{x} + 5^{- x}}$ là

P = 12

$P = 12^{- 1} .$

$P = \frac{1}{9} .$

P = 2

Xem đáp án

25. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $f (x) = \frac{9^{x}}{9^{x} + 3}; x \in ℝ$ và a, b thỏa a + b = 1. Giá trị f(a) + f(b) bằng

-1.

$\frac{1}{2}$

Xem đáp án

26. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $f (x) = \frac{4^{x}}{4^{x} + 2} .$ Tổng $P = f (\frac{1}{100}) + f (\frac{2}{100}) + ... + f (\frac{98}{100}) + f (\frac{99}{100})$ bằng

$\frac{99}{2} .$

$\frac{301}{6} .$

$\frac{101}{2} .$

$\frac{149}{3}$

Xem đáp án

27. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $f (x) = \frac{4^{x}}{4^{x} + 2} .$ Giá trị của biểu thức sau đây bằng

$S = f (\frac{1}{2015}) + f (\frac{2}{2015}) + f (\frac{3}{2015}) + ... + f (\frac{2013}{2015}) + f (\frac{2014}{2015})$

2014.

2015.

1008.

1007.

Xem đáp án

28. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định của hàm số $y = {(x^{2} - 6 x + 5)}^{- 3}$ là

$ℝ \ \{1; 5\} .$

(1;5)

$(- \infty; 1) \cup (5; + \infty) .$

Xem đáp án

29. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định của hảm số $y = {(- x^{2} + 5 x - 6)}^{- \frac{1}{5}}$ là

$ℝ \ \{2; 3\} .$

$(- \infty; 2) \cup (3; + \infty) .$

(2;3).

$(3; + \infty) .$

Xem đáp án

30. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định của hảm số $y = x^{\sin (2018 π)}$ là

$(0; + \infty) .$

$ℝ \ \{0\} .$

$[0; + \infty) .$

Xem đáp án

31. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định của hảm số $y = {(1 + \sqrt{x})}^{- 2019}$ là

$(0; + \infty) .$

$ℝ \ \{0\} .$

$[0; + \infty) .$

Xem đáp án

32. Trắc nghiệm

• 1 điểm • Không giới hạn

Có bao nhiêu giá trị nguyên của $m \in (- 2018; 2018)$ để hàm số $y = {(x^{2} - 2 x - m + 1)}^{\sqrt{5}}$ có tập xác định là R

4036.

2018.

2017.

Vô số

Xem đáp án

33. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm đạo hàm của hàm số $y = {(1 - x^{2})}^{- \frac{1}{4}} .$

$y^{'} = - \frac{1}{4} {(1 - x^{2})}^{- \frac{5}{4}} .$

$y^{'} = - \frac{5}{2} x {(1 - x^{2})}^{- \frac{5}{4}} .$

$y^{'} = \frac{5}{2} x {(1 - x^{2})}^{- \frac{5}{4}} .$

$y^{'} = \frac{1}{2} x {(1 - x^{2})}^{- \frac{5}{4}} .$

Xem đáp án

34. Trắc nghiệm

• 1 điểm • Không giới hạn

Tìm đạo hàm của hàm số $y = {(2 + 3 \cos 2 x)}^{4} .$

$y^{'} = - 24 {(2 + 3 \cos 2 x)}^{3} \sin 2 x .$

$y^{'} = - 12 {(2 + 3 \cos 2 x)}^{3} \sin 2 x .$

$y^{'} = 24 {(2 + 3 \cos 2 x)}^{3} \sin 2 x .$

$y^{'} = 12 {(2 + 3 \cos 2 x)}^{3} \sin 2 x .$

Xem đáp án

35. Trắc nghiệm

• 1 điểm • Không giới hạn

Đạo hàm của hàm số $y = {(x \sin x)}^{\frac{2}{3}}$ là

$y^{'} = \frac{2}{3} {(x \sin x)}^{- \frac{1}{3}} .$

$y^{'} = \frac{2}{3} {(x \sin x)}^{- \frac{1}{3}} . (\sin x + x \cos x) .$

$y^{'} = \frac{2}{3} . \frac{\sin x + x \cos x}{\sqrt[3]{x^{2} \sin^{2} x}} .$

$y^{'} = \frac{2}{3} {(x \sin x)}^{- \frac{1}{3}} . \cos x .$

Xem đáp án

36. Trắc nghiệm

• 1 điểm • Không giới hạn

Đạo hàm của hàm số $y = {(1 + \sqrt{x})}^{- \frac{2}{3}}$ là

$y^{'} = \frac{- 1}{(3 x + 3 \sqrt{x}) . \sqrt[3]{{(1 + \sqrt{x})}^{2}}} .$

$y^{'} = - \frac{2}{3} {(1 + \sqrt{x})}^{- \frac{5}{3}} . \frac{1}{\sqrt{x}} .$

$y^{'} = \frac{- 1}{(x + \sqrt{x}) . \sqrt[3]{{(1 + \sqrt{x})}^{2}}} .$

$y^{'} = - \frac{2}{3} {(1 + \sqrt{x})}^{- \frac{5}{3}} .$

Xem đáp án

37. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số y = f(x) có đồ thị như hình vẽ. Hỏi f(x) có thể là hàm số nào trong bốn hàm số dưới đây?

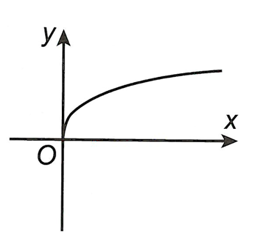
Cho hàm số y = f(x) có đồ thị như hình vẽ. Hỏi f(x) có thể là hàm số nào trong bốn hàm số dưới đây? (ảnh 1)

$f (x) = x^{\frac{1}{3}} .$

$f (x) = \sqrt[3]{x} .$

$f (x) = x^{\frac{- 1}{3}} .$

$f (x) = x^{3} .$

Xem đáp án

38. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hàm số $y = f (x) = x^{- \sqrt{2}}$ có đồ thị (C).Mệnh đề nào sau đây đúng?

Hàm số tăng trên $(0; + \infty) .$

Đồ thị (C) không có tiệm cận.

Tập xác định của hàm số là R

Hàm số không có cực trị.

Xem đáp án

39. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định D của hàm số $y = {(x^{2} - 3 x - 4)}^{\sqrt{2 - \sqrt{3}}}$ là

$D = ℝ \ \{- 1; 4\} .$

$D = (- \infty; - 1] \cup [4; + \infty) .$

$D = ℝ .$

$D = (- \infty; - 1) \cup (4; + \infty) .$

Xem đáp án

40. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hàm số sau đây, hàm số nào có tập xác định D = R?

$y = {(2 + \sqrt{x})}^{π} .$

$y = {(2 + \frac{1}{x^{2}})}^{π} .$

$y = {(2 + x^{2})}^{π} .$

$y = {(2 + x)}^{π} .$

Xem đáp án

41. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định D của hàm số $y = {(x^{2} - 3 x)}^{- 4}$ là

(0;3)

$D = ℝ \ \{0; 3\} .$

D = R

$D = (- \infty; 0) \cup (3; + \infty) .$

Xem đáp án

42. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định của hàm số $y = {(x^{2} - 4 x)}^{\frac{2019}{2020}}$ là

$(- \infty; 0] \cup [4; + \infty) .$

$(- \infty; 0) \cup (4; + \infty) .$

(0;4)

$ℝ \ \{0; 4\} .$

Xem đáp án

43. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định D của hàm số $y = {(3 - x)}^{0}$ là

$D = (- \infty; 3) .$

$D = (- \infty; 3] .$

$D = ℝ \ \{3\} .$

$D = ℝ .$

Xem đáp án

44. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định D của hàm số $y = {(\frac{x - 3}{x + 2})}^{- \sin \frac{π}{2}}$ là

$D = ℝ \ \{- 2; 3\} .$

$D = (- \infty, - 2) \cup [3, + \infty) .$

$D = ℝ \ \{3\} .$

$D = (- \infty; - 2) \cup (3; + \infty) .$

Xem đáp án

45. Trắc nghiệm

• 1 điểm • Không giới hạn

Tập xác định D của hàm số $y = x^{e} + {(x^{2} - 1)}^{π}$ là

$D = (- 1; 1) .$

$D = ℝ \ \{- 1; 1\} .$

$D = (1; + \infty) .$

$D = ℝ .$

Xem đáp án

46. Trắc nghiệm

• 1 điểm • Không giới hạn

Có bao nhiêu giá trị nguyên của tham số $m \in (- 50; 50)$ để hàm số $y = {(x^{2} - 2 x - m + 1)}^{\frac{1}{2}}$ có tập xác định R?

99.

49.

50.

100.

Xem đáp án

47. Trắc nghiệm

• 1 điểm • Không giới hạn

Biết tham số $m \in (a; b),$ với $a < b$ thì hàm số $y = {(x^{2} - 2 x - m^{2} + 5 m - 5)}^{\sqrt{3 + 2 \sqrt{2}}}$ có tập xác định là Giá trị tổng a + b là

-5

-3

Xem đáp án

48. Trắc nghiệm

• 1 điểm • Không giới hạn

Tất cả các giá trị thực của m để hàm số $y = {(x^{2} - 4 x + m)}^{\frac{2019}{2020}}$ xác định trên R là

$m > 4.$

$m < 4.$

$m \geq 4.$

$m \leq 4.$

Xem đáp án

49. Trắc nghiệm

• 1 điểm • Không giới hạn

Tất cả các giá trị thực của m để hàm số $y = {(x^{2} - 2 x - m)}^{\sqrt{2020}}$ xác định trên R là

$m > 1.$

$m > - 1.$

$m < 1.$

$m < - 1.$

Xem đáp án

50. Trắc nghiệm

• 1 điểm • Không giới hạn

Tất cả các giá trị thực của tham số m sao cho hàm số $y = {(x^{2} - m x + 1)}^{\sin \frac{π}{3}}$ có tập xác định R là

$- 2 \leq m \leq 2.$

$m < - 2 \lor m > 2.$

$- 1 < m < 1.$

$- 2 < m < 2.$

Xem đáp án

51. Trắc nghiệm

• 1 điểm • Không giới hạn

Tất cả các giá trị thực của m để hàm số $y = {(\frac{x^{2} + 2 m x + m + 2}{x^{2} + 3})}^{- \sqrt{2}}$ xác định trên R là

$- 1 < m < 2.$

$- 1 \leq m < 2.$

$- 2 < m < 2.$

$- 1 < m \leq 2.$

Xem đáp án

52. Trắc nghiệm

• 1 điểm • Không giới hạn

Phương trình tiếp tuyến của $(C) : y = x^{\frac{π}{2}}$ tại điểm $M_{0}$ có hoành độ $x_{0} = 1$ là

$y = \frac{π}{2} x + 1.$

$y = \frac{π}{2} x - \frac{π}{2} + 1.$

$y = π x - π + 1.$

$y = - \frac{π}{2} x + \frac{π}{2} + 1.$

Xem đáp án

53. Trắc nghiệm

• 1 điểm • Không giới hạn

Trên đồ thị của hàm số $y = x^{\frac{π}{2} + 1}$ lấy điểm $M_{0}$ có hoành độ $x_{0} = 2^{\frac{2}{π}} .$ Tiếp tuyến của (C) tại điểm $M_{0}$ có hệ số góc bằng

$π + 2.$

$2 π .$

$2 π - 1.$

Xem đáp án

54. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho các hàm số lũy thừa $y = x^{α}, y = x^{β}, y = x^{γ}$ có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?

Media VietJack

$γ > β > α .$

$β > γ > α .$

$β > α > γ .$

$α > β > γ .$

Xem đáp án

55. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho $α, β$ là các số thực. Đồ thị các hàm số $y = x^{α}, y = x^{β}$ trên khoảng $(0; + \infty)$ được cho trong hình vẽ bên. Khẳng định nào sau đây là đúng?