145 câu Chuyên đề Toán 12 Bài 3: Hàm số mũ - Hàm số logarit có đáp án
145 câu hỏi
Khẳng định nào sau đây sai?
Tìm đạo hàm của hàm số .
Tìm đạo hàm của hàm số .
Tìm đạo hàm của hàm số .
Cho hàm số . Giá trị f'(2) bằng
Cho hàm số . Giá trị của y'(1)bằng
Tìm a để hàm số nghịch biến trên R.
Hàm số nào sau đây đồng biến trên R?
Cho hàm số . Khẳng định nào sau đây đúng?
Hàm số đồng biến trên khoảng .
Hàm số nghịch biến trên khoảng .
Hàm số nghịch biến trên khoảng .
Hàm số đồng biến trên khoảng .
Cho hàm số . Khẳng định nào sau đây đúng?
Cho hàm số đạt cực trị tại x = 1 và đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng e. Giá trị của hàm số tại x = 2 là
y(2) = 1
y(2) = e
Cho hàm số , khẳng định nào sau đây đúng?
Cho hàm số , biết với . Giá trị của a + b bằng
2
7
4
1
Tìm đạo hàm của hàm số tại điểm x = 1.
f'(1) = 1
Tìm đạo hàm của hàm số .
Cho hàm số f(x) = ln x. Tìm đạo hàm của hàm số .
Cho hàm số . Khẳng định nào sau đây đúng?
Hàm số đạt cực trị tại
Cho hàm số . Khẳng định nào sau đây đúng?
Hàm số nào sau đây đồng biến trên R?
Các giá trị thực của tham số a để hàm số nghịch biến trên tập xác định là
a = 2
Với giá trị nào của tham số a thì hàm số đồng biến?
a = 1
a = 2
Cho a,b là hai số thực thỏa mãn . Mệnh đề nào sau đây là đúng?
Giá trị nhỏ nhất của hàm số trên đoạn là
Đối với hàm số . Khẳng định nào sau đây đúng?
Đạo hàm của hàm số là
Cho hàm số y = x sin x. Khẳng định nào sau đây đúng?
Hàm số đồng biến trên khi
Trong các hàm số sau đây, hàm số nào đồng biến?
Trong các hàm số sau, hàm số nào nghịch biến trong khoảng ?
Đạo hàm của hàm số là
Tìm đạo hàm của hàm số .
Cho hàm số . Khẳng định nào sau đây đúng?
Tìm đạo hàm của hàm số .
Cho hàm số . Đạo hàm f'(1) bằng
1
2
Tìm đạo hàm của hàm số
Tìm đạo hàm của hàm số .
Đạo hàm của hàm số trên tập xác định là
Nếu và thì
và
và
và
và
Tìm đạo hàm của hàm số .
Cho hàm số . Nghiệm của phương trình là
x = 0
x = 1
x = -1
x = ln 2
Tìm đạo hàm của hàm số .
Cho hàm số . Giá trị của là
Cho a,b là các số thực dương thỏa mãn và . Mệnh đề nào sau đây đúng?
Cho hàm số . Tính tổng , ta được kết quả
S = 2017
Giá trị nhỏ nhất của hàm số trên tập hợp các số tự nhiên là
-1283
Các giá trị của tham số m để hàm số đồng biến trên R là
Không tồn tại m
Tập hợp tất cả các giá trị của tham số thực m để hàm số đồng biến trên khoảng (-1;1) là
Tập xác định D của hàm số là
(1;2)
Điều kiện xác định D của hàm số là
Tìm tập xác định D của hàm số
Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số xác định với mọi ?
5
2
4
3
Tìm m để hàm số có tập xác định D = R.
Có tất cả bao nhiêu giá trị nguyên của tham số m nằm trong khoảng (-10;10) để hàm số có tập xác định D = R?
9
10
11
8
Có tất cả bao nhiêu giá trị nguyên của tham số m nằm trong khoảng (-10;10) để hàm số xác định trên khoảng ?
13
11
12
10
Tìm tập xác định D của hàm số .
Tìm tập xác định D của hàm số .
Tìm tập xác định D của hàm số .
Tìm tập xác định D của hàm số .
Tìm tập xác định D của hàm số .
Tìm tập xác định D của hàm số
Tìm tập xác định D của hàm số .
Cho hàm số . Các giá trị thực của tham số m để hàm số đã cho xác định với mọi là
Điều kiện xác định của phương trình là
Tập xác định D của hàm số là
Tìm tất cả các giá trị thực của tham số m để hàm số có tập xác định D = R.
hoặc
Hàm số có tập xác định là
Tập xác định của hàm số là
Tập xác định của hàm số là
Hàm số có tập xác định D = R khi
Tập xác định D của hàm số là
Tập xác định của hàm số là.
R
Cho ba số thực dương a,b,c khác 1. Đồ thị các hàm số được cho trong hình vẽ sau
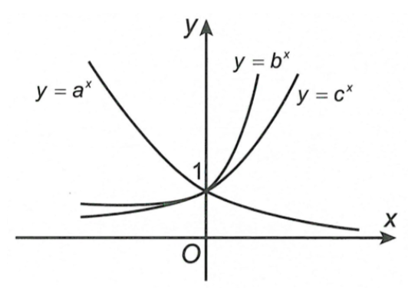
Mệnh đề nào đúng?
Từ các đồ thị , , đã cho ở hình vẽ sau:
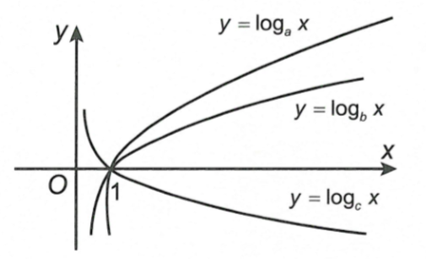
Khẳn định nào sau đây đúng?
Cho các hàm số , , có đồ thị như hình vẽ.
Chọn mệnh đề đúng?
Cho hàm số . Khẳng định nào sau đây sai?
Hàm số có tập xác định là .
Hàm số nghịch biến trên
Đồ thị hàm số có tiệm cận đứng là trục Oy.
Tìm phát biểu sai.
Đồ thị hàm số nằm hoàn toàn phía trên Ox.
Đồ thị hàm số luôn đi qua điểm A(0;1).
Đồ thị hàm số đối xứng nhau qua trục Ox.
Đồ thị hàm số đối xứng nhau qua trục Oy.
Cho đồ thị của ba hàm số , , như hình vẽ bên. Khẳng định nào sau đây đúng?
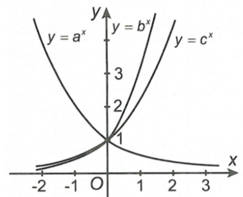
Hàm số nào có đồ thị như hình vẽ bên?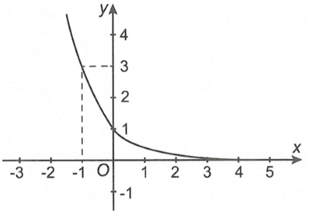
Trong các hình sau, hình nào là dạng đồ thị của hàm số ?
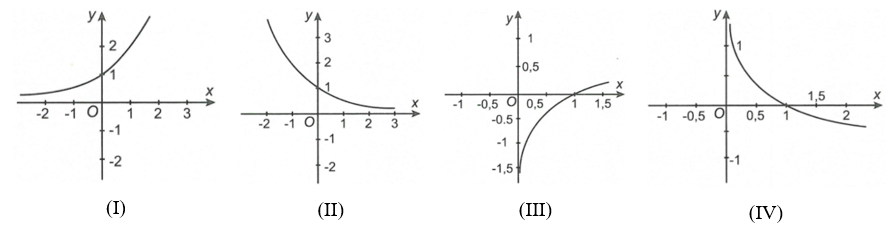
(I)
(II)
(III)
(IV)
Trong các hình sau, hình nào là dạng đồ thị của hàm số ?
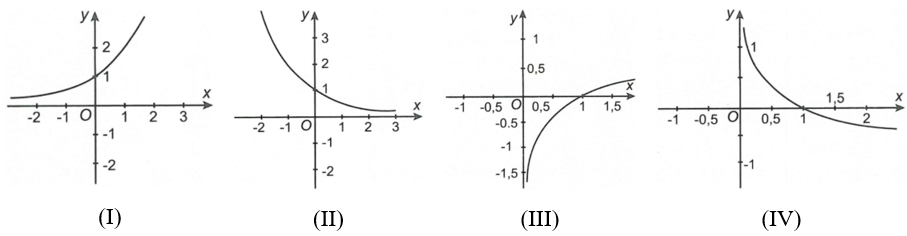
(I)
(II)
(IV)
(III)
Quan sát hình vẽ. Khẳng định nào sau đây là đúng?
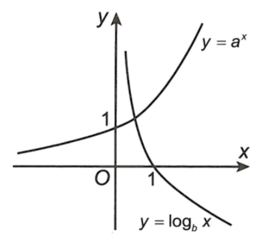
Cho hai hàm số có đồ thị lần lượt là và như hình vẽ bên. Khẳng định nào dưới đây đúng?
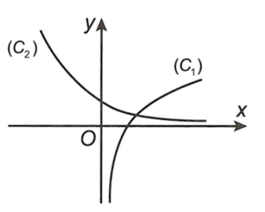
Cho các hàm số và có đồ thị như hình vẽ bên. Đường thẳng x = 7 cắt trục hoành, đồ thị hàm số và lần lượt tại H, M, N. Biết rằng . Mệnh đề nào sau đây là đúng?
a = 7b
a = 2b
Đường cong trong hình bên là đồ thị của một hàm số nào trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây?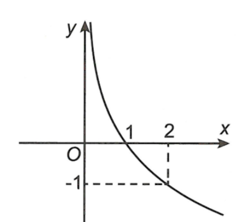
Với giá thị nào của a để hàm số có đồ thị là hình bên ?
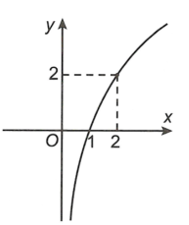
a = 2
Biết hàm số có đồ thị là hình bên. Khi đó, hàm số có đồ thị là hình nào trong bốn hình được liệt kê ở bốn A, B, C, D dưới đây?
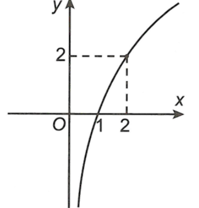
Hình 4
Hình 2
Hình 3
Hình 1
Giá trị lớn nhất của hàm số trên đoạn [-1;1]là
e
2e
0
Cho hàm số . Khi đó, hàm số có đồ thị là hình nào trong bốn hình được liệt kê ở bốn phương án A, B, C, D dưới đây?
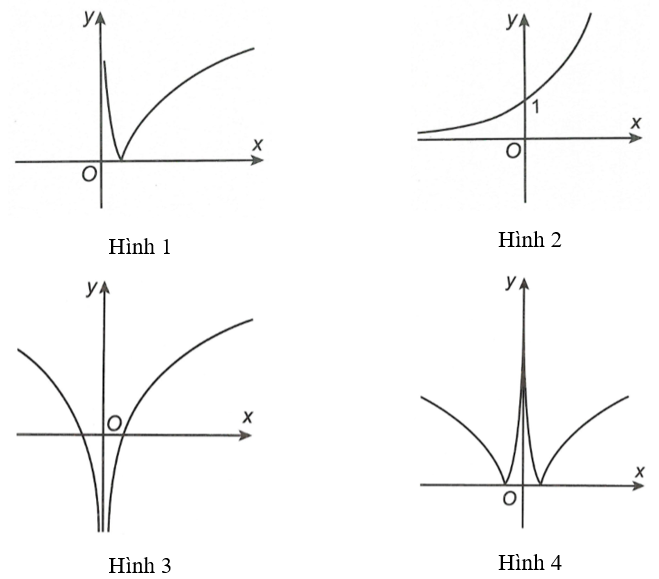
Hình 3
Hình 2
Hình 1
Hình 4
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên [-2;2]?
Hình bên là đồ thị của ba hàm số , , được vẽ trên cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?
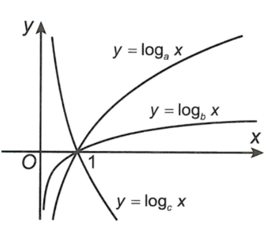
Cho hàm số . Tìm khẳng định sai.
Hàm số luôn nghịch biến trên R.
Đồ thị hàm số luôn cắt trục hoành tại điểm có hoành độ bằng 1.
Hàm số không có cực trị.
f(x) luôn nhỏ hơn 1 với mọi x dương.
Cho . Nếu a + b = 1thì f(a) + f(b) là
1
2
3
4
Cho hàm số . Nếu a + b = 3 thì có giá trị bằng
1
2
Hàm số có bao nhiêu điểm cực trị?
0
2
1
3
Cho ba số thực dương a,b,c khác 1. Đồ thị các hàm số , , được cho trong hình vẽ sau:
Mệnh đề nào dưới đây đúng?
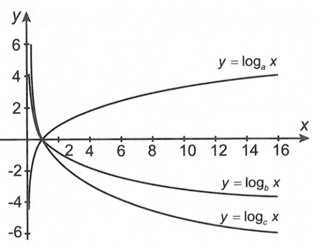
Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây?
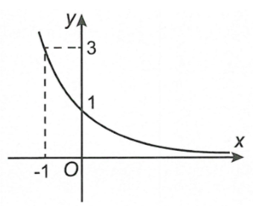
Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây?
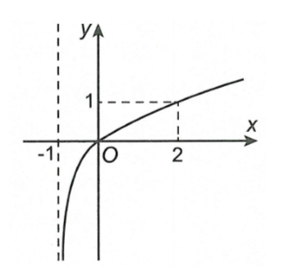
Cho hàm số có đồ thị Hình 1. Đồ thị Hình 2 là của hàm số nào dưới đây?
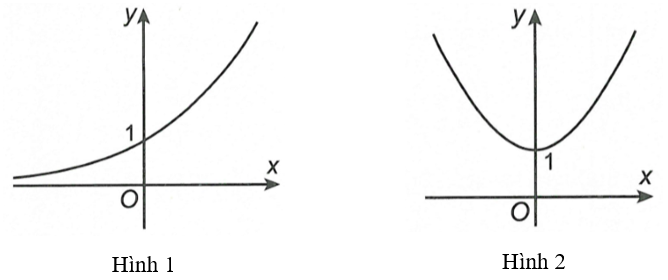
Cho hàm số có đồ thị (C). Hàm số nào sau đây có đồ thị đối xứng với (C)qua đường thẳng y = x?
Cho hàm số có đồ thị (C). Hàm số nào sau đây có đồ thị đối xứng với (C) qua đường thẳng y = x?
Cho hàm số có đồ thị (C). Hàm số nào sau đây có đồ thị đối xứng với (C) qua đường thẳng y = x?
Đối xứng qua trục hoành của đồ thị hàm số là đồ thị nào trong các đồ thị có phương trình sau đây?
Một người gửi tiết kiệm số tiền 80 000 000 đồng với lãi suất 6,9% một năm. Biết rằng tiền lãi hàng năm được cộng vào tiền gốc, hỏi sau 5 năm người đó rút được cả tiền gốc lẫn tiền lãi gần với con số nào sau đây?
105370000 đồng
111680000 đồng
107667000 đồng
116570000 đồng
Một người gửi ngân hàng 100 triệu với lãi suất 0,5% một tháng. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được cộng vào vốn ban đầu để tính lãi cho tháng tiếp theo. Sau ít nhất bao nhiêu tháng, người đó có nhiều hơn 125 triệu?
45 tháng
46 tháng
47 tháng
44 tháng
Bác Toản gửi số tiền 58 triệu đồng vào một ngân hàng theo hình thức lãi kép và ổn định trong 9 tháng thì lĩnh về được 61758000 đồng. Hỏi lãi suất ngân hàng hàng tháng là bao nhiêu? Biết rằng lãi suất không thay đổi trong thời gian gửi.
0.8%
0,6%
0,7%
0,5%
Để đủ tiền mua nhà, anh An vay ngân hàng 500 triệu theo phương thức trả góp với lãi suất 0,85% mỗi tháng. Nếu sau mỗi tháng, kể từ thời điểm vay, anh An trả nợ cho ngân hàng số tiền cố định là 10 triệu đồng bao gồm cả tiền lãi vay và tiền gốc. Biết phương thức trả lãi và gốc không thay đổi trong suốt quá trình anh An trả nợ. Hỏi sau bao nhiêu tháng anh trả hết nợ ngân hàng?
65
66
67
68
Bác An có 400 triệu đồng mang đi gửi tiết kiệm ở hai kì hạn khác nhau đều theo hình thức lãi kép. Bác gửi 200 triệu đồng theo kì hạn quý với lãi suất 2,1% một quý; 200 triệu còn lại bác gửi theo kì hạn tháng với lãi suất 0,73% một tháng. Sau khi gửi được đúng 1 năm, bác rút tất cả số tiền ở loại kì hạn theo quý và gửi theo tháng. Hỏi sau đúng 2 năm kể từ khi gửi tiền lần đầu, bác An thu được tất cả bao nhiêu tiền lãi? (kết quả làm tròn đến hàng phần nghìn).
75,304 triệu đồng
75,303 triệu đồng
470,656 triệu đồng
475,304 triệu đồng
Một người vay ngân hàng số tiền 350 triệu đồng, mỗi tháng trả góp 8 triệu đồng và lãi suất cho số tiền chưa trả là 0,79% một tháng. Kì trả đầu tiên là cuối tháng thứ nhất. Hỏi số tiền phải trả ở kì cuối là bao nhiêu để người này hết nợ ngân hàng? (làm tròn đến hàng nghìn)
2921000 đồng
7084000 đồng
2944000 đồng
7140000 đồng
Ông A vay dài hạn ngân hàng 300 triệu, với lãi suất 12% năm. Ông muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một năm kể từ ngày vay, ông bắt đầu hoàn nợ, hai lần hoàn nợ liên tiếp cách nhau đúng một năm, số tiền hoàn ở mỗi lần là như nhau và trả hết nợ sau đúng 4 năm kể từ ngày vay. Hỏi theo cách đó, số tiền m mà ông A sẽ phải trả cho ngân hàng trong mỗi lần hoàn nợ là bao nhiêu? Biết rằng lãi suất ngân hàng không thay đổi trong thời gian ông A hoàn nợ.
(triệu đồng)
(triệu đồng)
(triệu đồng)
( triệu đồng)
Một người mỗi đầu tháng gửi vào ngân hàng T triệu đồng với lãi suất kép 0,6% một tháng. Biết cuối tháng thứ 15 thì số tiền cả gốc lẫn lãi sẽ thu về là 10 triệu đồng. Hỏi số tiền T gần với số nào nhất trong các số sau đây?
535000 đồng
635000 đồng
613000 đồng
643000 đồng
Một huyện A có 100 000 dân. Với mức tăng dân số bình quân 1,8% năm thì sau ít nhất bao nhiêu năm nữa dân số sẽ vượt 150 000 dân.
22
23
27
28
Tỉ lệ tăng dân số hàng năm ở Việt Nam được duy trì ở mức 1,05%. Theo số liệu của Tổng cục Thống kê, dân số của Việt Nam năm 2014 là 90728900 người. Với tốc độ tăng dân số như thế thì vào năm 2030, dân số của Việt Nam là:
106118331 người
198049810 người
107232574 người
108358516 người
Trong vật lý, sự phân rã của các chất phóng xạ được biểu diễn bởi công thức: , trong đó là khối lượng ban đầu của chất phóng xạ (tại thời điểm t = 0); T là chu kì bán rã (tức là khoảng thời gian để một nửa khối lượng chất phóng xạ bị biến thành chất khác). Chu kì bán rã của Cabon là khoảng 5730 năm. Cho trước mẫu Cabon có khối lượng 100g. Hỏi sau khoảng thời gian t thì khối lượng còn bao nhiêu gam?
Cường độ ánh sáng đi qua môi trường khác không khí (chẳng hạn sương mù, nước,…) sẽ giảm dần tùy thuộc độ dày của môi trường và hằng số gọi là khả năng hấp thu của môi trường, tùy thuộc môi trường thì khả năng hấp thu tính theo công thức với x là độ dày của môi trường đó và được tính bằng đơn vị mét. Biết rằng nước biển có . Hãy tính cường độ ánh sáng giảm đi bao nhiêu khi từ độ sâu 2m xuống đến 20m?
Một người gửi vào ngân hàng 50 triệu đồng thời hạn 15 tháng, lãi suất 0,6% tháng (lãi kép). Khi hết kỳ hạn thì số tiền người đó nhận được là
55,664000 triệu
54,694000 triệu
55,022000 triệu
54,368000 triệu
Một người gửi ngân hàng 50 triệu đồng theo hình thức lãi kép kỳ hạn 1 năm với lãi suất 7% mỗi năm. Hỏi sau 4 năm người đó có bao nhiêu tiền cả gốc và lãi?
70,13 triệu đồng
65,54 triệu đồng
61,25 triệu đồng
65,53 triệu đồng
Một học sinh A khi 15 tuổi được hưởng tài sản thừa kế 200 000 000 đồng. Số tiền này được bảo quản trong một ngân hàng B với kì hạn thanh toán một năm và học sinh A chỉ nhận được số tiền này khi 18 tuổi. Biết rằng khi 18 tuổi, số tiền mà học sinh A được nhận sẽ là 231525000 đồng. Vậy lãi suất kì hạn 1 năm của ngân hàng B là bao nhiêu?
8%
7%
6%
5%
Một chiếc ô tô mới mua năm 2016 với giá 800 triệu đồng. Cứ sau mỗi năm, giá chiếc ô tô này bị giảm 5%. Hỏi đến năm 2020, giá tiền chiếc ô tô này còn khoảng bao nhiêu?
651605000 đồng
685900000 đồng
619024000 đồng
760000000 đồng
Ông An gửi vào ngân hàng 60 triệu đồng theo hình thức lãi kép. Lãi suất ngân hàng là 8% trên năm. Sau 5 năm ông An tiếp tục gửi thêm 60 triệu đồng nữa. Hỏi sau 10 năm kể từ lần gửi đầu tiên ông An đến rút toàn bộ tiền gốc và tiền lãi được là bao nhiêu? (Biết lãi suất không thay đổi qua các năm ông gửi tiền).
231,815 (triệu đồng)
197,201 (triệu đồng)
217,695 (triệu đồng)
190,271 (triệu đồng)
Một người vay ngân hàng 90000000 đồng theo hình thức trả góp trong 3 năm. Mỗi tháng người đó phải trả số tiền bằng nhau. Giả sử lãi suất trong toàn bộ quá trình trả nợ không đổi là 0,8% trên tháng. Tổng số tiền người đó phải trả trong toàn bộ quá trình trả nợ là
103320000 đồng
101320000 đồng
105320000 đồng
103940000 đồng
Anh Minh gửi vào ngân hàng 50 triệu đồng với lãi suất 0,6% tháng. Sau mỗi tháng, anh Minh đến ngân hàng rút mỗi tháng 3 triệu đồng để chi tiêu cho đến khi hết tiền thì thôi. Sau một số tròn tháng thì anh Minh rút hết tiền cả gốc lẫn lãi. Biết trong suốt thời gian đó, ngoài số tiền rút mỗi tháng, anh Minh không rút thêm một đồng nào kể cả gốc lẫn lãi và lãi suất không đổi. Vậy tháng cuối cùng anh Minh sẽ rút được số tiền là bao nhiêu (làm tròn đến đồng)?
1840270 đồng
3000000 đồng
1840269 đồng
1840268 đồng
Bác Tuấn gửi tiết kiệm 75 triệu đồng vào ngân hàng theo kì hạn một quý với lãi suất 1,77% một quý. Nếu Bác Tuấn không rút lãi ở tất cả các định kì thì sau 3 năm Bác Tuấn nhận được số tiền cả vốn lẫn lãi là bao nhiêu? Biết rằng hết một kì hạn lãi sẽ được cộng vào vốn để tính lãi trong kì tiếp theo.
90930000 đồng
92690000 đồng
92576000 đồng
80486000 đồng
Một sinh viên muốn có 12 triệu đồng để mua laptop nên mỗi tháng gửi vào ngân hàng 250000 đồng với lãi suất 0,72% một tháng. Hỏi sau bao nhiêu tháng anh ta đủ tiền mua laptop?
41
36
42
37
Cô Ngọc vay ngân hàng một số tiền với lãi suất 1% mỗi tháng. Cô ấy muốn hoàn nợ cho ngân hàng theo cách: Sau đúng một tháng kể từ ngày cho vay, cô ấy bắt đầu hoàn nợ, hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi tháng là 5 triệu đồng và cô ấy trả hết nợ sau đúng 5 năm kể từ ngày vay (số tiền hoàn nợ tháng cuối cùng có thể ít hơn 5 triệu đồng). Biết rằng mỗi tháng ngân hàng chỉ tính lãi trên số dư nợ thực tế của tháng đó. Hỏi số tiền mà cô Ngọc vay ngân hàng là số nào trong các số dưới đây?
224 triệu đồng
222 triệu đồng
221 triệu đồng
225 triệu đồng
Để đủ tiền mua nhà, anh An vay ngân hàng 500 triệu đồng theo phương thức trả góp với lãi suất 0,85% mỗi tháng. Nếu sau mỗi tháng, kể từ thời điểm vay, anh An trả nợ cho ngân hàng số tiền cố định là 10 triệu đồng bao gồm cả tiền lãi vay và tiền gốc. Biết rằng phương thức trả lãi và gốc không thay đổi trong suốt quá trình anh An trả nợ. Hỏi sau bao nhiêu tháng thì anh trả hết nợ ngân hàng?
68
66
65
67
Một người vay ngân hàng 200 triệu đồng với lãi suất 0,6% một tháng theo thỏa thuận: Sau đúng một tháng kể từ ngày vay thì ông bắt đầu trả nợ và đều đặn cứ mỗi tháng người đó sẽ trả cho ngân hàng 9 triệu đồng cho đến khi hết nợ (biết rằng, tháng cuối cùng có thể trả dưới 9 triệu đồng). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng?
24
23
22
25
Ông Tuấn đầu tư 500 triệu đồng để mua xe ô tô chở khách. Sau khi mua, thu nhập bình quân mỗi tháng được 10 triệu đồng (sau khi trừ đi các khoản chi phí khác). Tuy nhiên mỗi năm giá trị xe lại giảm 10% so với năm trước đó. Tổng số tiền lãi sau 4 năm kinh doanh của ông Tuấn bằng bao nhiêu?
480 triệu đồng
308,05 triệu đồng
328,05 triệu đồng
Lỗ 171,95 triệu đồng
Anh Hòa gửi ngân hàng 3350000 đồng, theo phương thức lãi đơn với lãi suất 0,4% trên nửa năm. Hỏi ít nhất bao lâu anh rút được cả vốn lẫn lãi là 4020000 đồng?
5 năm
30 tháng
3 năm
24 tháng
Một khách hàng gửi tiết kiệm 64 triệu đồng, với lãi suất 0,85% một tháng. Hỏi người đó phải mất ít nhất mấy tháng để được số tiền cả gốc lẫn lãi không dưới 72 triệu đồng?
13
14
15
18
Anh Ngọc muốn vay ngân hàng 200 triệu đồng theo phương thức trả góp (trả tiền vào cuối tháng) với lãi suất 0,75% mỗi tháng. Hỏi hàng tháng, anh Ngọc phải trả số tiền là bao nhiêu (làm tròn đến nghìn đồng) để sau đúng 2 năm thì trả hết nợ ngân hàng?
9236000 đồng
9137000 đồng
9970000 đồng
9971000 đồng
Một người nhận hợp đồng dài hạn làm việc cho một công ty với mức lương khởi điểm của mỗi tháng trong ba năm đầu tiên là 6 triệu đồng/tháng. Tính từ ngày đầu làm việc, cứ sau đúng ba năm liên tiếp thì tăng lương 10% so với mức lương một tháng người đó đang hưởng. Nếu tính theo hợp đồng thì tháng đầu tiên của năm thứ 16 người đó nhận được mức lương là bao nhiêu?
(triệu đồng)
(triệu đồng)
(triệu đồng)
(triệu đồng)
Một người cứ đầu tháng đều gửi vào ngân hàng một khoản tiền T theo hình thức lãi kép với lãi suất 0,6% mỗi tháng. Đến cuối tháng thứ 15 thì người đó có số tiền là 10 triệu đồng. Hỏi số tiền T gần với số tiền nào nhất trong các số sau?
535000 đồng
635000 đồng
643000 đồng
613000 đồng
Một người nhận hợp đồng dài hạn làm việc trong một công ty với lương năm đầu là 72 triệu đồng, cứ sau 3 năm thì tăng lương 10%. Nếu tính theo hợp đồng thì sau đúng 21 năm, người đó nhận được tổng số tiền của công ty là
(triệu đồng)
(triệu đồng)
(triệu đồng)
(triệu đồng)
Một người vay ngân hàng 200 triệu đồng với lãi suất 0,6% một tháng theo hình thức lãi kép với thỏa thuận: sau đúng một tháng kể từ ngày vay thì ông bắt đầu trả nợ và đều đặn cứ mỗi tháng người đó sẽ trả cho ngân hàng 9 triệu đồng cho đến khi hết nợ (biết rằng, tháng cuối cùng có thể trả dưới 9 triệu đồng). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng?
25
24
22
23
Một người gửi tiền tiết kiệm vào một ngân hàng với lãi suất 6,1% năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì sau mỗi năm số tiền lãi sẽ được nhập vào gốc và tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó thu được số tiền lãi ít nhất bằng số tiền gửi ban đầu, giả định trong thời gian này lãi suất không thay đổi và người đó không rút tiền ra?
12 năm
11 năm
10 năm
13 năm
Một khách hàng gửi ngân hàng 20 triệu đồng, kì hạn 3 tháng, với lãi suất 0,65% một tháng theo phương thức lãi kép. Hỏi sau bao lâu vị khách này mới có số tiền lãi nhiều hơn số tiền gốc ban đầu gửi ngân hàng? Giả sử người đó không rút lãi ở tất cả các định kì.
8 năm 11 tháng
19 tháng
18 tháng
9 năm
Một người vay ngân hàng số tiền 400 triệu đồng, mỗi tháng trả góp 10 triệu đồng và lãi suất cho số tiền chưa trả là 1% mỗi tháng. Kì trả đầu tiên là cuối tháng thứ nhất. Biết lãi suất không đổi trong suốt quá trình gửi, hỏi số tiền còn phải trả ở kì cuối là bao nhiêu để người này hết nợ ngân hàng? (làm tròn đến hàng nghìn).
2921000 đồng
3387000 đồng
2944000 đồng
7084000 đồng
Mỗi tháng bà A gửi vào ngân hàng một khoản tiền không đổi với lãi suất cố định là 0,4% mỗi tháng. Ba năm rưỡi kể từ ngày gửi khoản tiền đầu tiên, bà A rút toàn bộ số tiền để mua xe. Số tiền nhận về lấy đến hàng nghìn là 91635000 đồng. Hỏi khoản tiền gửi mỗi tháng của bà A là bao nhiêu?
2000000 đồng
1800000 đồng
1500000 đồng
2500000 đồng
Dân số thế giới cuối năm 2010, ước tính 7 tỉ người. Hỏi với mức tăng trưởng dân số 1,5% mỗi năm thì cuối năm 2020 dân số thế giới là bao nhiêu?
8,12 tỉ người
8,05 tỉ người
8 tỉ người
8,10 tỉ người
Một khu rừng có trữ lượng gỗ mét khối. Biết tốc độ sinh trưởng của các cây trong rừng đó là 4% mỗi năm. Hỏi sau 10 năm khu rừng đó có số mét khối gỗ gần nhất với số nào?
Để đo độ phóng xạ của một chất phóng xạ người ta dùng máy đếm xung. Khi chất này phóng xạ ra các hạt , các hạt này đập vào máy làm trong máy xuất hiện một xung điện và bộ đếm tăng thêm 1 đơn vị. Ban đầu máy đếm được 960 xung trong một phút nhưng sau đó 3 giờ thì chỉ còn 120 xung trong một phút (trong cùng điều kiện). Hỏi chu kì bán rã của chất này là bao nhiêu giờ?
1 giờ
2 giờ
0,5 giờ
1,5 giờ
Áp suất không khí P (đo bằng milimet thủy ngân, kí hiệu mmHg) suy giảm mũ so với độ cao x (đo bằng mét), tức là P giảm theo công thức: , trong đó là áp suất ở mực nước biển x = 0, i là hệ số suy giảm. Biết rằng, ở độ cao 1000m thì áp suất của không khí là 672,72 mmHg. Hỏi áp suất của không khí ở độ cao 12km bằng bao nhiêu? (các kết quả giữ lại sau dấu thập phân 7 chữ số)
178,8176855
176,8176855
177,8176855
175,8176855
Người ta thả một số lá bèo vào một hồ nước, sau 10 giờ số lượng lá bèo sẽ sinh sôi kín cả mặt hồ. Biết rằng sau mỗi giờ số lượng lá đều tăng gấp 10 lần số lượng lá bèo trước đó và tốc độ tăng không đổi. Hỏi sau khoảng thời gian bao lâu số lượng lá bèo phủ kín tối thiểu một phần tư hồ?
(giờ)
(giờ)
(giờ)
(giờ)
Chu kì bán rã của nguyên tố phóng xạ ponoli 210 là 138 ngày (nghĩa là sau 138 ngày khối lượng của nguyên tố đó chỉ còn một nửa). Thời gian phân rã phóng xạ ponoli 210 để từ 20 gam còn lại gam gần đúng với đáp án nào nhất?
Khoảng 18 năm
Khoảng 21 năm
Khoảng 19 năm
Khoảng 20 năm




