56 bài tập Tính xác suất có điều kiện bằng công thức (có lời giải) - Đề 2

Một khu dân cư có \(85\% \) các hộ gia đình sử dụng điện để đun nước. Hơn nữa, có \(21\% \) các hộ gia đình sử dụng ấm điện siêu tốc. Chọn ngẫu nhiên một hộ gia đình, tính xác suất hộ đó sử dụng ấm điện siêu tốc, biết hộ đó sử dụng điện để đun nước.

Một hộp có 20 viên bi trắng và 10 viên bi đen, các viên bi có cùng kích thước và khó́i lượng. Bạn Bỉnh lấy ngẫu nhiên một viên bi trong hộp, không trả lại. Sau đơ bạn An lấy ngẫu nhiên một viên bi trong hộp đó.

Gọi \(A\) là biến cố: "An lấy được viên bi trắng"; \(B\) là biến cố: "Bình lấy được viên bi trắng".

Tính \(P(A\mid B)\) bằng định nghĩa và bằng công thức tính \(P(A\mid B)\) ở trên.

Một hộp có 20 viên bi trắng và 10 viên bi đen, các viên bi có cùng kích thước và khó́i lượng. Bạn Bỉnh lấy ngẫu nhiên một viên bi trong hộp, không trả lại. Sau đơ bạn An lấy ngẫu nhiên một viên bi trong hộp đó.

Gọi \(A\) là biến cố: "An lấy được viên bi trắng"; \(B\) là biến cố: "Bình lấy được viên bi trắng".

Tính \(P(A\mid \bar B)\) bằng định nghĩa và bằng công thức.

Từ công thức tính \(P(A\mid B)\) ở trên, chứng minh rằng nếu \(A\) và \(B\) là hai biến cố độc lập với \(P(A) > 0,P(B) > 0\) thì \(P(A\mid B) = P(A)\) và \(P(B\mid A) = P(B)\).

Từ định nghĩa xác suất có điều kiện và định nghĩa về tính độc lập của hai biến cố, hãy chứng tỏ rằng nếu \(A\) và \(B\) là hai biến cố độc lập thì \(P(A\mid B) = P(A)\) và \(P(B\mid A) = P(B)\).

Chứng tỏ rằng nếu A và B là hai biến cố độc lập thì: \(P(\bar A\mid B) = P(\bar A)\) và \(P(A\mid \bar B) = P(A)\)

Một nhóm học sinh tham gia một kì thi Olympic Tin học của trường, trong đó có 5 học sinh lớp 12 A . Sau khi chấm điểm, có 3 học sinh lớp 12 A đạt giải. Chọn ngẫu nhiên 1 học sinh trong nhóm học sinh trên. Tính xác suất chọn được học sinh đạt giải, biết rằng học sinh đó thuộc lớp 12 A .

Một hộp có 3 quả bóng màu xanh, 4 quả bóng màu đỏ; các quả bóng có kích thước và khối lượng như nhau. Lấy bóng ngẫu nhiên hai lần liên tiếp, trong đó mỗi lần lấy ngẫu nhiên một quả bóng trong hộp, ghi lại màu của quả bóng lấy ra và bỏ lại quả bóng đó vào hộp. Xét các biến cố:

A: "Quả bóng màu xanh được lấy ra ở lần thứ nhất";

\(B\) : "Quả bóng màu đỏ được lấy ra ở lần thứ hai".

Tính các xác suất \({\rm{P}}(A),{\rm{P}}(A\mid B),{\rm{P}}(A\mid \bar B),{\rm{P}}(B),{\rm{P}}(B\mid A),{\rm{P}}(B\mid \bar A)\).

Một hộp có 3 quả bóng màu xanh, 4 quả bóng màu đỏ; các quả bóng có kích thước và khối lượng như nhau. Lấy bóng ngẫu nhiên hai lần liên tiếp, trong đó mỗi lần lấy ngẫu nhiên một quả bóng trong hộp, ghi lại màu của quả bóng lấy ra và bỏ lại quả bóng đó vào hộp. Xét các biến cố:

A: "Quả bóng màu xanh được lấy ra ở lần thứ nhất";

\(B\) : "Quả bóng màu đỏ được lấy ra ở lần thứ hai".

Chứng minh rằng \(A\), \(B\) là hai biến cố độc lập.

Một hộp có 5 viên bi cùng kích thước và khối lượng, trong đó có 3 viên bi màu đỏ và 2 viên bi màu xanh. Lấy ngẫu nhiên lần lượt 2 viên bi và không hoàn lại. Tính xác suất để lấy được viên bi thứ hai có màu xanh, biết rằng viên bi thứ nhất có màu đỏ.

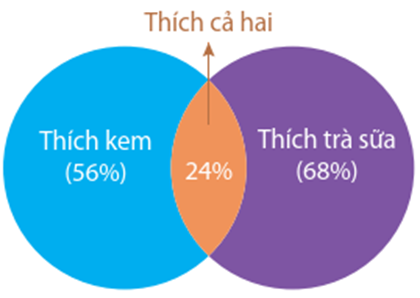
Trong cuộc khảo sát trên một nhóm học sinh gồm các bạn thích trà sữa hoặc kem, người ta có được kết quả sau: Có \(56\% \) số học sinh thích kem, \(68\% \) số học sinh thích trà sữa, \(24\% \) số học sinh thích cả trà sửa và kem (Hình 6.2). Chọn ngẫu nhiên một bạn học sinh trong nhóm được khảo sát này. Tính xác suất để chọn được học sinh thích kem, biết rằng học sinh đó thích trà sữa.

Một công ty vừa ra mắt sản phẩm \(X\) và tổ chức ngày trải nghiệm sản phẩm. Họ thống kê được trong 200 người đến tham quan ngày trải nghiệm có 60 người là nam giới và 140 người là nữ giới. Trong số những người được thống kê này, có 120 người mua sản phẩm X , gồm 40 khách hàng nam và 80 khách hàng nữ, còn lại là không mua sản phẩm X. Chọn ngẫu nhiên một người trong số 200 người được thống kê. Tính xác suất để người này mua sản phẩm \(X\), biết rằng người được chọn là nữ giới (làm tròn kết quả đến hàng phần trăm).

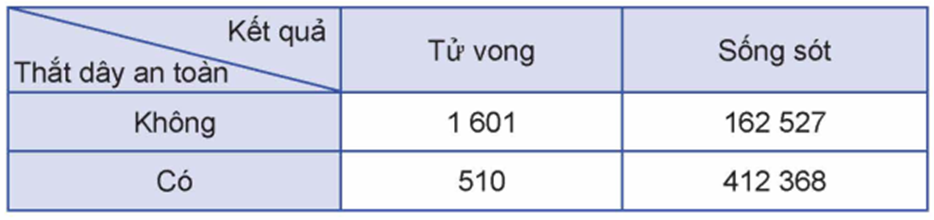
(Bảng dữ liệu thống kê \(2 \times 2\) ) Một viện nghiên cứu về an toàn giao thông muốn tìm hiểu về mối quan hệ giữa việc thắt dây an toàn khi lái xe và nguy cơ tử vong của người lái xe khi xảy ra tai nạn giao thông. Giả sử viện đã xem xét 577006 vụ tai nạn giao thông ô tô và việc thắt dây an toàn của người lái xe khi xảy ra tai nạn giao thông. Kết quả cho thấy:

- Trong số những người lái xe có thắt dây an toàn, có 510 người tử vong và 412368 người sống sót;

- Trong số những người lái xe không thắt dây an toàn, có 1601 người tử vong và 162527 người sống sót.

Kết quả trên được trình bày dưới dạng bảng gồm 2 dòng và 2 cột như dưới đây, được gọi là bảng dữ liệu thống kê \(2 \times 2\) :

Chọn ngẫu nhiên một người lái xe trong số 577006 người bị tai nạn giao thông.

Tính xác suất để người lái xe đó tử vong khi xảy ra tai nạn giao thông trong trường hợp không thắt dây an toàn.

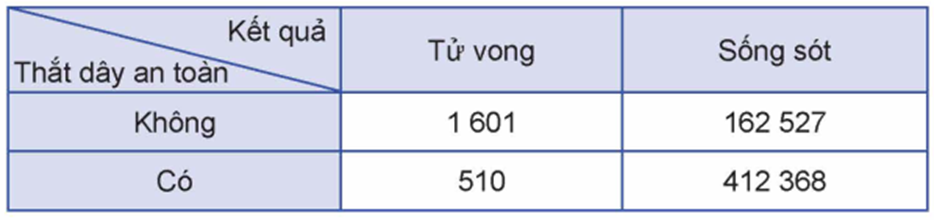
(Bảng dữ liệu thống kê \(2 \times 2\) ) Một viện nghiên cứu về an toàn giao thông muốn tìm hiểu về mối quan hệ giữa việc thắt dây an toàn khi lái xe và nguy cơ tử vong của người lái xe khi xảy ra tai nạn giao thông. Giả sử viện đã xem xét 577006 vụ tai nạn giao thông ô tô và việc thắt dây an toàn của người lái xe khi xảy ra tai nạn giao thông. Kết quả cho thấy:

- Trong số những người lái xe có thắt dây an toàn, có 510 người tử vong và 412368 người sống sót;

- Trong số những người lái xe không thắt dây an toàn, có 1601 người tử vong và 162527 người sống sót.

Kết quả trên được trình bày dưới dạng bảng gồm 2 dòng và 2 cột như dưới đây, được gọi là bảng dữ liệu thống kê \(2 \times 2\) :

Chọn ngẫu nhiên một người lái xe trong số 577006 người bị tai nạn giao thông.

Tính xác suất để người lái xe đó tử vong khi xảy ra tai nạn giao thông trong trường hợp có thắt dây an toàn.

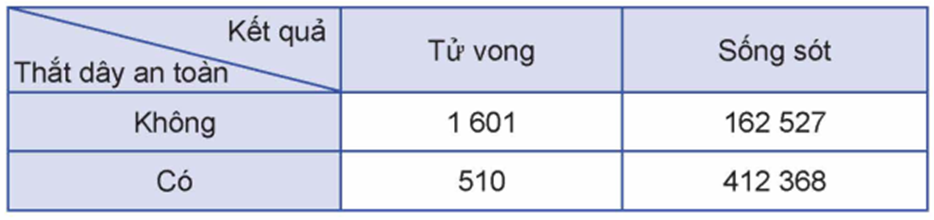
(Bảng dữ liệu thống kê \(2 \times 2\) ) Một viện nghiên cứu về an toàn giao thông muốn tìm hiểu về mối quan hệ giữa việc thắt dây an toàn khi lái xe và nguy cơ tử vong của người lái xe khi xảy ra tai nạn giao thông. Giả sử viện đã xem xét 577006 vụ tai nạn giao thông ô tô và việc thắt dây an toàn của người lái xe khi xảy ra tai nạn giao thông. Kết quả cho thấy:

- Trong số những người lái xe có thắt dây an toàn, có 510 người tử vong và 412368 người sống sót;

- Trong số những người lái xe không thắt dây an toàn, có 1601 người tử vong và 162527 người sống sót.

Kết quả trên được trình bày dưới dạng bảng gồm 2 dòng và 2 cột như dưới đây, được gọi là bảng dữ liệu thống kê \(2 \times 2\) :

Chọn ngẫu nhiên một người lái xe trong số 577006 người bị tai nạn giao thông.

So sánh hai xác suất ở câu \(a\) và câu b rồi rút ra kết luận.

Để thử nghiệm tác dụng điều trị bệnh mất ngủ của hai loại thuốc \(X\) và thuốc \(Y\), người ta tiến hành thử nghiệm trên 4000 người bệnh tình nguyện. Kết quả được cho trong bảng thống kê \(2 \times 2\) sau:

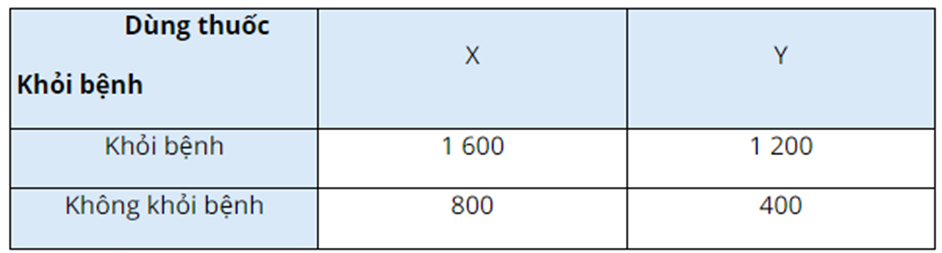
Chọn ngẫu nhiên 1 người bệnh tham gia tình nguyện thử nghiệm thuốc.

Tính xác suất để người đó khỏi bệnh nếu biết người bệnh đó uống thuốc \(X\).

Để thử nghiệm tác dụng điều trị bệnh mất ngủ của hai loại thuốc \(X\) và thuốc \(Y\), người ta tiến hành thử nghiệm trên 4000 người bệnh tình nguyện. Kết quả được cho trong bảng thống kê \(2 \times 2\) sau:

Chọn ngẫu nhiên 1 người bệnh tham gia tình nguyện thử nghiệm thuốc.

Tính xác suất để người bệnh đó uống thuốc \(Y\), biết rằng người đó khỏi bệnh.

Một công ty dược phẩm muốn so sánh tác dụng điều trị bệnh \(X\) của hai loại thuốc M và N . Công ty đã tiến hành thử nghiệm với 4000 bệnh nhân mắc bệnh X trong đó 2400 bệnh nhân dùng thuốc \({\rm{M}},1600\) bệnh nhân còn lại dùng thuốc N . Kết quả được cho trong bảng dữ liệu thống kê \(2 \times 2\) như sau: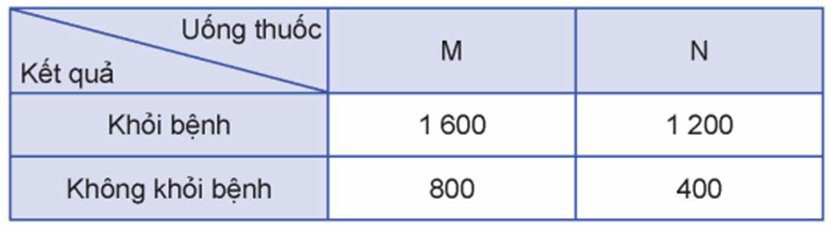  

Chọn ngẫu nhiên một bệnh nhân trong số 4000 bệnh nhân thử nghiệm sau khi uống thuốc. Tính xác suất để bệnh nhân đó

uống thuốc M , biết rằng bệnh nhân đó khỏi bệnh;

Một công ty dược phẩm muốn so sánh tác dụng điều trị bệnh \(X\) của hai loại thuốc M và N . Công ty đã tiến hành thử nghiệm với 4000 bệnh nhân mắc bệnh X trong đó 2400 bệnh nhân dùng thuốc \({\rm{M}},1600\) bệnh nhân còn lại dùng thuốc N . Kết quả được cho trong bảng dữ liệu thống kê \(2 \times 2\) như sau:  

Chọn ngẫu nhiên một bệnh nhân trong số 4000 bệnh nhân thử nghiệm sau khi uống thuốc. Tính xác suất để bệnh nhân đó

uống thuốc N , biết rằng bệnh nhân đó không khỏi bệnh.

Một hộp kín đựng 20 tấm thẻ giống hệt nhau đánh số từ 1 đến 20 . Một người rút ngẫu nhiên ra một tấm thẻ từ trong hộp. Người đó được thông báo rằng thẻ rút ra mang số chẵn. Tính xác suất để người đó rút được thẻ số 10 .

Một doanh nghiệp trước khi xuất khẩu áo sơ mi trong lô hàng \(S\) phải qua hai lần kiểm tra chất lượng sản phẩm, nếu cả hai lần đều đạt thì chiếc áo trong lô hàng đó mới đủ tiêu chuẩn xuất khẩu. Biết rằng bình quân \(98\% \) sản phẩm làm ra qua được lần kiểm tra thứ nhất và \(95\% \) sån phẩm qua được lần kiểm tra thứ nhất sẽ tiếp tục qu được lần kiểm tra thứ hai. Chọn ra ngẫu nhiên một chiếc áo sơ mi trong lô hàng . Tính xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu.

Một lô sản phẩm có 25 sản phẩm, trong đó có 8 sản phẩm chất lượng thấp. Lấy liên tiếp 2 sản phẩm trong lô sàn phẩm trên, trong đó sản phẩm lấy ra ở lần thứ nhất không được bỏ lại vào lô sản phẩm. Tính xác suất để cả hai sản phẩm được lấy ra đều có chất lượng thấp.

Cho hai xúc xắc cân đối và đồng chất. Gieo lần lượt từng xúc xắc trong hai xúc xắc đó. Tính xác suất để tổng số chấm xuất hiện trên hai xúc xắc bằng 6 , biết rằng xúc xắc thứ nhất xuất hiện mặt 4 chấm

Một doanh nghiệp trước khi xuất khẩu áo sơ mi phải qua hai lần kiểm tra chất lượng sản phẩm, nếu cả hai lần đều đạt thì chiếc áo đó mới đủ tiêu chuẩn xuất khẩu. Biết rằng bình quân  sản phẩm làm ra qua được lần kiểm tra thứ nhất và  sản phẩm qua được lần kiểm tra thứ nhất sẽ tiếp tục qua được lần kiểm tra thứ hai. Tính xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu.

Một lô sản phẩm có 20 sản phẩm, trong đó có 5 sản phẩm chất lượng thấp. Lấy liên tiếp 2 sản phẩm trong lô sản phẩm trên, trong đó sản phẩm lấy ra ở lần thứ nhất không được bỏ lại vào lô sản phẩm. Tính xác suất để cả hai sản phẩm được lấy ra đều có chất lượng thấp.

Trong một khu phố có 100 nhà, tại đó có 60 nhà gắn biển số chẵn và 40 nhà gắn biển số lẻ. Bên cạnh đó, có 50 nhà gắn biển số chẳn và 20 nhà gắn biển số lẻ đều có ô tô. Chọn ngẫu nhiên một nhà trong khu phố đó.

a) Tính xác suất nhà được chọn có ô tô, biết rằng nhà đó gắn biển số chẵn.

b) Tính xác suất nhà được chọn gắn biển số lẻ, biết rằng nhà đó có ô tô.

Một phòng học môn Tin học có 40 máy tính được đánh số từ 1 đến 40 , các máy cùng loại và cùng màu, mỗi máy được đánh một số khác nhau. Trong phòng học đó, xác suất chọn được một máy tính đã cài đặt phần mềm lập trình Python được đánh số chẵn và được đánh số lẻ lần lượt là 0,375 và 0,45 . Bạn Nam chọn ngẫu nhiên một máy tính trong phòng học đó.

a) Tính xác suất bạn Nam chọn được máy tính đã cài đặt phần mềm lập trình Python, biết rằng máy tính đó được đánh số lẻ.

b) Tính xác suất bạn Nam chọn được máy tính đánh số chẵn, biết rằng máy tính đó đã cài đặt phần mềm lập trình Python.

Trong kì kiểm tra môn Toán của một trường trung học phổ thông có 200 học sinh tham gia, trong đó có 95 học sinh nam và 105 học sinh nữ. Khi công bố kết quả của kì kiểm tra đó, có 50 học sinh đạt điểm giỏi, trong đó có 24 học sinh nam và 26 học sinh nữ. Chọn ra ngẫu nhiên một học sinh trong số 200 học sinh đó. Tính xác suất để học sinh được chọn ra đạt điểm giỏi, biết rằng học sinh đó là nữ (làm tròn kết quả đến hàng phần trăm).

Một lớp học có 17 học sinh nữ và 13 học sinh nam. ở lớp học đó, có 3 học sinh tên là Thanh, trong đó có 1 học sinh nữ và 2 học sinh nam. Thầy giáo gọi ngẫu nhiên một học sinh lên bảng. Xét hai biến cố sau:

A: "Học sinh được gọi lên bảng có tên là Thanh";

B: "Học sinh được gọi lên bảng là học sinh nữ".

Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được tính như thế nào?

Trong một đợt thi chứng chì hành nghề có 160 cán bộ tham gia, trong đó có 84 nam và 76 nữ. Khi công bố kết quả của kì kiểm tra đó, có 59 cán bộ đạt loại giỏi, trong đó có 30 cán bộ nam và 29 cán bộ nữ. Chọn ra ngẫu nhiên một cán bộ. Tính xác suất để cán bộ được chọn ra đạt loại giỏi, biết rằng cán bộ đó là nữ (làm tròn kết quả đến hàng phần trăm).

Trong 10000 áo sơ mi xuất khẩu của một doanh nghiệp dệt may có 1000 áo sơ mi trắng. Các áo sơ mi trắng đó gồm ba cỡ: 40,41,42, trong đó có 200 áo cỡ 40 . Chọn ra ngẫu nhiên một chiếc áo trong 10000 áo sơ mi xuất khẩu. Giả sử chiếc áo sơ mi được chọn ra là áo sơ mi trắng. Tính xác suất để chiếc áo sơ mi đó có cỡ 40 .

Một hộp đựng 5 quả bóng màu vàng và 3 quả bóng màu trắng, các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên lần thứ nhất một quả bóng (không hoàn lại), rồi lần thứ hai lấy một quả bóng khác. Tính xác suất để lần thứ nhất lấy được quả bóng màu vàng, lần thứ hai lấy được quả bóng màu trắng.

Một hộp có 6 quả bóng màu xanh, 4 quả bóng màu đỏ; các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên lần lượt hai quả bóng trong hộp, lấy không hoàn lại. Tìm xác suất để lần thứ hai lấy được quả bóng màu đỏ, biết rằng lần thứ nhất đã lấy được quả bóng màu xanh.

Một hộp đựng 24 chai nước giải khát có hình dạng và kích thước như nhau, trong đó có 2 chai nước giải khát ghi giải thường "Bạn nhận được thêm một chai nước giải khát". Chọn ra ngẫu nhiên lần lượt (không hoàn lại) hai chai nước trong hộp. Tính xác suất để cả hai chai đều ghi giải thưởng.

Một công ty có hai chi nhánh. Sản phẩm của chi nhánh I chiếm \(54\% \) tổng sản phẩm của công ty. Trong quá trình sản xuất phân loại, có \(75\% \) sản phẩm của công ty đạt loại A , trong đó có \(65\% \) của chi nhánh I. Chọn ngẫu nhiên một sản phẩm của công ty. Tính xác suất sản phẩm được chọn đạt loại A , biết rằng sản phẩm được chọn của chi nhánh I (làm tròn kết quả đến hàng phần mười).

Một hộp có 3 quả bóng màu xanh, 4 quả bóng màu đỏ; các quả bóng có kích thước và khối lượng như nhau. Lấy bóng ngẫu nhiên hai lần liên tiếp, trong đó mỗi lần lấy ngẫu nhiên một quả bóng trong hộp, ghi lại màu của quả bóng lấy ra và bỏ lại quả bóng đó vào hộp. Xét các biến cố:

A: "Quả bóng màu xanh được lấy ra ở lần thứ nhất";

\(B\) : "Quả bóng màu đỏ được lấy ra ở lần thứ hai".

Chứng minh rằng \(A\), \(B\) là hai biến cố độc lập.