15 bài tập Tính xác suất có điều kiện bằng sơ đồ hình cây (có lời giải)
20 câu hỏi
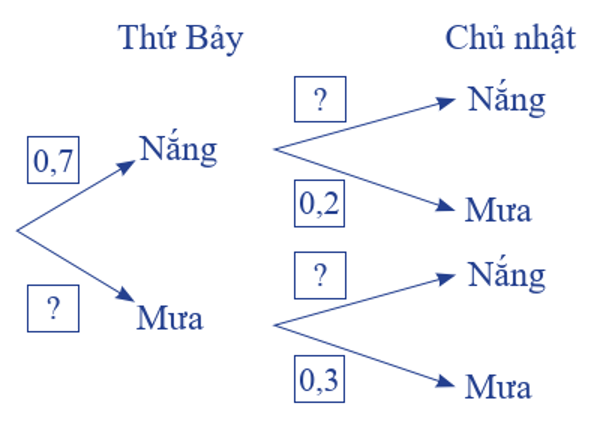
Bạn Việt chuẩn bị đi tham quan một hòn đảo trong hai ngày thứ Bảy và Chủ nhật. Ở hòn đảo đó, mỗi ngày chỉ có nắng hoặc mưa, nếu một ngày là nắng thì khả năng xảy ra mưa ở ngày tiếp theo là \(20\% \), còn nếu một ngày là mưa thì khả năng ngày hôm sau vẫn mưa là \(30\% \). Theo dự báo thời tiết, xác suất trời sẽ nắng vào thứ Bảy là 0,7 .
Hãy tìm các giá trị thích hợp thay vào ô có dấu ? ở sơ đồ hình cây sau:
Ở một sân bay, người ta sử dụng một loại máy soi tự động phát hiện hàng cấm trong hành lí kí gửi. Máy phát chuông cảnh báo với \(95\% \) các kiện hành lí có chứa hàng cấm và \(2\% \) các kiện hành lí không chứa hàng cấm. Tỉ lệ các kiện hành lí có chứa hàng cấm là \(0,1\% \).
Chọn ngẫu nhiên một kiện hành lí để soi bằng máy trên. Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:
M: "Kiện hành lí có chứa hàng cấm và máy phát chuông cảnh báo";
\(N\) : "Kiện hành lí không chứa hàng cấm và máy phát chuông cảnh báo".
Hộp thứ nhất có 4 viên bi xanh và 6 viên bi đỏ. Hộp thứ hai có 5 viên bi xanh và 4 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên 1 viên bi từ hộp thứ hai.
Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:
A: "Viên bi lấy ra từ hộp thứ nhất có màu xanh và viên bi lấy ra từ hộp thứ hai có màu đỏ";
B: "Hai viên bi lấy ra có cùng màu".
Một trường đại học tiến hành khảo sát tình trạng việc làm sau khi tốt nghiệp của sinh viên. Kết quả khảo sát cho thấy tỉ lệ người tìm được việc làm đúng chuyên ngành là \(85\% \) đối với sinh viên tốt nghiệp loại giỏi và \(70\% \) đối với sinh viên tốt nghiệp loại khác.
Tỉ lệ sinh viên tốt nghiệp loại giỏi là \(30\% \). Gặp ngẫu nhiên một sinh viên đã tốt nghiệp của trường.
Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:
C: "Sinh viên tốt nghiệp loại giỏi và tìm được việc làm đúng chuyên ngành";
\(D\) : "Sinh viên không tốt nghiệp loại giỏi và tìm được việc làm đúng chuyên ngành".
Mỗi bạn học sinh trong lớp của Minh lựa chọn học một trong hai ngoại ngữ là tiếng Anh hoặc tiếng Nhật. Xác suất chọn tiếng Anh của mỗi bạn học sinh nữ là 0,6 và của mỗi bạn học sinh nam là 0,7 . Lớp của Minh có 25 bạn nữ và 20 bạn nam. Chọn ra ngẫu nhiên một bạn trong lớp.
Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:
\(A\): "Bạn được chọn là nam và học tiếng Nhật";
\(B\) : "Bạn được chọn là nữ và học tiếng Anh".
Máy tính và thiết bị lưu điện (UPS) được kết nối như Hình vẽ. Khi xảy ra sự cố điện, UPS bị hỏng với xác suất 0,02 . Nếu UPS bị hỏng khi xảy ra sự cố điện, máy tính sẽ bị hòng với xác suất 0,1 ; ngược lại, nếu UPS không bị hòng, máy tính sẽ không bị hỏng.

Tính xác suất để cả UPS và máy tính đều không bị hỏng khi xảy ra sự cố điện.
Máy tính và thiết bị lưu điện (UPS) được kết nối như Hình vẽ. Khi xảy ra sự cố điện, UPS bị hỏng với xác suất 0,02 . Nếu UPS bị hỏng khi xảy ra sự cố điện, máy tính sẽ bị hòng với xác suất 0,1 ; ngược lại, nếu UPS không bị hòng, máy tính sẽ không bị hỏng.

Tính xác suất để cả UPS và máy tính đều bị hỏng khi xảy ra sự cố điện.
Trong một hộp kín có 7 chiếc bút bi xanh và 5 chiếc bút bi đen, các chiếc bút có cùng kích thước và khối lượng. Bạn Sơn lấy ngẫu nhiên một chiếc bút bi từ trong hộp, không trả lại. Sau đó bạn Tùng lấy ngẫu nhiên một trong 11 chiếc bút còn lại.
Tính xác suất để Sơn lấy được bút bi đen và Tùng lấy được bút bi xanh.
Trong một hộp kín có 7 chiếc bút bi xanh và 5 chiếc bút bi đen, các chiếc bút có cùng kích thước và khối lượng. Bạn Sơn lấy ngẫu nhiên một chiếc bút bi từ trong hộp, không trả lại. Sau đó bạn Tùng lấy ngẫu nhiên một trong 11 chiếc bút còn lại.
Tính xác suất Sơn lấy được bút bi xanh và Tùng lấy được bút bi đen;
Trong một hộp kín có 7 chiếc bút bi xanh và 5 chiếc bút bi đen, các chiếc bút có cùng kích thước và khối lượng. Bạn Sơn lấy ngẫu nhiên một chiếc bút bi từ trong hộp, không trả lại. Sau đó bạn Tùng lấy ngẫu nhiên một trong 11 chiếc bút còn lại.
Tính xác suất để hai chiếc bút lấy ra có cùng màu.
Một hộp có 8 viên bi màu đỏ và 5 viên bi màu vàng; các viên bi có kích thước và khối lượng như nhau. Có 5 viên bi trong hộp được đánh số, trong đó có 3 viên bi màu đỏ và 2 viên bi màu vàng. Lấy ngẫu nhiên một viên bi trong hộp. Dùng sơ đồ hình cây, tính xác suất để viên bi được lấy ra có màu đỏ, biết rằng viên bi đó được đánh số.
Một hộp có 12 quả bóng bàn màu trắng và 10 quả bóng bàn màu vàng; các quả bóng có kích thước và khối lượng như nhau. Có 10 quả bóng bàn trong hộp được đánh số, trong đó có 4 quả bóng bàn màu trắng và 6 quả bóng bàn màu vàng. Lấy ngẫu nhiên một quả bóng bàn trong hộp. Dùng sơ đồ hình cây, tính xác suất để quả bóng bàn được lấy ra có màu trắng, biết rằng quả bóng bàn đó được đánh số.
Một hộp có 12 quả bóng màu xanh, 7 quả bóng màu đỏ; các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên lần lượt hai quả bóng trong hộp, lấy không hoàn lại. Dùng sơ đồ hình cây, tính xác suất để lần thứ hai lấy được quả bóng màu đỏ, biết rằng lần thứ nhất đã lấy được quả bóng màu xanh.
Một túi có 10 hộp sữa chua dâu và 10 hộp sửa chua nha đam; các hộp sữa chua có kích thươ̂c và khối lượng như nhau. Có 12 hộp sữa chua trong túi là sữa chua không đường, trong đó có 6 hộp sữa chua dâu và 6 hộp sữa chua nha đam. Lấy ngẫu nhiên một hộp sữa chua trong túi. Dùng sơ đồ hình cây, tính xác suất để hộp sữa chua được lấy ra là hộp sữa chua dâu, biết rằng hộp sữa chua đó là sữa chua không đường.
Trên giá sách có 10 quyển sách Khoa học và 15 quyển sách Nghệ thuật. Có 9 quyển sách viết bằng tiếng Anh, trong đó 3 quyển sách Khoa học và 6 quyển sách Nghệ thuật, các quyển sách còn lại viết bằng tiếng Việt. Lấy ngẫu nhiên một quyển sách. Dùng sơ đồ hình cây, tính xác suất để quyển sách được lấy ra là sách viết bằng tiếng Việt, biết rằng quyển sách đó là sách Khoa học.
Ô cửa bí mật (Let's Make a Deal) là một trò chơi trên truyền hình nổi tiếng ở Mỹ, đã được mua bản quyền và phát sóng ở nhiều nước trên thế giới. Nội dung trò chơi như sau:
- Người chơi được mời lên sân khấu và đứng trước ba cánh cửa đóng kín. Sau một cánh cửa có chiếc ô tô, sau mỗi cánh cửa còn lại là một con lừa. Người chơi được yêu cầu chọn ngẫu nhiên một cánh cửa, nhưng không được mở ra.
- Tiếp đó người quản trò tuyên bố sẽ mở ngẫu nhiên một trong hai cánh cửa người chơi không chọn mà sau cửa đó là con lừa. Người quản trò hỏi người chơi muốn giữ nguyên sự lựa chọn ban đầu của mình hay muốn chuyển sang cửa chưa mở còn lại.
Giả sử người chơi chọn cửa số 1 và người quản trò mở cửa số 3 .
Kí hiệu \({E_1};{E_2}\); \({E_3}\) tương ứng là các biến cố: "Sau ô cửa số 1 có ô tô"; "Sau ô cửa số 2 có ô tô"; "Sau ô cửa số 3 có ô tô" và \(H\) là biến cố: "Người quản trò mở ô cửa số 3 thấy con lừa".
Sau khi người quản trò mở cánh cửa số 3 thấy con lừa, tức là khi \(H\) xảy ra. Để quyết định thay đổi lựa chọn hay không, người chơi cần so sánh hai xác suất có điều kiện: \(P\left( {{E_1}\mid H} \right)\) và \(P\left( {{E_2}\mid H} \right)\).
Chứng minh rằng:
- \(P\left( {{E_1}} \right) = P\left( {{E_2}} \right) = P\left( {{E_3}} \right) = \frac{1}{3}\);
- \(P\left( {H\mid {E_1}} \right) = \frac{1}{2}\) và \(P\left( {H\mid {E_2}} \right) = 1\).
Ô cửa bí mật (Let's Make a Deal) là một trò chơi trên truyền hình nổi tiếng ở Mỹ, đã được mua bản quyền và phát sóng ở nhiều nước trên thế giới. Nội dung trò chơi như sau:
- Người chơi được mời lên sân khấu và đứng trước ba cánh cửa đóng kín. Sau một cánh cửa có chiếc ô tô, sau mỗi cánh cửa còn lại là một con lừa. Người chơi được yêu cầu chọn ngẫu nhiên một cánh cửa, nhưng không được mở ra.
- Tiếp đó người quản trò tuyên bố sẽ mở ngẫu nhiên một trong hai cánh cửa người chơi không chọn mà sau cửa đó là con lừa. Người quản trò hỏi người chơi muốn giữ nguyên sự lựa chọn ban đầu của mình hay muốn chuyển sang cửa chưa mở còn lại.
Giả sử người chơi chọn cửa số 1 và người quản trò mở cửa số 3 .
Kí hiệu \({E_1};{E_2}\); \({E_3}\) tương ứng là các biến cố: "Sau ô cửa số 1 có ô tô"; "Sau ô cửa số 2 có ô tô"; "Sau ô cửa số 3 có ô tô" và \(H\) là biến cố: "Người quản trò mở ô cửa số 3 thấy con lừa".
Sau khi người quản trò mở cánh cửa số 3 thấy con lừa, tức là khi \(H\) xảy ra. Để quyết định thay đổi lựa chọn hay không, người chơi cần so sánh hai xác suất có điều kiện: \(P\left( {{E_1}\mid H} \right)\) và \(P\left( {{E_2}\mid H} \right)\).
Sử dụng công thức tính xác suất có điều kiện và công thức nhân xác suất, chứng minh rằng:
- \(P\left( {{E_1}\mid H} \right) = \frac{{P\left( {{E_1}} \right) \cdot P\left( {H\mid {E_1}} \right)}}{{P(H)}}\);
- \(P\left( {{E_2}\mid H} \right) = \frac{{P\left( {{E_2}} \right) \cdot P\left( {H\mid {E_2}} \right)}}{{P(H)}}\).
Ô cửa bí mật (Let's Make a Deal) là một trò chơi trên truyền hình nổi tiếng ở Mỹ, đã được mua bản quyền và phát sóng ở nhiều nước trên thế giới. Nội dung trò chơi như sau:
- Người chơi được mời lên sân khấu và đứng trước ba cánh cửa đóng kín. Sau một cánh cửa có chiếc ô tô, sau mỗi cánh cửa còn lại là một con lừa. Người chơi được yêu cầu chọn ngẫu nhiên một cánh cửa, nhưng không được mở ra.
- Tiếp đó người quản trò tuyên bố sẽ mở ngẫu nhiên một trong hai cánh cửa người chơi không chọn mà sau cửa đó là con lừa. Người quản trò hỏi người chơi muốn giữ nguyên sự lựa chọn ban đầu của mình hay muốn chuyển sang cửa chưa mở còn lại.
Giả sử người chơi chọn cửa số 1 và người quản trò mở cửa số 3 .
Kí hiệu \({E_1};{E_2}\); \({E_3}\) tương ứng là các biến cố: "Sau ô cửa số 1 có ô tô"; "Sau ô cửa số 2 có ô tô"; "Sau ô cửa số 3 có ô tô" và \(H\) là biến cố: "Người quản trò mở ô cửa số 3 thấy con lừa".
Sau khi người quản trò mở cánh cửa số 3 thấy con lừa, tức là khi \(H\) xảy ra. Để quyết định thay đổi lựa chọn hay không, người chơi cần so sánh hai xác suất có điều kiện: \(P\left( {{E_1}\mid H} \right)\) và \(P\left( {{E_2}\mid H} \right)\).
Từ các kết quả trên hãy suy ra:
\(P\left( {{E_2}\mid H} \right) = 2P\left( {{E_1}\mid H} \right).\)
Từ đó hãy đưa ra lời khuyên cho người chơi: Nên giữ nguyên sự lựa chọn ban đầu hay chuyển sang cửa chưa mở còn lại?
Hướng dẫn: Nếu \({E_1}\) xảy ra, tức là sau cửa số 1 có ô tô. Khi đó, sau cửa số 2 và 3 là con lừa. Người quản trò chọn ngẫu nhiên một trong hai cửa số 2 và 3 để mở ra. Do đó, việc chọn cửa số 2 hay cửa số 3 có khả năng như nhau. Vậy \(P\left( {H\mid {E_1}} \right) = \frac{1}{2}\).
Nếu \({E_2}\) xảy ra, tức là cửa số 2 có ô tô. Khi đó, người quản trò chắc chắn phải mở cửa số 3 . Do đó \(P\left( {H\mid {E_2}} \right) = 1\).
Người chơi nên chuyển sang cửa số 2 . Bởi vì với điều kiện H "người quản trò mở cửa số 3 ở đó không có ô tô" thì xác suất để cửa số 2 có ô tô gấp đôi xác suất để cửa số 1 có ô tô.
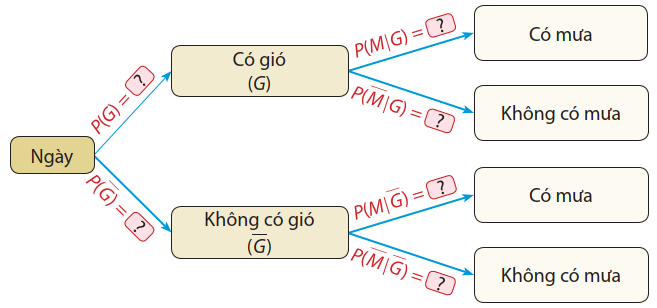
Theo kết quả từ trạm nghiên cứu khí hậu tại địa phương T , xác suất để một ngày có gió là 0,6 ; nếu ngày có gió thì xác suất có mưa là 0,4 ; nếu ngày không có gió thì xác suất có mưa là 0,2 . Gọi \(G\) là biến cố "Ngày có gió" và \(M\) là biến cố "Ngày có mưa".
Vẽ lại sơ đồ hình cây sau và điền vào ô có dấu ? các giá trị xác suất tương ứng:
Người chơi nên chuyển sang cửa số 2 . Bởi vì với điều kiện H "người quản trò mở cửa số 3 ở đó không có ô tô" thì xác suất để cửa số 2 có ô tô gấp đôi xác suất để cửa số 1 có ô tô.
Theo kết quả từ trạm nghiên cứu khí hậu tại địa phương T , xác suất để một ngày có gió là 0,6 ; nếu ngày có gió thì xác suất có mưa là 0,4 ; nếu ngày không có gió thì xác suất có mưa là 0,2 . Gọi \(G\) là biến cố "Ngày có gió" và \(M\) là biến cố "Ngày có mưa".
Tính xác suất \(P(GM)\) và \(P(G\bar M)\). Nêu ý nghĩa của các xác suất này.








