30 câu hỏi
Một tập hợp 100 phần tử có bao nhiêu tập con có 2 phần tử?
298
4950
50
9900
Có 20 vé số khác nhau trong đó có 3 vé chứa các giải Nhất, Nhì, Ba. Hỏi có bao nhiêu cách trao giải thưởng cho 20 người, mỗi người giữ một vé?
1140
8000
2280
6840
Một tổ bộ môn có 10 nam và 15 nữ. Có bao nhiêu cách chọn một hội đồng gồm 6 ủy viên, trong đó số ủy viên nam gấp đôi số ủy viên nữ?
22050
315
54600
575
Công thức nào sau đây đúng. Cho n là số nguyên dương, khi đó 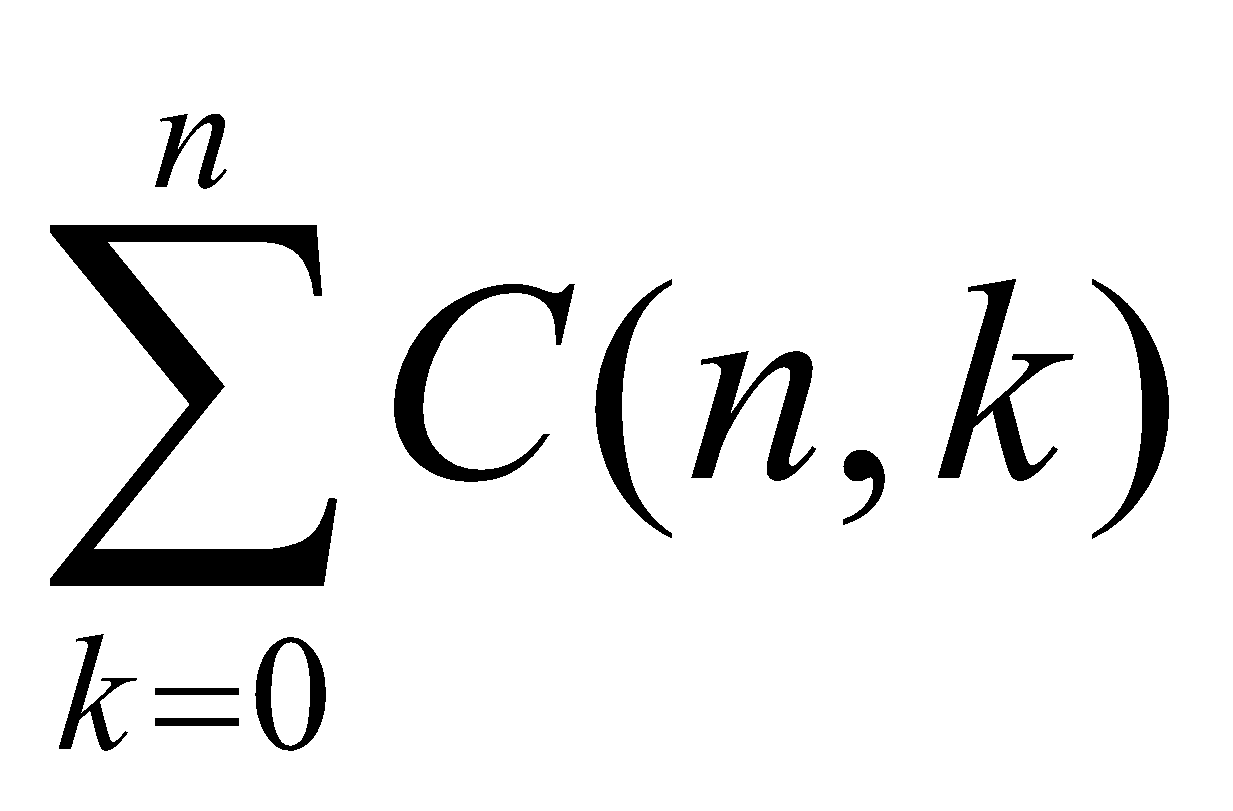 là.
là.
2n-1
2n
2n+1
2n -1
Công thức nào sau đây đúng. Cho n và k là các số nguyên dương với n ≥ k. Khi đó.
C(n+1, k) = C(n, k−1) + C(n, k)
C(n+1, k) = C(n−1, k) + C(n−1, k−1)
C(n+1, k) = C(n, k) + C(n−1, k)
C(n+1, k) = C(n−1, k−1) + C(n, k−1)
Công thức nào sau đây đúng. Cho x, y là 2 biến và n là một số nguyên dương. Khi đó.
A. 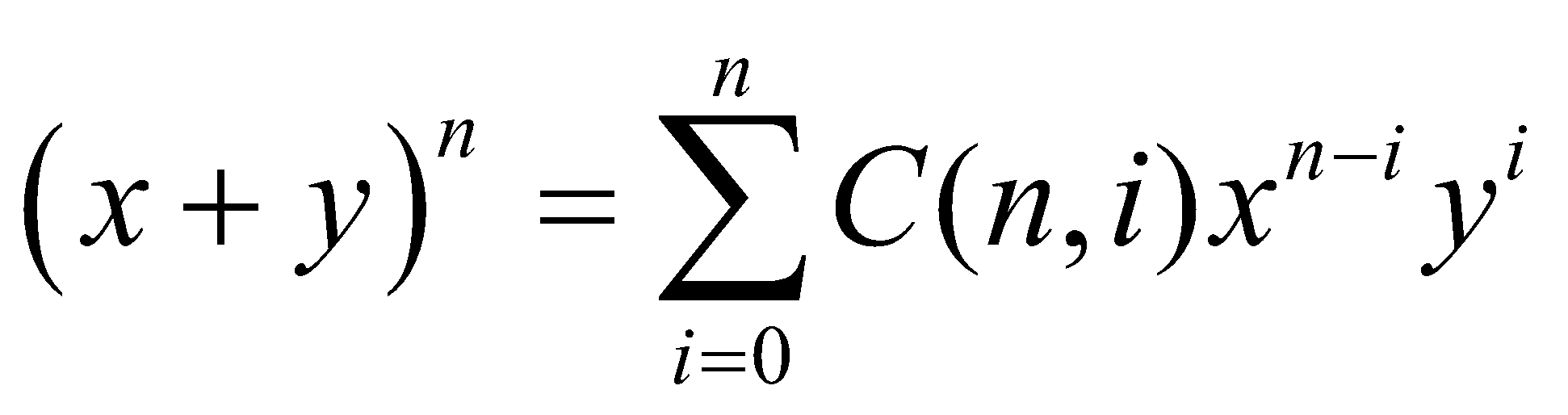
B. 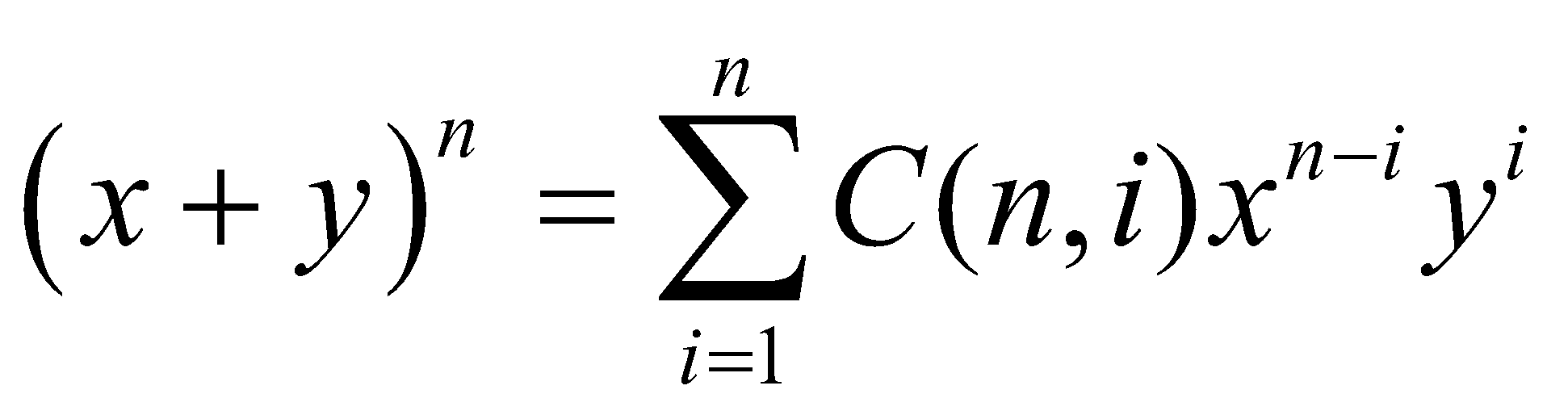
C. 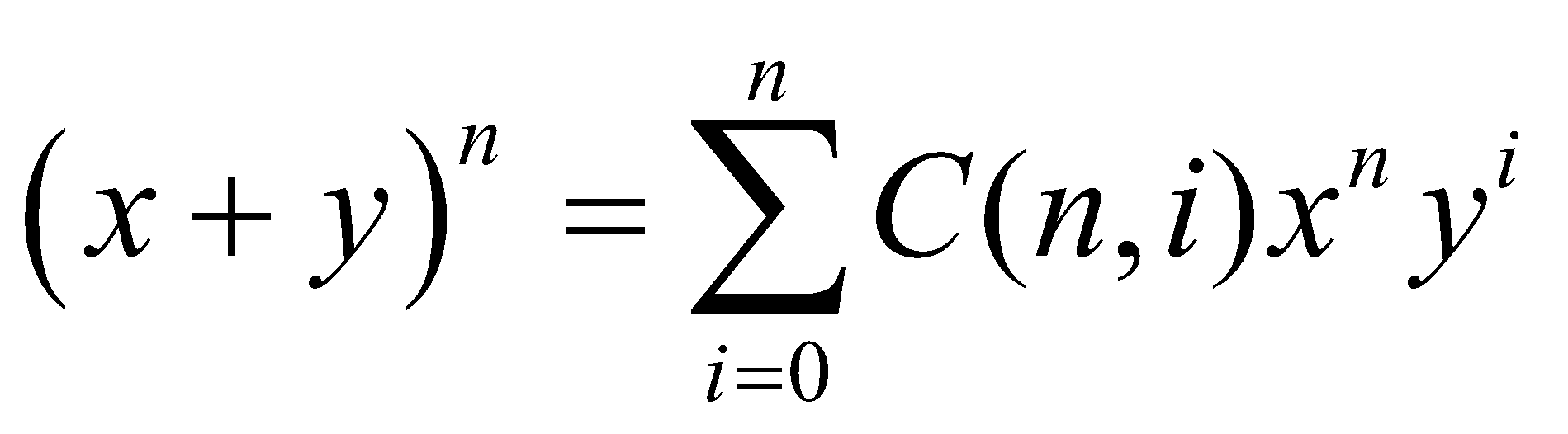
D. ![]()
Hệ số của x12y13 trong khai triển (x+y)25 là.
25!
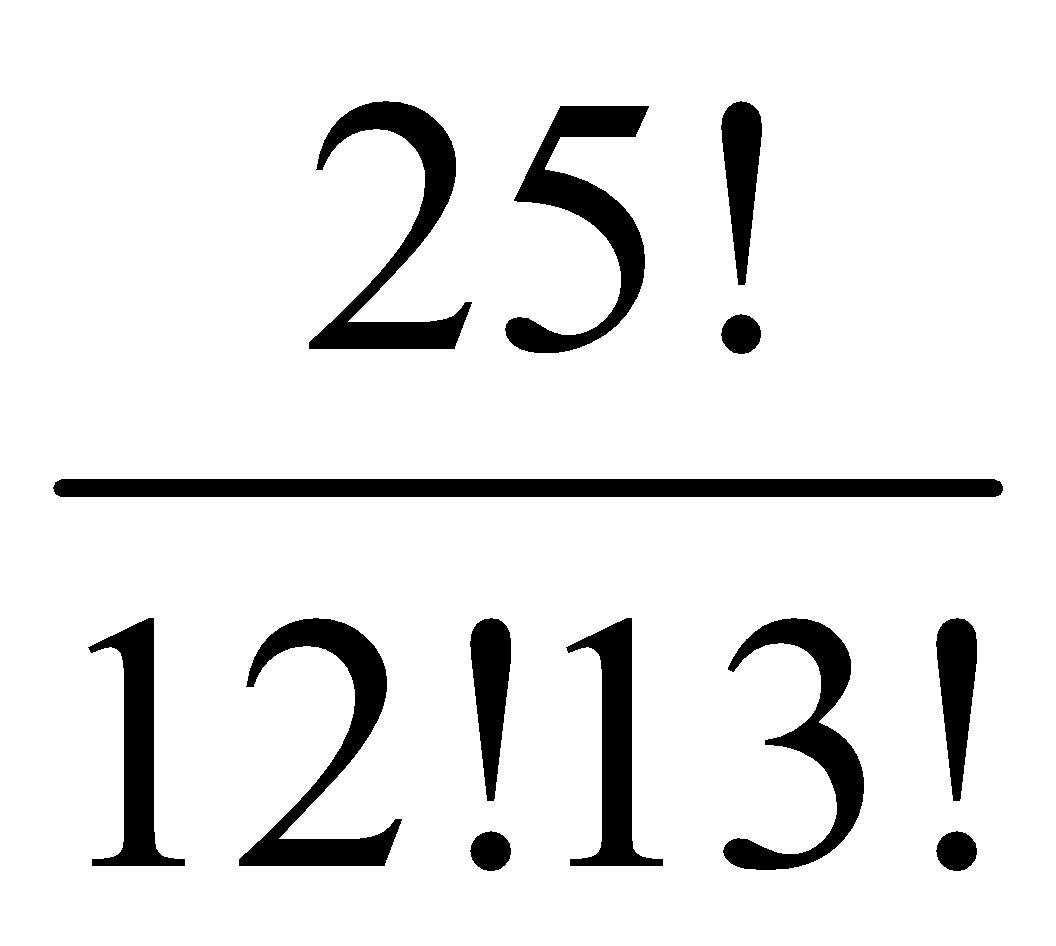
![]()
![]()
Cho n, r là các số nguyên không âm sao cho r ≤ n. Khi đó.
C(n, r) = C(n+r-1, r)
C(n, r) = C(n, r-1)
C(n, r) = C(n, n-r)
C(n, r) = C(n-r, r)
Trong khai triển (x+y)200 có bao nhiêu số hạng?
100
101
200
201
Tìm hệ số của x9 trong khai triển của (2 - x)20
C(20,10).210
(20,9).211
– C(20,9)211
– C(20,10)29
Có bao nhiêu cách tuyển 5 trong số 10 cầu thủ của một đội quần vợt để đi thi đấu tại một trường khác?
252
250
120
30240
Có bao nhiêu khả năng có thể xảy ra đối với các vị trí thứ nhất, thứ nhì và thứ ba trong cuộc đua có 12 con ngựa, nếu mọi thứ tự tới đích đều có thể xảy ra?
220
1320
123
312
Có bao nhiêu số tự nhiên có 3 chữ số khác nhau được tạo từ tập các chữ số {1,3,5,7,9}.
30
60
90
120
Có bao nhiêu số tự nhiên có 3 chữ số được tạo từ tập các chữ số {1,3,5,7,9}.
125
60
65
120
Có bao nhiêu số lẻ có 3 chữ số được tạo từ tập các chữ số {0,1,2,3,4,5}.
48
60
90
75
Trong một khoa có 20 sinh viên xuất sắc về Toán và 12 sinh viên xuất sắc về CNTT. Hỏi có bao nhiêu cách lựa chọn hai đại diện sao cho một là sinh viên Toán, một là sinh viên CNTT?
20
12
32
240
Có bao nhiêu xâu nhị phân có độ dài bằng 5 mà hoặc có 2 bít đầu tiên là 0 hoặc có 2 bít cuối cùng là 1?
16
14
2
32
Mỗi thành viên trong câu lạc bộ Toán tin có quê ở 1 trong 20 tỉnh thành. Hỏi cần phải tuyển bao nhiêu thành viên để đảm bảo có ít nhất 5 người cùng quê?
81
99
101
90
Có bao nhiêu hàm số khác nhau từ tập có 4 phần tử đến tập có 3 phần tử. A. 81
64
4
12
Số xâu nhị phân độ dài 4 có bít cuối cùng bằng 1 là.
8
12
16
A, B và C đều sai
Một quan hệ hai ngôi R trên một tập hợp X (khác rỗng) được gọi là quan hệ tương đương nếu và chỉ nếu nó có 3 tính chất sau.
Phản xạ – Đối xứng – Bắc cầu
Phản xạ – Phản đối xứng – Bắc cầu
Đối xứng – Phản đối xứng – Bắc cầu
Phản xạ – Đối xứng – Phản đối xứng.
Một quan hệ hai ngôi R trên một tập hợp X (khác rỗng) được gọi là quan hệ thứ tự nếu và chỉ nếu nó có 3 tính chất sau.
Phản xạ – Đối xứng – Bắc cầu
Phản xạ – Phản đối xứng – Bắc cầu
Đối xứng – Phản đối xứng – Bắc cầu
Phản xạ – Đối xứng – Phản đối xứng.
Cho biết quan hệ nào là quan hệ tương đương trên tập {0, 1, 2, 3}.
{(0,0),(1,1),(2,2),(3,3),(0,1),(0,2),(0,3)}
{(0,0),(1,1),(2,2),(3,3),(0,1),(1,0)}
{(0,0),(0,2),(2,0),(2,2),(2,3),(3,2),(3,3)}
{(0,0),(1,1),(1,3),(2,2),(2,3),(3,1),(3,2),(3,3)}
Cho A ={1, 2, 3, 4, 5}. Quan hệ R được xác định: ∀a,b ∈ A, aRb ⇔ a + b = 2k (k=1,2,...) Quan hệ R được biểu diễn là.
{(1,1),(2,2),(3,3),(4,4), (1,3),(3,1),(1,5),(5,1), (2,4),(4,2)}
{(1,1),(2,2),(3,3),(4,4),(5,5),(1,3),(1,5), (3,5), (2,4)}
{(1,1),(2,2),(3,3),(4,4),(5,5),(1,3),(3,1),(1,5),(5,1), (3,5), (5,3),(2,4),(4,2)}
{(1,3),(3,1),(1,5),(5,1), (3,5), (5,3),(2,4),(4,2)}
Xác định quan hệ tương đương được biểu diễn bởi các ma trận logic dưới đây.
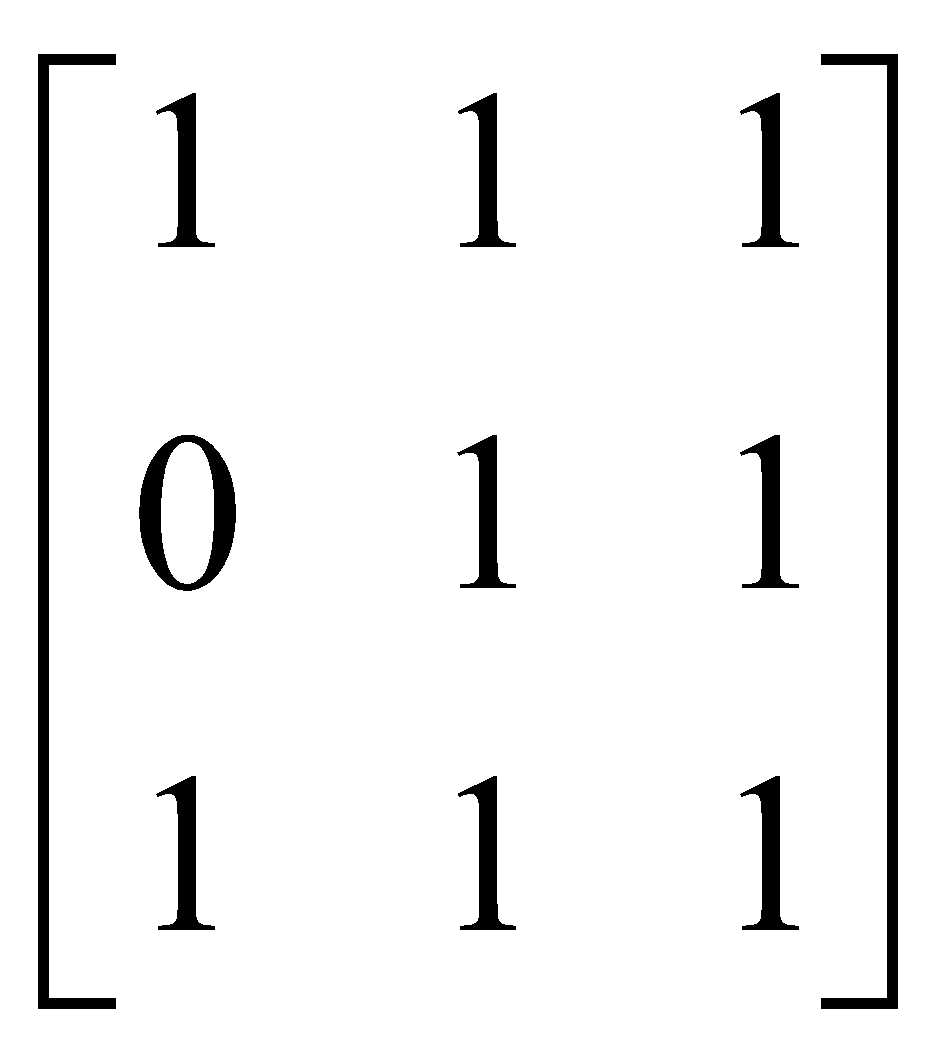

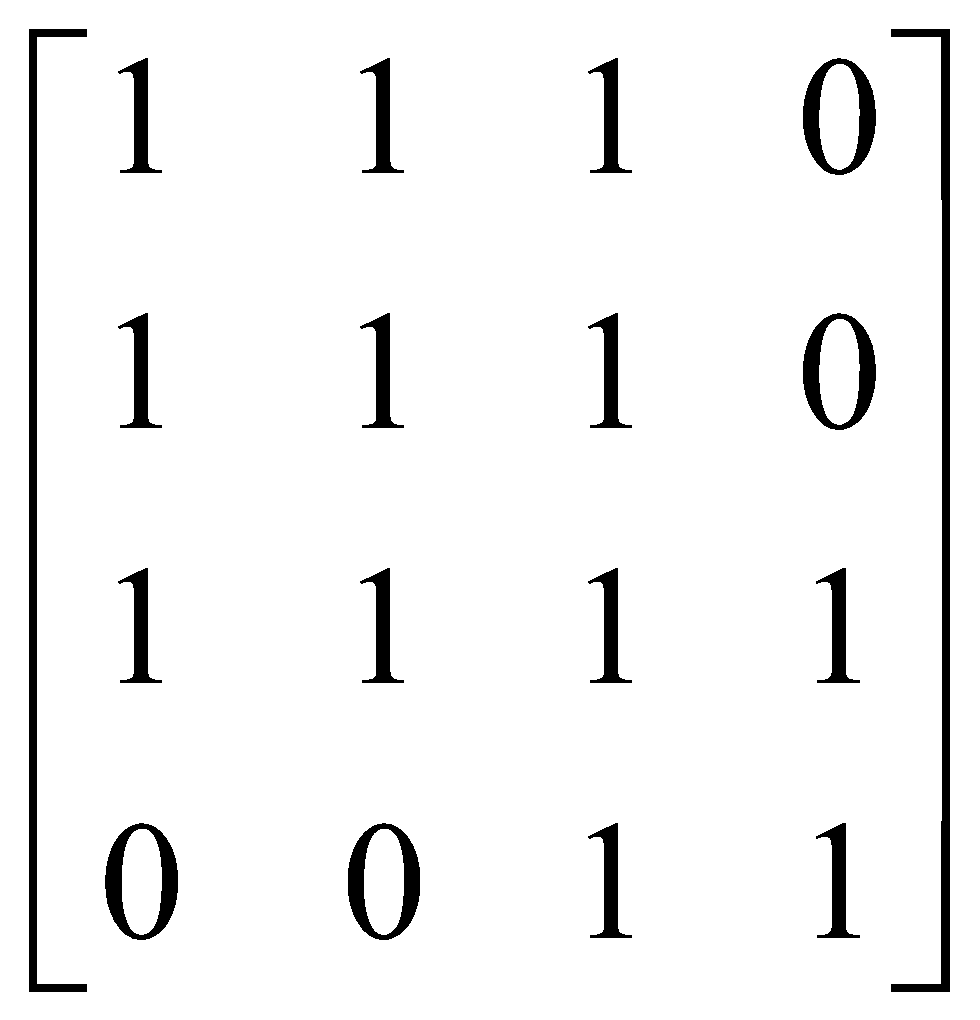
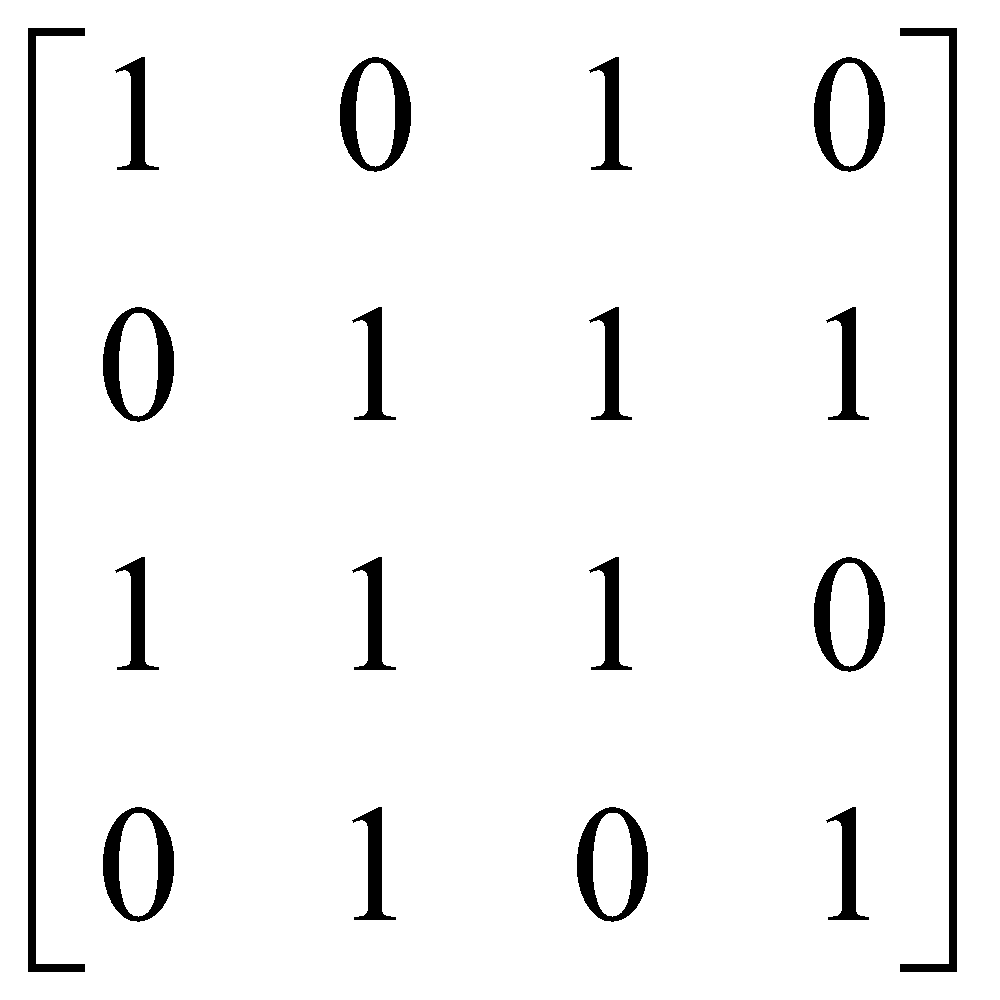
Cho A = {1,2,3,4,5}. Trên A xác định quan hệ R như sau: ∀a,b ∈ A, aRb ⇔ a + b = 2k+1 (k=1,2,...) Quan hệ R được biểu diễn là.
{(1,2),(1,4),(2,3),(2,5)}
{(1,1),(2,2),(3,3),(4,4),(5,5), (1,2),(1,4),(2,3),(2,5)}
{(1,2),(2,1),(1,4),(4,1), (2,5), (5,2)}
{(1,2),(2,1),(1,4),(4,1), (2,5), (5,2),(3,4),(4,3),(2,3),(3,2),(4,5),(5,4)}
Cho tập A = {1,2,3,4,5}. Cho A1 = {1}, A2 = {2,3}, A3 = {4,5}. Quan hệ tương đương R trên A sinh ra phân hoạch A1, A2, A3 là.
{(1,1),(2,3),(4,5),(2,2),(3,3), (3,2),(4,4),(5,5),(5,4)}
{(1,1),(2,2),(3,3),(4,4),(5,5), (1,2),(1,3),(1,4),(1,5)}
{(1,1),(2,3),(3,2),(4,5), (5,4)}
{(2,2),(2,3),(3,2),(3,3), (4,4), (4,5),(5,4),(5,5), (1,1),(1,2),(2,1),(1,3),(3,1)}
Cho tập A = {1,2,3,4,5,6}. Cho A1 = {1,2}, A2 = {3,4}, A3 = {5,6}. Quan hệ tương đương R trên A sinh ra phân hoạch A1, A2, A3 là.
{(1,1),(2,3),(4,5),(2,2),(3,3), (3,2),(4,4),(5,5),(5,4),(6,6),(5,6),(6,5)}
{(1,1),(2,2),(3,3),(4,4),(5,5), (6,6),(1,2),(2,1),(3,4),(4,3),(5,6),(6,5)}
{(1,1),(1,2),(2,2),(3,4), (3,3),(5,6),(4,4),(5,5),(6,6)}
{(2,2),(2,3),(1,1),(3,3), (4,4), (3,4),(4,3),(2,1), (1,1),(1,2),(2,1),(5,6),(6,5)}
Cho tập A = {1,2,3,4,5} và quan hệ tương đương R trên A như sau: R = {(1,1),(2,2),(3,3),(4,4),(5,5),(2,4),(4,2)}. Xác định phân hoạch do R sinh ra.
A1 = {1,3,5}, A2 = {2,4}
A1 = {1}, A2 = {2,4}, A3 = {3,5}
A1 = {1}, A2 = {2,4}, A3 = {3}, A4 = {5}
A1 = {1,2}, A2 = {3,4}, A3 = {5}
Cho A ={1, 2, 3, 4, 5}. Quan hệ R được xác định: ∀a, b ∈ A, aRb ⇔ a + b = 2k (k=1,2,...). Xác định phân hoạch do R sinh ra.
A1 = {1,3}, A2 = {2,4}, A3 = {5}
A1 = {1}, A2 = {2,4}, A3 = {3}, A4 = {5}
A1 = {1}, A2 = {2}, A3 = {3}, A4 = {4}, A5 = {5}
A1 = {1,3,5}, A2 = {2,4}
