36 CÂU HỎI
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Góc giữa hai đường thẳng SB và AD bằng góc giữa hai đường thẳng
A. SB và AC.
B. SB và BC.
C. SA và AD.
D. SC và AD.
Trong không gian cho mặt phẳng (P) và điểm M. Có tất cả bao nhiêu đường thẳng đi qua M và vuông góc với mặt phẳng (P)?
A. 0.
B. 1.
C. 2.
D. Vô số.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(SA \bot \left( {ABCD} \right)\).Mệnh đề nào sau đây đúng?
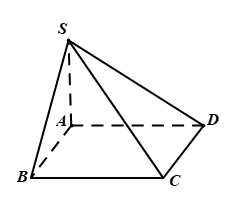
A.\(d\left( {D,\left( {SAB} \right)} \right) = SD\).
B. \(d\left( {D,\left( {SAB} \right)} \right) = DC\).
C.\(d\left( {D,\left( {SAB} \right)} \right) = AD\).
D. \(d\left( {D,\left( {SAB} \right)} \right) = DB\).
Cho ba đường thẳng \(a\), \(b\) và \(c\) thỏa mãn \(a\,{\rm{//}}\,b\). Chọn mệnh đề sai trong các mệnh đề dưới đây?
A. Góc giữa hai đường thẳng \(b\) và \(c\) là chính góc giữa hai đường thẳng \(c\) và \(a\).
B. Góc giữa hai đường thẳng \(a\) và \(c\) là chính góc giữa hai đường thẳng \(b\) và \(c\).
C. Góc giữa hai đường thẳng \(a\) và \(b\) bằng \(0^\circ \).
D. Góc giữa hai đường thẳng \(a\) và \(c\) là chính góc giữa hai đường thẳng \(a\) và \(b\).
Cho hình lăng trụ \(ABC.A'B'C'\) như hình vẽ bên. Góc giữa hai đường thẳng \(AA'\) và \(BC\) là góc
A. \(\left( {AA',AB} \right)\).
B. \(\left( {CC',AC} \right)\).
C. \(\left( {BB',BC} \right)\).
D. \(\left( {BB',AB} \right)\).
Cho hình lăng trụ \(ABCD.A'B'C'D'\) như hình vẽ. Góc giữa hai đường thẳng \(BB'\) và \(AC\) là góc nào dưới đây?
A. \(\left( {CC',AC} \right)\).
B. \(\left( {CC',CD} \right)\).
C. \(\left( {AA',AD} \right)\).
D. \(\left( {AB,AC} \right)\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, tam giác \(SAB\) vuông tại \(A\). Góc giữa hai đường thẳng \(SA\) và \(CD\) bằng bao nhiêu?
A. \(45^\circ \).
B. \(30^\circ \).
C. \(60^\circ \).
D. \(90^\circ \).
Cho hình chóp \(S.ABC\) có \[SA \bot \left( {ABC} \right)\] và \(AB \bot BC.\) Số các mặt của hình chóp \(S.ABC\) là tam giác vuông là
A. \(1.\)
B. \(3.\)
C. \(2.\)
D. \(4.\)
Cho hình chóp \(S.ABCD\)có đáy\(ABCD\) là hình vuông, \(SA\) vuông góc với mặt phẳng đáy. Khẳng định nào sau đây là đúng?
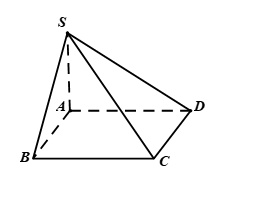
A. \(AB \bot \left( {SAD} \right)\).
B. \(AB \bot \left( {SAC} \right)\).
C. \(AB \bot \left( {SBC} \right)\).
D. \(AB \bot \left( {SCD} \right)\).
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\) và \(H\) là hình chiếu vuông góc của \(S\) lên \(BC\). Hãy chọn khẳng định đúng.
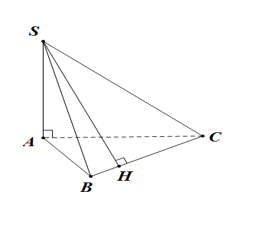
A. \(BC \bot SC\).
B. \(BC \bot AC\).
C. \(BC \bot AB\).
D. \(BC \bot AH\).
Cho tứ diện \(SABC\) có đáy \(ABC\) là tam giác vuông tại \(B\) và \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\). Gọi \(M\),\(N\)lần lượt là hình chiếu vuông góc của \(A\) trên cạnh \(SB\) và \(SC\). Khẳng định nào sau đây sai?
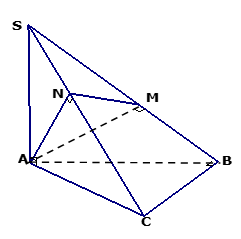
A. \[AM \bot SC\].
B. \[AM \bot MN\].
C. \[SA \bot BC\].
D. \[AN \bot SB\].
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật tâm \(O\), cạnh \(SA\) vuông góc với mặt phẳng đáy. Gọi \(H\) và \(K\) lần lượt là hình chiếu của \(A\) lên \(SB\) và \(SD\). Hỏi đường thẳng \(SC\) vuông góc với mặt phẳng nào trong các mặt phẳng sau đây?
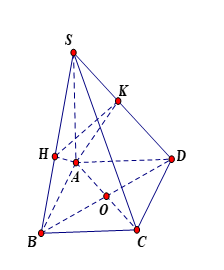
A. \(\left( {AHD} \right)\).
B. \(\left( {SBD} \right)\).
C. \(\left( {AKB} \right)\).
D. \(\left( {AHK} \right)\).
Cho hình chóp \(S.ABCD\)có \(SA \bot \left( {ABCD} \right)\), \(SA = 2\sqrt 6 \). Đáy \(ABCD\) là hình vuông cạnh bằng \(2\). Số đo góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng
A. \(30^\circ \).
B. \(60^\circ \).
C. \(45^\circ \).
D. \(75^\circ \).
Cho hình chóp \[S.ABCD\] có \(SA \bot \left( {ABCD} \right)\) và \(SA = a\), đáy \[ABCD\] là hình vuông cạnh bằng \[a\]. Góc giữa đường thẳng \[SC\] và mặt phẳng \[\left( {SAB} \right)\] bằng góc nào trong các góc dưới đây?
![Cho hình chóp \[S.ABCD\] có \(SA \bot \left( {ABCD} \right)\) và \(SA = a\), đáy \[ABCD\] là hình vuông cạnh bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid10-1736516466.png)
A. \(\widehat {BSC}\).
B. \(\widehat {SCB}\).
C. \(\widehat {SCA}\).
D. \(\widehat {ASC}\).
Cho hình chóp \[S.ABC\] có đáy \[ABC\] là tam giác vuông cân tại \[B\], \[SA \bot \left( {ABC} \right)\]. Tính số đo theo đơn vị độ của góc nhị diện \[\left[ {B,SA,C} \right]\].
![Cho hình chóp \[S.ABC\] có đáy \[ABC\] là tam giác vuông cân tại \[B\], \[SA \bot \left( {ABC} \right)\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid11-1736516551.png)
A. \(60^\circ \).
B. \(75^\circ \).
C. \(30^\circ \).
D. \(45^\circ \).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật có cạnh \(AB = a;BC = 2a\). Hai mặt bên \(SAB\) và \(SAD\) cùng vuông góc với mặt phẳng đáy \(ABCD\), cạnh \(SA = a\sqrt {15} \). Tính góc tạo bởi đường thẳng \(SC\) và mặt phẳng \(\left( {ABD} \right)\).
A. \(30^\circ \).
B. \(60^\circ \).
C. \(45^\circ \).
D. \(90^\circ \).
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông, hai đường thẳng \[AC\] và \[BD\] cắt nhau tại \[O\], \[SO \bot \left( {ABCD} \right)\], tam giác \[SAC\] là tam giác đều. Gọi \[M\] là trung điểm của cạnh \[AB\]. Tính số đo của góc nhị diện \[\left[ {M,SO,D} \right]\].
![Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông, hai đường thẳng \[AC\] và \[BD\] cắt nhau tại \[O\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid13-1736516787.png)
A. \(175^\circ \).
B. \(135^\circ \).
C. \(45^\circ \).
D. \(90^\circ \).
Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng có quan hệ gì với mặt phẳng thứ ba?
A. Song song với mặt phẳng thứ ba.
B. Nằm trong với mặt phẳng thứ ba.
C. Cắt nhưng không vuông góc với mặt phẳng thứ ba.
D. Vuông góc với mặt phẳng thứ ba.
Cho hình lập phương \[ABCD.A'B'C'D'\]. Mệnh đề nào sau đây đúng ?
![Cho hình lập phương \[ABCD.A'B'C'D'\]. Mệnh đề nào sau đây đúng ? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid14-1736516938.png)
A.\[\left( {ADD'A'} \right) \bot \left( {BCC'D'} \right)\].
B. \[\left( {ADD'A'} \right) \bot \left( {ACC'A'} \right)\].
C. \[\left( {ADD'A'} \right) \bot \left( {BDD'B'} \right)\].
D. \[\left( {ADD'A'} \right) \bot \left( {ABCD} \right)\].
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(\sqrt 2 a\), \(O = AC \cap BD, \)\(SO \bot \left( {ABCD} \right)\), tam giác \(SAC\) vuông cân tại \(S\). Khoảng cách từ điểm \(S\) đến mặt phẳng \(\left( {ABCD} \right)\) bằng
A.\(a\).
B. \(a\sqrt 2 \).
C.\(\frac{{a\sqrt 2 }}{2}\).
D. \(2a\).
Cho hình chóp tam giác \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(SA \bot \left( {ABCD} \right)\). Mệnh đề nào sau đây đúng?
A.\(\left( {SBC} \right) \bot \left( {SAC} \right)\).
B. \(\left( {SBC} \right) \bot \left( {SCD} \right)\).
C.\(\left( {SBC} \right) \bot \left( {SAB} \right)\).
D. \(\left( {SBC} \right) \bot \left( {SBD} \right)\).
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right), SA = a\). Tam giác \(ABC\) vuông cân tại \(A\), cạnh \(AB = a\sqrt 2 \). Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right)\).
A.\(\sqrt 3 a\).
B. \(\frac{{\sqrt 3 }}{2}a\).
C.\(\frac{{\sqrt 2 }}{2}a\).
D. \(\sqrt 2 a\).
Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình thang vuông tại \(A,D\). Góc giữa \(SB\) và \(\left( {ABCD} \right)\) bằng \(45^\circ \). Biết rằng \(SA \bot \left( {ABCD} \right)\), \(SA = 2AD = 2DC = 2a\). Khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng
A. \[\frac{{2a\sqrt 3 }}{3}\].
B. \[\frac{{a\sqrt 3 }}{3}\].
C. \[\frac{{2a\sqrt 5 }}{5}\].
D. \[\frac{{a\sqrt 5 }}{5}\].
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\). Đường vuông góc chung của hai đường thẳng chéo nhau \(AB\) và \(B'C'\) là
A. \(BC\).
B. \(BB'\).
C. \(CC'\).
D. \(A'B'\).
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AA' = 2a\), \(A'B' = 2a\), \(A'D' = a\). Khoảng cách từ đường thẳng \(AA'\) đến mặt phẳng \(\left( {BDD'B'} \right)\) bằng:
A.\(\frac{{2a\sqrt 5 }}{5}\).
B. \(a\sqrt 2 \).
C. \(\frac{a}{2}\).
D. \(\frac{{a\sqrt 2 }}{2}\).
Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình thoi cạnh \(a\), \(\widehat {BAD} = 60^\circ \). Hình chiếu vuông góc của \(S\) trên mặt phẳng đáy là giao điểm \(O\) của \(AC\) và \(BD\). Góc nhị diện \(\left[ {S,CD,A} \right]\) có số đo bằng \(60^\circ \). Khoảng cách giữa \(AB\) và \(SC\) bằng
A. \(\frac{a}{2}\).
B. \(\frac{{3a}}{4}\).
C. \(\frac{a}{4}\).
D. \(\frac{{2a}}{3}\).
Một hình chóp tứ giác đều có thể tích \[200\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\], chiều cao \[12\,{\rm{cm}}\]. Diện tích đáy của hình chóp bằng:
A.\(25\,{\rm{c}}{{\rm{m}}^2}\).
B. \(50\,{\rm{c}}{{\rm{m}}^2}\).
C. \(75\,{\rm{c}}{{\rm{m}}^2}\).
D. \(\frac{{50}}{3}\,{\rm{c}}{{\rm{m}}^2}\).
Cho khối hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AA' = a,{\rm{ }}AB = 3a,{\rm{ }}AC = 5a\). Thể tích khối hộp đã cho là
A.\(5{a^3}\).
B.\(4{a^3}\).
C.\(12{a^3}\).
D.\(15{a^3}\).
Hình chóp tam giác đều \(S.ABC\) có cạnh đáy bằng \(3a\), cạnh bên bằng \(2\sqrt 3 a\). Gọi \[G\] là trọng tâm của tam giác \[ABC\], tính độ dài đoạn thẳng \[SG\].
A. \(SG = a\).
B. \(SG = 3a\).
C. \(SG = \frac{{3a}}{2}\).
D. \(SG = a\sqrt 3 \).
Cho hình chóp đều \[S.ABC\] có cạnh đáy bằng \[a\], cạnh bên bằng \[\frac{{a\sqrt {21} }}{6}\]. Tính theo \(a\) thể tích \(V\) của khối chóp \[S.ABC\].
A.\[V = \frac{{{a^3}\sqrt 3 }}{8}\].
B. \[V = \frac{{{a^3}\sqrt 3 }}{{12}}\].
C. \[V = \frac{{{a^3}\sqrt 3 }}{{24}}\].
D. \[V = \frac{{{a^3}\sqrt 3 }}{6}\].
Tính thể tích \[V\] của khối lăng trụ tam giác đều có cạnh đáy bằng \[a\] và tổng diện tích các mặt bên bằng \[3{a^2}.\]
A. \(V = \frac{{{a^3}\sqrt 3 }}{6}\).
B. \(V = \frac{{{a^3}\sqrt 3 }}{{12}}\).
C. \(V = \frac{{{a^3}\sqrt 2 }}{3}\).
D. \(V = \frac{{{a^3}\sqrt 3 }}{4}\).
Cho hình hộp \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình thoi có cạnh bằng \(2a\) và góc \(\widehat {ABC} = 60^\circ \), cạnh bên \(AA'\)bằng \(\frac{{4a}}{{\sqrt 3 }}\); \(A'\) cách đều các đỉnh\(A,B,C\). Tính theo \(a\) thể tích của khối hộp \(ABCD.A'B'C'D'\).
A. \(4{a^3}\sqrt 3 \).
B. \(2{a^3}\sqrt 3 \).
C. \(16{a^3}\sqrt 3 \).
D. \(8{a^3}\sqrt 3 \).
Cho hình chóp cụt tam giác, trong đó 2 mặt đáy là 2 tam giác đều có cạnh lần lượt là \(4\;{\rm{cm}}\) và \(2\;{\rm{cm}}\), chiều cao hình chóp là \(6\;{\rm{cm}}\). Thể tích của hình chóp cụt đó bằng:
A.\(14\sqrt 3 \,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
B.\(2\sqrt 3 \,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
C.\(3\sqrt 3 \,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
D.\(8\sqrt 3 \,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
Tính thể tích của hình chóp cụt đều có đáy lớn là hình vuông, cạnh \(6\;\,{\rm{cm}}\), đáy nhỏ là hình vuông cạnh \(3\;\,{\rm{cm}}\) và chiều cao của hình chóp cụt là \(4\,\;{\rm{cm}}\).
A.\(84\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
B.\(32\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
C.\(12\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
D.\(96\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), mặt bên \(SAB\) là tam giác cân tại \(S\) và nằm trong mặt phẳng vuông góc với đáy; góc giữa \(SC\) và mặt phẳng đáy bằng \(45^\circ \). Thể tích khối chóp \(S.ABCD\)bằng:
A. \[\frac{{{a^3}\sqrt 3 }}{{12}}\].
B. \[\frac{{{a^3}\sqrt 3 }}{9}\].
C. \[\frac{{{a^3}\sqrt 5 }}{{24}}\].
D. \[\frac{{{a^3}\sqrt 5 }}{6}\].
Cho lăng trụ đều \(ABC.A'B'C'\). Biết rằng góc nhị diện \(\left[ {A,BC,A'} \right]\) có số đobằng \(30^\circ \), tam giác \(A'BC\)có diện tích bằng \(8\). Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng
A. \(8\sqrt 3 \).
B. \(8\).
C. \(3\sqrt 3 \).
D. \(8\sqrt 2 \).

