50 CÂU HỎI
Cho hàm số có đồ thị (C). Biết đồ thị (C )có ba điểm cực trị A, B, C và ABDC là hình thoi, trong đó D(0;-3), A thuộc trục tung. Khi đó m thuộc khoảng nào?
A.
B.
C.
D.
Cho hàm số có đồ thị (C). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến có hệ số góc k= -9
A. y+16= -9(x+3)
B. y-16= -9(x-3)
C. y= -9(x+3)
D. y-16= -9(x+3)
Cho số phức thỏa mãn |z-2i| |z-4i| và |z-3-3i|=1. Giá trị lớn nhất của P=|z-2| là
A. c
B.
C.
D.
Tiệm cận đứng của đồ thị hàm số y=là
A. x= -2
B. Không có tiệm cận đứng
C. x= -1;x= -2
D. x= -1
Cho hình chóp S.ABC có SA=SB=SC=AB=AC=a, BC=. Tính số đo của góc (AB;SC) ta được kết quả
A.
B.
C.
D.
Nghiệm của phương trình =0 là
A.
B.
C.
D.
Trong tập các số phức, cho phương trình , m∈R (1). Gọi là một giá trị của m để phương trình (1) có hai nghiệm phân biệt x thỏa mãn . Hỏi trong khoảng (0;20) có bao nhiêu giá trị m
A. 13
B. 11
C. 12
D. 10
Cho hàm số y= . Nghiệm của phương trình y'.y=2x+1 là
A. x= 2
B. x= 1
C. Vô nghiệm
D. x= -1
Gọi số phức z= a+bi (a,b∈ R) thỏa mãn |z-1|= 1 và có phần thực bằng 1 đồng thời z không là số thực. Khi đó a.b bằng
A. ab= -2
B. ab= 2
C. ab= 1
D. ab= -1
Tìm hệ số của trong khai triển P(x)=
A. 1715
B. 1711
C. 1287
D. 1716
Cho hàm số y=x+sin2 x+2017. Tìm tất cả các điểm cực tiểu của hàm số
A.
B.
C.
D.
Nghiệm của phương trình cos(x+π/4)= là
A.
B.
C.
D.
Cho lăng trụ ABC.A'B'C'. Gọi M, N lần lượt là trung điểm của A 'B' và CC'. Khi đó CB' song song với
A. AM
B. A'N
C. (BC'M)
D. (AC'M)
Cho hình chóp S.ABCD, đáy là hình thang vuông tại A và B, biết AB=BC=a,AD=2a,SA= (ABCD). Gọi M và N lần lượt là trung điểm của SB,SA. Tính khoảng cách từ M đến (NCD) theo a
A.
B.
C.
D.
Số tiệm cận ngang của đồ thị hàm số y= là
A. 2
B. 3
C. 0
D. 1
Tìm m để đường thẳng y= x+m (d) cắt đồ thị hàm số y= (C) tại hai điểm phân biệt thuộc hai nhánh của đồ thị (C)
A.
B.
C.
D.
Tìm tập xác định D của hàm số y=tan2x
A.
B.
C.
D.
Xét khối tứ diện ABCD,AB= x, các cạnh còn lại bằng . Tìm x để thể tích khối tứ diện ABCD lớn nhất
A.
B.
C.
D.
Cho các hàm số (I):; (II):; (III):y= (IV):y=. Các hàm số không có cực trị là
A.(I),(II),(III)
B. (III),(IV),(I)
C. (IV),(I),(II)
D. (II),(III),(IV)
Chọn phát biểu đúng
A. Các hàm số y=sinx,y=cosx,y=cotx đều là hàm số chẵn
B. Các hàm số y=sinx,y=cosx,y=cotx đều là hàm số lẻ
C. Các hàm số y=sinx,y=cotx,y=tanx đều là hàm số chẵn
D. Các hàm số y=sinx,y=cotx,y=tanx đều là hàm số lẻ
Trên tập số phức, cho phương trình (a,b,c∈R;a≠0). Chọn kết luận sai
A. Nếu b=0 thì phương trình có hai nghiệm mà tổng bằng 0
B. Nếu thì phương trình có hai nghiệm mà modun bằng nhau
C. Phương trình luôn có hai nghiệm phức là liên hợp của nhau
D. Phương trình luôn có nghiệm
Cho hàm số y=f(x) xác định và có đạo hàm cấp một và cấp hai trên khoảng (a,b) và (a,b ). Khẳng định nào sau đây là sai?
A. ≠0 thì là điểm cực trị của hàm số
B. thì là điểm cực tiểu của hàm số
C. Hàm số đạt cực đại tại thì =0
D. thì không điểm cực trị của hàm số
Cho hàm số y=f(x) có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị của hàm số nào
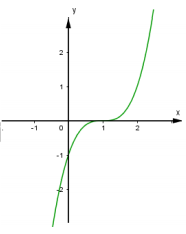
A.
B.
C.
D.
Cho số phức z thỏa mãn z(2-i)+13i=1. Tính mô đun của số phức z
A.
B.
C.
D.
Cho khối lăng trụ tam giác ABC.A'B'C' có thể tích là V. Gọi I, J lần lượt là trung điểm hai cạnh AA' và BB'. Khi đó thể tích của khối đa diện ABCIJC' bằng
A.
B.
C.
D.
Phương trình cos2x+4 sinx+5=0 có bao nhiêu nghiệm trên khoảng ()
A. 5
B. 4
C. 2
D. 3
Cho tứ diện ABCD có AB=AC=2,DB=DC=3. Khẳng định nào sau đây đúng
A.
B.
C.
D.
Cho khối chóp S.ABC có ,SA=a,SB=2a,SC=4a. Tính thể tích khối chóp S.ABC theo a
A.
B.
C.
D.
Cho số phức z thỏa mãn là số thực và |z-2|=m với m R. Gọi là một giá trị của m để có đúng một số phức thỏa mãn bài toán. Khi đó
A.
B.
C.
D.
Cho hàm số y= (m là tham số thực) thỏa mãn
Mệnh đề nào dưới đây đúng
A.
B.
C.
D.
Tìm góc {π/6;π/4;π/3;π/2} để phương trình cos2x+sin2x-2cosx= 0 tương đương với phương trình c
A.
B.
C.
D.
Một công ty muốn làm một đường ống dẫn dầu từ một kho A ở trên bờ biển đến một vị trí B trên hòn đảo. Hòn đảo cách bờ biển 6km. Gọi C là điểm trên bờ sao cho BC vuông góc với bờ biển. Khoảng cách từ A đến C là 9km. Người ta cần xác định một vị trí D trên AC để lắp ống dẫn theo đường gấp khúc ADB. Tính khoảng cách AD để số tiền chi phí thấp nhất, biết rằng giá để lắp mỗi km đường ống trên bờ là 100.000.000 đồng và dưới nước là 260.000.000 đồng
A. 7km
B. 6km
C. 7.5km
D. 6.5km
Người ta muốn xây một chiếc bể chứa nước có hình dạng là một khối hộp chữ nhật không nắp có thể tích bằng Biết đáy hồ là một hình chữ nhật có chiều dài gấp đôi chiều rộng và giá thuê thợ xây là 100.000 đồng . Tìm kích thước của hồ để chi phí thuê nhân công ít nhất. Khi đó chi phí thuê nhân công là
A. 15 triệu đồng
B. 11 triệu đồng
C. 13 triệu đồng
D. 17 triệu đồng
Biết rằng giá trị lớn nhất của hàm số . Giá trị của m là
A.
B.
C.
D.
Trong mặt phẳng phức, gọi M là điểm biểu diễn cho số phức với z= a+bi(a,). Chọn kết luận đúng
A. M thuộc tia Ox
B. M thuộc tia Oy
C. M thuộc tia đối của tia Ox
D. M thuộc tia đối của tia Oy
Trong tập các số phức, gọi là hai nghiệm của phương trình với có thành phần ảo dương. Cho số phức z thỏa mãn | |=1 Giá trị nhỏ nhất của P=| |là
A.
B.
C.
D.
Số mặt phẳng đối xứng của khối tứ diện đều là
A. 7
B. 8
C. 9
D. 6
Cho hàm số . Khẳng định nào sau đây đúng
A.
B. Đồ thị hàm số luôn cắt trục hoành
C. Hàm số luôn tăng trên R
D. Hàm số luôn có cực trị
Đội văn nghệ của nhà trường gồm 4 học sinh lớp 12A, 3 học sinh lớp 12B và 2 học sinh lớp 12C. Chọn ngẫu nhiên 5 học sinh từ đội văn nghệ để biểu diễn trong lễ bế giảng. Hỏi có bao nhiêu cách chọn sao cho lớp nào cũng có học sinh được chọn?
A. 120
B. 98
C. 150
D. 360
Có bao nhiêu số chẵn mà mỗi số có 4 chữ số đôi một khác nhau
A. 2520
B. 50000
C. 4500
D. 2296
Gọi S là tập hợp các số thực m sao cho với mỗi có đúng một số phức thỏa mãn là số thuần ảo. Tính tổng của các phần tử của tập S.
A. 10
B. 0
C. 16
D. 8
Tìm số phức z thỏa mãn |z-2|=|z| và (z+1)() là số thực
A.
B.
C.
D.
Cho hàm số . Để hàm số đạt cực trị tại thỏa mãn thì a thuộc khoảng nào
A.
B.
C.
D.
Tìm tất cả các giá trị của m để đồ thị hàm số y= có tiệm cận đứng
A.
B.
C.
D.
Tìm m để hàm số tăng trên khoảng (1;+∞)
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, K lần lượt là trung điểm của CD,CB,SA. Thiết diện của hình chóp cắt bởi mặt phẳng (MNK) là một đa giác (H). Hãy chọn khẳng định đúng
A. (H) là một hình thang
B. (H) là một ngũ giác
C. (H) là một hình bình hành
D. (H) là một tam giác
Tập giá trị của hàm số y=sin2x+cos2x+1 là đoạn [a;b]. Tính tổng T= a+b
A. c1
B. T= 2
C. T= 0
D. T= -1
Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất để được 3 quyển được lấy ra có ít nhất một quyển là toán
A.
B.
C.
D.
Cho hàm số y=f(x)=. Mệnh đề sai là
A. f không có đạo hàm tại
B. f'(1)=2
C. f'(0)= 2
D. f'(2)= 4
Nghiệm của phương trình tan3x=tanx là
A.
B.
C.
D.


