40 CÂU HỎI
Cho hình lập phương \[ABCD.A'B'C'D'\]. Vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương \[ABCD.A'B'C'D'\] và bằng vectơ \(\overrightarrow {AD} \) là
![Cho hình lập phương \[ABCD.A'B'C'D'\]. Vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid0-1737029811.png)
A. \[\overrightarrow {B'C'} \].
B. \[\overrightarrow {DA} \].
C. \[\overrightarrow {CB} \].
D. \[\overrightarrow {AB} \].
Cho hai vectơ \[\overrightarrow u ,\overrightarrow v \] có \[\left| {\overrightarrow u } \right| = 3,\left| {\overrightarrow v } \right| = 4\] và góc giữa hai vectơ \[\overrightarrow u ,\overrightarrow v \] bằng \[60^\circ \]. Tích vô hướng \[\overrightarrow u \cdot \overrightarrow v \] bằng
A. \[12\].
B. \[6\].
C. \[ - 12\].
D. \[ - 6\].
Trong không gian \(Oxyz\), cho vectơ \(\overrightarrow a = 3\overrightarrow i + 4\overrightarrow j - \overrightarrow k \). Tọa độ của vectơ \(\overrightarrow a \)là
A.\(\left( {3\;;\;4\;;\;1} \right)\).
B.\(\left( {3\;;\;0\;;\;1} \right)\).
C.\(\left( {3\;;\;4\;;\; - 1} \right)\).
D.\(\left( {3\;;\;0\;;\;0} \right)\).
Trong không gian \(Oxyz\), mặt phẳng đi qua điểm \(K\left( {1;\,\,1;\,\,1} \right)\) nhận \(\vec u = \left( {1;0;1} \right)\), \(\vec v = \left( {1;1;0} \right)\) là cặp vectơ chỉ phương có phương trình tổng quát là
A. \(x + y + z - 3 = 0\).
B. \(x - y + z - 1 = 0\).
C. \(x + y - z - 1 = 0\).
D. \( - x + y + z - 1 = 0\).
Cho đường thẳng \(\Delta \) có phương trình \(\left\{ \begin{array}{l}x = 3 - t\\y = - 1\\z = 3t\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right)\). Vectơ nào sau đây là vectơ chỉ phương của \(\Delta \)?
A.\({\vec u_1} = \left( {3; - 1;3} \right)\).
B. \({\vec u_2} = \left( {3; - 1;0} \right)\).
C. \({\vec u_3} = \left( { - 1; - 1;3} \right)\).
D. \({\vec u_4} = \left( { - 1;0;3} \right)\).
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\sqrt 2 ,\) chiều cao bằng \(2a\) và \(O\) là tâm của đáy. Bằng cách thiết lập hệ trục tọa độ \(Oxyz\) như hình vẽ bên, ta tính được khoảng cách từ điểm \(C\) đến mặt phẳng \(\left( {SAB} \right)\) bằng
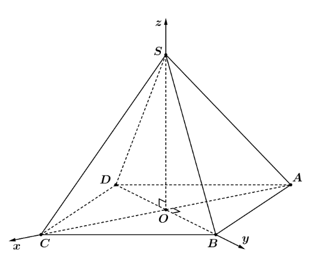
A. \(\frac{{2a}}{3}.\)
B. \(\frac{{2a}}{{\sqrt {17} }}.\)
C. \(\frac{{4a}}{{\sqrt {17} }}.\)
D. \(\frac{{4a}}{3}.\)
Trong không gian \(Oxyz\), mặt cầu tâm \(I\left( { - 6; - 9;15} \right)\), đường kính bằng 10 có phương trình là:
A. \({\left( {x + 6} \right)^2} + {\left( {y + 9} \right)^2} + {\left( {z - 15} \right)^2} = 100\).
B. \({\left( {x + 6} \right)^2} + {\left( {y + 9} \right)^2} + {\left( {z - 15} \right)^2} = 25\).
C. \({\left( {x - 6} \right)^2} + {\left( {y - 9} \right)^2} + {\left( {z + 15} \right)^2} = 100\).
D. \({\left( {x - 6} \right)^2} + {\left( {y - 9} \right)^2} + {\left( {z + 15} \right)^2} = 25\).
Cho tứ diện \(ABCD\), khi đó \(\overrightarrow {BD} - \overrightarrow {BC} \) bằng
A. \(\overrightarrow {DC} .\)
B. \(\overrightarrow {BA} .\)
C. \(\overrightarrow {CD} .\)
D. \(\overrightarrow {DB} .\)
Cho hình hộp \(ABCD.A'B'C'D'\). Mệnh đề nào sau đây đúng?
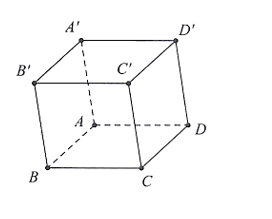
A. \(\overrightarrow {AC'} = \overrightarrow {AD} + \overrightarrow {AC} + \overrightarrow {AA'} .\)
B. \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} .\)
C. \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AA'} .\)
D. \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AC} .\)
Cho hình lăng trụ \(ABC.A'B'C'.\) Đặt \(\vec a = \overrightarrow {AA'} ,\vec b = \overrightarrow {AB} ,\vec c = \overrightarrow {AC} .\) Hãy biểu diễn vectơ \(\overrightarrow {B'C} \) theo các vectơ \(\vec a,\vec b,\vec c.\)
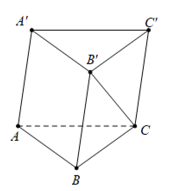
A. \(\overrightarrow {B'C} = \vec a + \vec b - \vec c.\)
B. \(\overrightarrow {B'C} = - \vec a + \vec b - \vec c.\)
C. \(\overrightarrow {B'C} = \vec a + \vec b + \vec c.\)
D. \(\overrightarrow {B'C} = - \vec a - \vec b + \vec c.\)
Cho hình lập phương \(ABCD.A'B'C'D'\). Gọi \(O\) là tâm của hình lập phương. Khẳng định nào dưới đây là đúng?
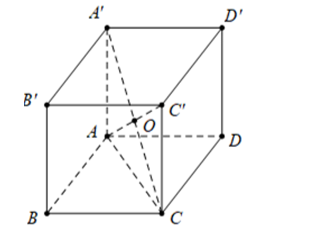
A. \(\overrightarrow {AO} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right).\)
B. \(\overrightarrow {AO} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right).\)
C. \(\overrightarrow {AO} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right).\)
D. \(\overrightarrow {AO} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right).\)
Cho hình hộp \(ABCD.A'B'C'D'\) có tâm \(O\). Đặt \(\overrightarrow {AB} = \vec a;\overrightarrow {BC} = \vec b,M\) là điểm xác định bởi \(\overrightarrow {OM} = \frac{1}{2}\left( {\vec a - \vec b} \right).\) Khẳng định nào sau đây đúng?
A.\(M\) là tâm hình bình hành \(ABB'A'.\)
B. \(M\) là tâm hình bình hành \(BCC'B'.\)
C.\(M\) là trung điểm \(BB'.\)
D.\(M\) là trung điểm \(CC'.\)
Trong không gian cho hai vectơ \(\vec u,\vec v\) tạo với nhau một góc \(60^\circ ,\,\,\left| {\vec u} \right| = 1\) và \(\left| {\vec v} \right| = 2.\) Tích vô hướng \(\vec u \cdot \vec v\) bằng
A. 1.
B. 2.
C. \(\sqrt 3 .\)
D. 3.
Cho hai vectơ \(\vec a\) và \(\vec b\) thỏa mãn \(\left| {\vec a} \right| = 3,\,\left| {\vec b} \right| = 2\) và \(\vec a \cdot \vec b = - 3.\) Xác định góc \(\alpha \) giữa hai vectơ \(\vec a\) và \(\vec b.\)
A. \(\alpha = 30^\circ .\)
B. \(\alpha = 45^\circ .\)
C. \(\alpha = 60^\circ .\)
D. \(\alpha = 120^\circ .\)
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Góc giữa hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {DA'} \) bằng
A.\(45^\circ .\)
B. \(90^\circ .\)
C. \(60^\circ .\)
D. \(120^\circ .\)
Cho hai vectơ \(\vec a,\vec b\) sao cho \(\left| {\vec a} \right| = \sqrt 2 ,\left| {\vec b} \right| = 2\) và hai vectơ \(\vec x = \vec a + \vec b,\) \(\vec y = 2\vec a - \vec b\) vuông góc với nhau. Tính góc giữa hai vectơ \(\vec a\) và \(\vec b.\)
A. \(120^\circ .\)
B. \(60^\circ .\)
C. \(90^\circ .\)
D. \(30^\circ .\)
Trong không gian cho hai vectơ \(\vec u\) và \(\vec v\) tạo với nhau một góc \(120^\circ \) và \(\left| {\vec u} \right| = 2,\,\,\left| {\vec v} \right| = 5.\) Tính \(\left| {\vec u + \vec v} \right|.\)
A.\(\sqrt {19} .\)
B. \( - 5\).
C. 7.
D. \(\sqrt {39} .\)
Cho tứ diện đều \(ABCD\) có các cạnh bằng \(a\), \(M\) là trung điểm của cạnh \(BC\). Tính \(\overrightarrow {AM} \cdot \overrightarrow {AD} .\)
A. \(\frac{1}{6}{a^2}.\)
B. \(\frac{1}{4}{a^2}.\)
C. \(\frac{1}{2}{a^2}.\)
D. \({a^2}.\)
Cho tứ diện đều \(ABCD\) có các cạnh bằng \(a\). Gọi \(M,\,N\) lần lượt là trung điểm các cạnh \(AB\) và \(CD\). Tính tích vô hướng \(\overrightarrow {CM} \cdot \overrightarrow {AN} .\)
A. \( - \frac{1}{3}{a^2}.\)
B. \( - \frac{1}{6}{a^2}.\)
C. \( - \frac{1}{2}{a^2}.\)
D. \( - \frac{1}{8}{a^2}.\)
Trong không gian \(Oxyz\), cho đoạn thẳng \(AB\) có \(A\left( {3\;;\;1\;;\; - 1} \right)\)và \(B\left( { - 1\;;\;5\;;\;7} \right)\). Tọa độ trung điểm \(M\)của \(AB\) là
A.\(M\left( {2\;;\;6\;;\;6} \right)\).
B.\(M\left( {1\;;\;3\;;\;3} \right)\).
C.\(M\left( { - 1\;;\;3\;;\; - 3} \right)\).
D.\(M\left( { - 2\;;\; - 6\;;\; - 6} \right)\).
Trong không gian \(Oxyz\), cho \(\vec a = \left( {2; - 3;3} \right)\), \(\vec b = \left( {0;2; - 1} \right)\), \(\vec c = \left( {3; - 1;5} \right)\). Tìm tọa độ của vectơ \(\vec u = 2\vec a + 3\vec b - 2\vec c\).
A. \(\left( {10; - 2;13} \right)\).
B. \(\left( { - 2;2; - 7} \right)\).
C. \(\left( { - 2; - 2;7} \right)\).
D. \(\left( { - 2;2;7} \right)\).
Cho tứ giác \(ABCD\) biết \(A\left( {0;\, - 2;\,1} \right),\,\,B\left( {1;\,3;\, - 2} \right),\,\,C\left( {1;\,0;\,0} \right)\). Tìm tọa độ điểm \(D\) để tứ giác \(ABCD\) là hình bình hành.
A. \(D\left( {0;\, - 5;\,3} \right)\).
B. \(D\left( {0;\,5;\,3} \right)\).
C. \(D\left( {1;\,5;\, - 3} \right)\).
D. \(D\left( {0;\, - 5;\, - 3} \right)\).
Trong không gian với hệ tọa độ \[Oxyz\], cho \[\overrightarrow {OM} = \left( {1;5;2} \right)\], \[\overrightarrow {ON} = \left( {3;7; - 4} \right)\], \(K\left( { - 1;3;1} \right)\). Gọi \[P\] là điểm đối xứng với \[M\] qua \[N\]. Tìm tọa độ vectơ \[\overrightarrow {KP} \].
A. \(\overrightarrow {KP} = \left( {6;6; - 11} \right)\).
B. \[\overrightarrow {KP} = \left( {8;6; - 11} \right)\].
C. \[\overrightarrow {KP} = \left( {6;6; - 4} \right)\].
D. \[\overrightarrow {KP} = \left( {3;3; - 2} \right)\].
Trong không gian với hệ tọa độ \[Oxyz\], cho hai điểm \(A\left( { - 1; - 1;0} \right),B\left( {3;1; - 1} \right).\) Điểm \(M\) thuộc trục \(Oy\) và cách đều hai điểm \(A,\,B\) có tọa độ là
A. \(M\left( {0; - \frac{9}{4};0} \right).\)
B. \(M\left( {0;\frac{9}{2};0} \right).\)
C. \(M\left( {0; - \frac{9}{2};0} \right).\)
D. \(M\left( {0;\frac{9}{4};0} \right).\)
Trong không gian \[Oxyz\], cho \(A\left( {2;1; - 1} \right),B\left( {3;0;1} \right).\) Tìm điểm \(C \in Oz\) sao cho tam giác \(ABC\) vuông tại \(B\).
A. \(C\left( {0;\frac{3}{2};0} \right).\)
B. \(C\left( {0;0;\frac{5}{2}} \right).\)
C. \(C\left( {0;0;3} \right).\)
D. \(C\left( {0;0;5} \right).\)
Trong không gian với hệ tọa độ \[Oxyz\], cho ba điểm \(A\left( {1;3; - 2} \right),\)\(B\left( {0; - 1;3} \right),C\left( {m;n;8} \right)\) (với \(m,\,n\) là tham số). Tìm tất cả các giá trị của \(m,\,n\) để ba điểm \(A,\,B,\,C\) thẳng hàng.
A. \(m = 3,n = 11.\)
B. \(m = - 1,n = - 5.\)
C. \(m = - 1,n = 5.\)
D. \(m = 1,n = 5.\)
Trong không gian \[Oxyz\], cho \(\overrightarrow a = \,\left( { - 2;\,3;\,1} \right)\), \(\,\overrightarrow b = \left( {2;\, - 3;\,\,5} \right)\). Tìm tọa độ của \(\overrightarrow x = 2\overrightarrow a - 3\overrightarrow b \).
A. \(\overrightarrow x = \left( { - 10;\,\,15;\,\, - 13} \right)\).
B. \[\overrightarrow x = \left( {10;\,\, - 15;\,\,13} \right)\].
C. \(\overrightarrow x = \left( {2;\,\, - 3;\,\,17} \right)\).
D. \(\overrightarrow x = \left( { - 2;\,\,3;\,\, - 17} \right)\).
Trong không gian\(Oxyz\), cho tam giác \(ABC\) có \(A\left( {1; - 1;2} \right)\), \(B\left( {2; - 1;3} \right)\), \(C\left( {2;3;1} \right)\). Gọi \(G\)là trọng tâm tam giác \(ABC\), tọa độ điểm \(G\) là
A. \(G\left( {\frac{5}{3};\frac{1}{3}; - 2} \right)\).
B. \(G\left( {\frac{5}{2};\frac{1}{2};3} \right)\).
C. \(G\left( {5;1;6} \right)\).
D. \(G\left( {\frac{5}{3};\frac{1}{3};2} \right)\).
Trong không gian \(Oxyz\), vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng \(\left( P \right):x + 3y - 4z + 5 = 0\)?
A. \({\vec n_1} = \left( {3;4;5} \right)\).
B. \({\vec n_2} = \left( {1;3; - 4} \right)\).
C. \({\vec n_3} = \left( {1;3;4} \right)\).
D. \({\vec n_4} = \left( {3; - 4;5} \right)\).
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {3;\,2;\,1} \right),\,B\left( { - 1;\,4;\,1} \right),\,C\left( {3;\, - 2;\,5} \right)\). Tọa độ nào sau đây là tọa độ vectơ pháp tuyến của của mặt phẳng \(\left( {ABC} \right)\)?
A.\(\left( {1;\,2;\,2} \right)\).
B. \(\left( {8;\, - 16;\,16} \right)\).
C. \(\left( { - 1;\,2;\, - 2} \right)\).
D.\(\left( {1;\,4;\,4} \right)\).
Trong không gian \(Oxyz\), mặt phẳng nào sau đây đi qua gốc tọa độ?
A. \(x + 20 = 0\).
B. \(x - 2024 = 0\).
C. \(y + 2025 = 0\).
D. \(2x + 5y - 8z = 0\).
Trong không gian \[Oxyz\], cho mặt phẳng \[\left( P \right):\,2x + y - 2z + 4 = 0\]. Mặt phẳng nào sau đây vuông góc với \(\left( P \right)\)?
A. \(2x + y - 2z + 5 = 0\).
B. \(x + 2y + 2z - 5 = 0\).
C. \(x + 3y - z + 1 = 0\).
D. \(x + y + z - 6 = 0\).
Trong không gian \(Oxyz\), khoảng cách từ \(M\left( {1;2; - 3} \right)\) đến \(\left( P \right):x + 2y + 2z - 10 = 0\)là
A.\(3\).
B. \(\frac{2}{3}\).
C. \(\frac{4}{3}\).
D.\(\frac{{11}}{3}\).
Trong không gian \[Oxyz,\] cho \[A\left( {0;1;1} \right);\,B\left( {1;2;3} \right)\]. Viết phương trình mặt phẳng \[\left( P \right)\] đi qua \[A\] và vuông góc với đường thẳng \[AB.\]
A. \[\left( P \right):x + y + 2z - 3 = 0\].
B. \[\left( P \right):x + y + 2z - 6 = 0\].
C. \[\left( P \right):x + 3y + 4z - 7 = 0\].
D. \[\left( P \right):x + 3y + 4z - 26 = 0\].
Trong không gian \[Oxyz\], cho ba điểm\[A\left( {3; - 2; - 2} \right)\],\[B\left( {3;2;0} \right)\],\[C\left( {0;2;1} \right)\]. Phương trình mặt phẳng \[\left( {ABC} \right)\] là
A. \[2x - 3y + 6z + 12 = 0\].
B. \(2x + 3y - 6z - 12 = 0\).
C. \(2x - 3y + 6z = 0\).
D. \(2x + 3y + 6z + 12 = 0\).
Trong không gian \[Oxyz\], cho điểm \(A\left( {2; - 1; - 3} \right)\) và mặt phẳng \(\left( P \right):3x - 2y + 4z - 5 = 0.\) Mặt phẳng \[\left( Q \right)\] đi qua \[A\] và song song với mặt phẳng \[\left( P \right)\] có phương trình:
A. \(\left( Q \right):3x - 2y + 4z - 4 = 0.\)
B. \(\left( Q \right):3x - 2y + 4z + 4 = 0.\)
C. \(\left( Q \right):3x - 2y + 4z + 5 = 0.\)
D. \(\left( Q \right):3x + 2y + 4z + 8 = 0.\).
Trong không gian \(Oxyz\), mặt phẳng cắt ba trục tọa độ tại ba điểm \(D\left( {3;0;0} \right)\), \(E\left( {0; - 2;0} \right),\) \(G\left( {0;0; - 7} \right)\) có phương trình chính tắc là:
A. \(\frac{x}{3} - \frac{y}{2} - \frac{z}{7} + 1 = 0\).
B. \(\frac{x}{3} + \frac{y}{2} + \frac{z}{7} = 1\).
C. \(\frac{x}{3} - \frac{y}{2} - \frac{z}{7} = 1\).
D. \(\frac{x}{3} - \frac{y}{2} + \frac{z}{7} = 1\).
Trong không gian \(Oxyz\), vectơ nào sau đây là vectơ chỉ phương của đường thẳng \(\Delta :\frac{{x - 5}}{8} = \frac{{y - 9}}{6} = \frac{{z - 12}}{3}\).
A. \({\vec u_1} = \left( {8;6;3} \right)\).
B. \({\vec u_2} = \left( {8;6; - 3} \right)\).
C. \({\vec u_3} = \left( { - 8;6; - 3} \right)\).
D. \({\vec u_4} = \left( {5;9;12} \right)\).
Trong không gian \(Oxyz\), phương trình chính tắc của đường thẳng \(AB\) với \(A\left( {1;1;2} \right)\) và \(B\left( { - 4;3; - 2} \right)\) là:
A. \(\frac{{x + 4}}{1} = \frac{{y - 3}}{{ - 2}} = \frac{{z + 2}}{{ - 2}}\).
B. \(\frac{{x - 1}}{1} = \frac{{y - 1}}{{ - 2}} = \frac{{z - 2}}{{ - 2}}\).
C. \(\frac{{x + 1}}{{ - 5}} = \frac{{y + 1}}{2} = \frac{{z + 2}}{{ - 4}}\).
D. \(\frac{{x + 4}}{{ - 5}} = \frac{{y - 3}}{2} = \frac{{z + 2}}{{ - 4}}\).
Trong không gian \(Oxyz\), phương trình tham số của đường thẳng đi qua điểm \(A\left( {2;0; - 1} \right)\) và vuông góc với mặt phẳng \(\left( P \right):2x - y + z + 3 = 0\) là:
A. \(\left\{ \begin{array}{l}x = 2 + 2t\\y = - t\\z = - 1 + t\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right)\).
B. \(\left\{ \begin{array}{l}x = 2 + 2t\\y = - 1\\z = 1 - t\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right)\).
C. \(\left\{ \begin{array}{l}x = 2 + 2t\\y = - 1\\z = - 1 + t\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right)\).
D. \(\left\{ \begin{array}{l}x = 2 + 2t\\y = - t\\z = 1 - t\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right)\).

