35 CÂU HỎI
Đạo hàm của hàm số \(y = \sin 2x\) là
A. \(\cos 2x\).
B. \(2\cos 2x\).
C. \( - 2\cos 2x\).
D. \( - \cos 2x\).
Cho hàm số \(f\left( x \right) = \sqrt {{x^2} + 3} \). Tính giá trị của biểu thức \(S = f\left( 1 \right) + 4f'\left( 1 \right)\).
A. \(S = 2\).
B. \(S = 4\).
C. \(S = 6\).
D. \(S = 8\).
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:

Hàm số đã cho nghịch biến trên khoảng nào sau đây?
A. \(\left( {0;2} \right)\).
B. \(\left( {0; + \infty } \right)\).
C. \(\left( { - 2; - \infty } \right)\).
D. \(\left( {1;2} \right)\).
Giá trị lớn nhất của hàm số \(f\left( x \right) = 2 + 2x - {e^x}\) trên đoạn \(\left[ {0;2} \right]\) bằng
A. \(1\).
B. \(6 - {e^2}\).
C. \(\ln 2\).
D. \(2\ln 2\).
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} - x + 2}}{{x + 1}}\) có phương trình là
A. \(y = x - 2\).
B. \(y = x - 1\).
C. \(y = x + 1\).
D. \(x = - 1\).
Đường cong hình bên là của đồ thị hàm số \(y = a{x^3} + b{x^2} + cx + d\), khẳng định nào sau đây là đúng?
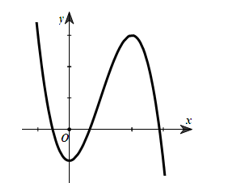
A. \(a > 0,\,d < 0\).
B. \(a < 0,\,d < 0\).
C. \(a < 0\,,\,d > 0\).
D. \(a > 0\,,d > 0\).
Đạo hàm của hàm số \(y = \sqrt {{x^2} + 2x} \)là
A. \(\sqrt {2x + 2} \).
B. \(\frac{x}{{2\sqrt {{x^2} + 2x} }}\).
C. \(\frac{1}{{2\sqrt {{x^2} + 2} }}\).
D. \(\frac{{x + 1}}{{\sqrt {{x^2} + 2x} }}\).
Đạo hàm của hàm số \(y = \frac{1}{2}\sin 2x + \cos x\)tại \({x_0} = \frac{\pi }{2}\)bằng
A. \( - 1\).
B. \(2\).
C. \(0\).
D. \( - 2\).
Một chuyển động có phương trình \(s\left( t \right) = {t^2} - 2t + 3\) (trong đó \(s\) tính bằng mét, \(t\) tính bằng giây). Vận tốc tức thời của chuyển động tại thời điểm \(t = 2s\) là
A. \(6 {\rm{m/s}}\).
B. \(4 {\rm{m/s}}\).
C. \(8 {\rm{m/s}}\).
D. \(2 {\rm{m/s}}\).
Cho hàm số \(f\left( x \right) = a{x^3} + \frac{b}{{{x^3}}} + c{x^2}\). Biết \(f\left( 2 \right) = \frac{{95}}{4}\), \[f'\left( 1 \right) = 16\], \[f'\left( { - 1} \right) = 8\]. Khi đó tổng \(a + b + c\) bằng
A. \(1\).
B. \(2\).
C. \(0\).
D. \(3\).
Cho hàm số bậc ba\(y = f\left( x \right)\)có đồ thị là đường cong nhưtrong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. \(\left( {0;2} \right)\).
B. \(\left( { - \infty ;0} \right)\).
C. \(\left( {1; + \infty } \right)\).
D. \(\left( { - 1;1} \right)\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ dưới.
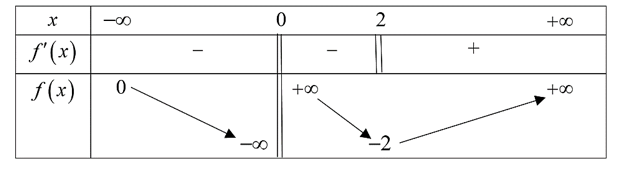
Mệnh đề nào sau đây sai?
A. Hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right)\) .
B. Hàm số nghịch biến trên khoảng \(\left( { - \infty ;2} \right)\).
C. Hàm số đồng biến trên khoảng \(\left( {2\,;\,5\,} \right)\).
D. Hàm số nghịch biến trên khoảng \(\left( {0;\,2} \right)\).
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{2x - 1}}{{x + 3}}\) là đường thẳng nào trong các đường thẳng dưới đây?
A. \(y = - 3\).
B. \(y = - 1\).
C. \(x = - 3\).
D. \(x = 2\).
Khẳng định nào sau đây đúng về tính đơn điệu của hàm số \[y = \frac{{2x + 4}}{{1 - x}}\]?
A. Hàm số đồng biến trên các khoảng \[\left( { - \infty ;1} \right)\] và \[\left( {1; + \infty } \right)\].
B. Hàm số nghịch biến trên các khoảng \[\left( { - \infty ;1} \right)\]\[ \cup \]\[\left( {1; + \infty } \right)\].
C. Hàm số nghịch biến trên các khoảng \[\left( { - \infty ;1} \right)\] và \[\left( {1; + \infty } \right)\].
D. Hàm số đồng biến trên các khoảng \[\left( { - \infty ; - 1} \right)\] và \[\left( { - 1; + \infty } \right)\].
Cho hàm số \(y = f\left( x \right)\) liên tục trên \[\mathbb{R}\] và có bảng xét dấu của \(f'\left( x \right)\) như sau:
![Cho hàm số \(y = f\left( x \right)\) liên tục trên \[\mathbb{R}\] và có bảng xét dấu của (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid0-1735913032.png)
Tìm số điểm cực trị của hàm số đã cho.
A. \(1\).
B. \(2\).
C. \(3\).
D. \(0\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên.
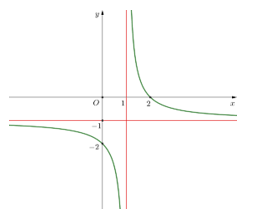
Đồ thị hàm số đã cho có đường tiệm cận ngang là
A. \(y = - 1\).
B. \(x = 1\).
C. \(x = 0\).
D. \(y = 1\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên trên đoạn \(\left[ {0;3} \right]\) như sau:
![Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên trên đoạn \(\left[ {0;3} \right]\) như sau: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid2-1735913256.png)
Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\)trên đoạn \(\left[ {0;3} \right]\) là
A. \(4\).
B. \(1\).
C. \(0\).
D. \( - \;4\).
Giá trị cực tiểu của hàm số \[y = f\left( x \right) = \frac{{{x^2} + x + 4}}{{x + 1}}\] là
A. \({y_{CT}} = - 5\).
B. \({y_{CT}} = 3\).
C. \({y_{CT}} = 1\).
D. \({y_{CT}} = - 3\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\), có đạo hàm \(f'\left( x \right) = 2x{\left( {x - 1} \right)^2}{\left( {2 - x} \right)^3}\). Tìm điểm cực tiểu của hàm số.
A. \(x = 1\).
B. \(x = 0\).
C. \(y = 0\).
D. \(x = 2\).
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x\left( {x - 1} \right){\left( {x + 4} \right)^3},\,\forall x \in \mathbb{R}\). Số điểm cực tiểu của hàm số đã cho là
A. \(2\).
B. \(3\).
C. \(4\).
D. \(1\).
Cho hàm số \(f\left( x \right)\) liên tục trên \(\left[ { - 1;5} \right]\) và có đồ thị như hình vẽ bên. Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên \(\left[ { - 1;5} \right]\). Giá trị của \(M - m\) bằng
![Cho hàm số \(f\left( x \right)\) liên tục trên \(\left[ { - 1;5} \right]\) và có đồ thị như hình vẽ bên (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid6-1735914131.png)
A. \(1\).
B. \(6\).
C. \(5\).
D. \(4\).
Giá trị lớn nhất \(M\) của hàm số \[y = {x^3} + 3x\] trên đoạn \[\left[ {0;2} \right]\] bằng
A. \[M = 0\].
B. \[M = 4\].
C. \[M = 14\].
D. \[M = - 2\].
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Mệnh đề nào dưới đây là đúng?
A. Hàm số có giá trị cực tiểu bằng \(2\).
B. Hàm số có ba điểm cực trị.
C. Hàm số có giá trị cực đại bằng \(0\).
D. Hàm số đạt cực đại tại \(x = 0\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Mệnh đề nào dưới đây là đúng?
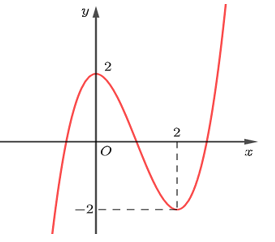
A. Hàm số có giá trị cực tiểu bằng \(2\).
B. Hàm số có ba điểm cực trị.
C. Hàm số có giá trị cực đại bằng \(0\).
D. Hàm số đạt cực đại tại \(x = 0\).
Bảng biến thiên trong hình dưới là của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D. Hỏi hàm số đó là hàm số nào?
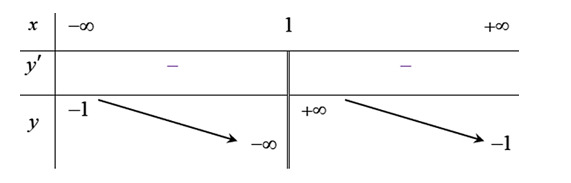
A. \(y = \frac{{x + 3}}{{x - 1}}\).
B. \(y = \frac{{ - x - 2}}{{x - 1}}\).
C. \(y = \frac{{ - x + 3}}{{x - 1}}\).
D. \(y = \frac{{ - x - 3}}{{x - 1}}\).
Bảng biến thiên sau là của hàm số nào trong các hàm số ở các đáp án A, B, C, D?
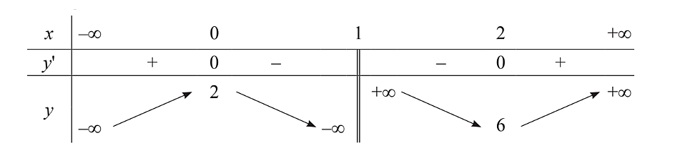
A. \(y = \frac{{{x^2} + 2x - 2}}{{x - 1}}\).
B. \(y = \frac{{{x^2} + 2x - 2}}{{x + 1}}\).
C. \(y = \frac{{{x^2} + 2x + 2}}{{x - 1}}\).
D. \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\).
Giá trị nhỏ nhất của hàm số \(y = x + \frac{9}{x}\) trên đoạn \(\left[ {2\,;\,4} \right]\) là
A. \(\mathop {\min }\limits_{\left[ {2\,;\,4} \right]} y = 6\).
B. \(\mathop {\min }\limits_{\left[ {2\,;\,4} \right]} y = \frac{{13}}{2}\).
C. \(\mathop {\min }\limits_{\left[ {2\,;\,4} \right]} y = \frac{{25}}{4}\).
D. \(\mathop {\min }\limits_{\left[ {2\,;\,4} \right]} y = - 6\).
Giá trị cực tiểu của hàm số \(y = {x^2}\ln x\) là
A.\(\frac{1}{e}\).
B. \( - \frac{1}{e}\).
C. \( - \frac{1}{{2e}}\).
D. \(\frac{1}{{2e}}\).
Để hàm số\(y = - {x^4} + 6{x^2} + m\)đạt giá trị lớn nhất trên đoạn \(\left[ { - 1;1} \right]\) bằng 5 thì giá trị của tham số \(m\)bằng
A. \(0\).
B. \(5\).
C. \( - 5\).
D. \(1\).
Cho hàm số bậc ba \(f\left( x \right)\) có bảng biến thiên sau.
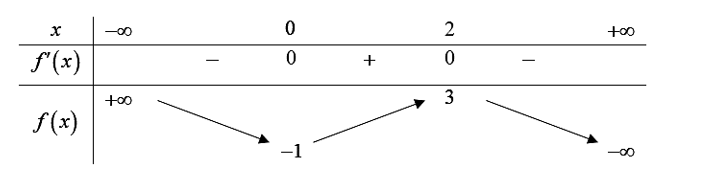
Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(f\left( x \right) = 2m + 1\) có ba nghiệm phân biệt?
A. 2.
B. 3.
C. 1.
D. 4.
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) (với \(a,b,c,d\) là số thực) có đồ thị như hình bên. Giá trị biểu thức \(T = \frac{{a - 2b + 3d}}{c}\) bằng
A. \(2\).
B. \(6\).
C. \( - 8\).
D. \(0\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
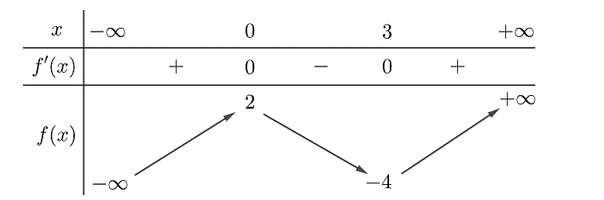
Bảng biến thiên trên là hàm số nào sau đây?
A. \(y = \frac{4}{9}{x^3} - 2{x^2} + 2\).
B. \(y = - \frac{4}{9}{x^3} + {x^2} + 2\).
C. \(y = {x^4} + 3{x^2} + 2\).
D. \(y = \frac{{x + 1}}{{x - 2}}\).
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình bên. Khẳng định nào sau đây đúng?
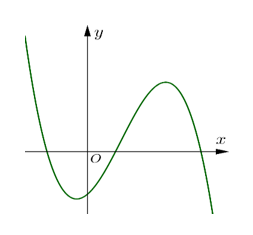
A. \(a < 0,b < 0,c < 0,d < 0\).
B. \(a < 0,b > 0,c > 0,d > 0\).
C. \(a < 0,b > 0,c < 0,d > 0\).
D. \(a < 0,b > 0,c > 0,d < 0\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
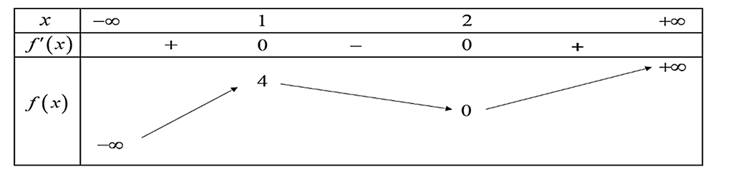
Có bao nhiêu giá trị nguyên của \(m\) với \(m \in \left( { - 3\,;\,2024} \right]\) để phương trình \(2f\left( x \right) - m = 0\) có một nghiệm?
A. \(2019\).
B. \(2020\).
C. \(2018\).
D. \(2021\).
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{{x + 2}}{{x + 5m}}\) đồng biến trên khoảng \(\left( { - \infty ; - 10} \right)?\)
A.\(0\).
B. \(1\).
C. \(3\).
D. \(2\).

