34 CÂU HỎI
Cho hai số phức Số phức là
A. z = -2 - 2i
B. z = -2 + 2i
C. z = 2 + 2i
D. z = 2 - 2i
Cho hai số phức Số phức là
A. w = -3 + 8i
B. w = -5 + i
C. w = -3 - 8i
D. w = -3 + i
Cho hai số phức Số phức là
A.
B. 1
C. 0
D.
Tất cả các số phức z thỏa mãn 2z - 3(1 + i) = iz + 7 - 3i là
A.
B. z = 4 - 2i
C.
D. z = 4 + 2i
Cho hai số phức . Số phức là
A. -4 + 2i
B. -4 - 2i
C. 4 - 2i
D. 4 + 2i
Cho số phức thỏa mãn . Giá trị của S = a - 3b là
A.
B. S = 3
C. S = -3
D.
Cho số phức z thỏa mãn (1 + i)z = 14 - 2i. Tổng phần thực và phần ảo của bằng
A. 14
B. 2
C. -2
D. -14
Cho hai số phức z = 3 + 2i và z' = a + (a2 - 11)i. Tất cả các giá trị thực của a để z + z' là một số thực là
A. a = -3
B. a = 3
C. a = 3 hoặc a = -3
D. hoặc
Cho số phức Số phức có phần ảo là
A. 2
B. 4
C. -2
D. 2i
Cho số phức z thỏa mãn z(2 - i) + 13i = 1. Mô đun của số phức z là
A.
B.
C.
D.
Cho số phức Số phức liên hợp của số phức là
A.
B.
C.
D.
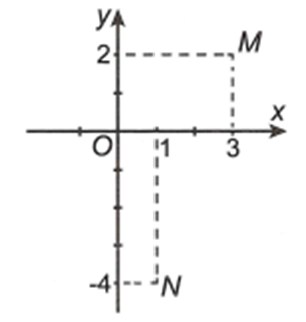
Gọi lần lượt có điểm biểu diễn là M và N trên mặt phẳng Oxy ở hình bên. Khi đó bằng
A.
B. 20
C.
D. 116
Cho số phức z = a + bi, với a, b là các số thực thỏa mãn a + bi + 2i(a - bi) + 4 = i, với i là đơn vị ảo. Môđun của là
A.
B.
C.
D.
Cho số phức z thỏa mãn Môđun của số phức là
A.
B.
C.
D.
Cho là các số phức thỏa mãn và Giá trị của biểu thức là
A. P = 2
B.
C. P = 3
D. P = 1
Điểm biểu diễn của số phức là
A. (3;-2)
B.
C. (-2;3)
D. (4;-1)
Gọi lần lượt có điểm biểu diễn là M, N trên mặt phẳng phức (hình bên). Khi đó phần ảo của số phức là
A.
B.
C.
D.
Cho số phức z thỏa mãn (1 + i)z = 11 - 3i. Điểm M biểu diễn cho số phức z trong mặt phẳng tọa độ là
A. M(4;-7)
B. M(14;-14)
C. M(8;-14)
D. M(7;-7)
Cho lần lượt là các điểm biểu diễn của các số phức Số phức có điểm biểu diễn D sao cho ABCD là hình bình hành là
A.
B.
C.
D.
Cho tam giác ABC có ba đỉnh A, B, C lần lượt là điểm biểu diễn hình học của các số phức Số phức z4 có điểm biểu diễn hình học là trọng tâm của tam giác ABC. Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
Cho các số phức thoả mãn . Gọi A, B lần lượt là các điểm biểu diễn số phức trên mặt phẳng toạ độ. Diện tích S của (với O là gốc toạ độ) là
A.
B. S = 6
C.
D. S = 12
Có bao nhiêu số phức z thỏa mãn
A. 1
B. 2
C. 3
D. 4
Có bao nhiêu số phức z thỏa điều kiện và
A. 2
B. 3
C. 1
D. 4
Có bao nhiêu số phức thỏa mãn
A. 2
B. 3
C. 1
D. 4
Có tất cả bao nhiêu giá trị nguyên của m để có đúng hai số phức z thỏa mãn và
A. 40
B. 41
C. 165
D. 164
Cho hai số phức z1 và z2 thỏa mãn Hỏi có bao nhiêu số z mà
A. 1
B. 2
C. 3
D. 4
Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn và . Số phần tử của S là
A. 2
B. 4
C. 1
D. 3
Có tất cả bao nhiêu số phức z thỏa mãn và
A. 3
B. 4
C. 6
D. 8
Xét các số phức z thỏa mãn là số thực. Biết rằng tập hợp tất cả các điểm biểu diễn của z là một đường tròn, có tâm I(a;b) và bán kính R. Giá trị a + b + R bằng
A. 6
B. 4
C. 12
D. 24
Cho số phức z thỏa mãn . Tập hợp các điểm biểu diễn số phức z là
A. Một parabol.
B. Một đường tròn.
C. Một elip.
D. Một hypebol.
Cho số phức z thỏa mãn và Tập hợp các điểm biểu diễn số phức w là đường tròn có tâm là
A. I(-3;-4)
B. I(3;4)
C. I(1;-2)
D. I(6;8)
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu biễn các số phức z thỏa mãn là đường thẳng có phương trình
A. x - 2y + 1 = 0
B. x + 2y = 0
C. x - 2y = 0
D. x + 2y + 1 = 0
Gọi M là điểm biểu diễn số phức z thỏa mãn Tập hợp tất cả các điểm M như vậy là
A. Một parabol.
B. Một đường thẳng.
C. Một đường tròn.
D. Một elip.
Cho số phức z thỏa mãn điều kiện Tập hợp các điểm biểu diễn của z tạo thành một hình phẳng. Diện tích của hình phẳng đó là
A.
B.
C.
D.

