30 đề thi thử THPT Quốc gia môn Toán năm 2022 có lời giải - Đề 21
50 câu hỏi
Đạo hàm của hàm số là
.
.
.
.
Đạo hàm của hàm số là
.
.
.
.
Thể tích khối chóp tứ giác đều có cạnh đáy bằng , chiều cao bằng 2a bằng
.
.
.
.
Tập xác định của hàm số là:
.
.
.
.
Cho cấp số cộng có 5 số hạng là . Công sai của cấp số cộng đã cho bằng
.
3.
-2.
-3.
Cho một cấp số nhân có . Số hạng bằng
-64.
-32.
64.
32.
Một tổ có 10 học sinh. Có bao nhiêu cách chọn ra 2 học sinh từ tổ đó để giữ hai chức vụ tổ trưởng và tổ phó?
.
.
.
.
Cho hàm số y=f(x) xác định trên và có bảng biến thiên như hình vẽ.
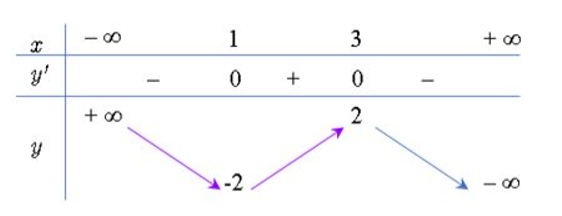
Kết luận nào sau đây là đúng?
Hàm số đồng biến trên .
Hàm số nghịch biến trên .
Hàm số đồng biến trên các khoảng và .
Hàm số đồng biến trên (1;3).
Mười đường thẳng có nhiều nhất bao nhiêu giao điểm ?
90.
45.
.
.
Tập xác định của hàm số là
.
.
.
.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Biết và . Thể tích của khối chóp S.ABCD bằng
.
.
.
Khối đa diện đều loại {5;3} có số mặt là
20
8.
15.
12.
Cho hàm số y= f(x) có bảng biến thiên như sau
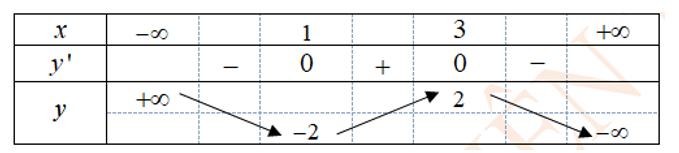
Hàm số đạt cực tiểu tại điểm
x = 1.
x = -2.
x = 2.
x =3.
Cho a là số thực dương khác 1. Khi đó bằng
5.
-5.
.
1.
Cho lăng trụ đứng ABC.A'B'C' có ; đáy ABC là tam giác vuông cân tại . Thể tích của khối lăng trụ ABC.A'B'C' bằng
.
.
.
.
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng 2a. Cạnh bên AA'= 4a. Thể tích của khối lăng trụ ABC.A'B'C' bằng
.
.
.
.
Cho khối hộp chữ nhật ABCD.A'B'C'D' có Thể tích của khối hộp chữ nhật đã cho bằng
24.
8.
12.
4.
Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số ?
.
.
.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông; hình chiếu của S trên (ABCD) trùng với trung điểm H của cạnh AB; kí hiệu là diện tích của hình vuông ABCD. Công thức tính thể tích của khối chóp S.ABCD là
.
.
.
.
Cho . Khi đó biểu diễn theo 5 là
.
.
.
.
Hàm số nào sau đây có bảng biến thiên như hình bên dưới?
.
.
.
.
Đường cong bên dưới là của đồ thị hàm số nào trong các hàm số sau đây?
.
.
.
.
Cho hàm số y=f(x) có và . Khẳng định nào sau đây ĐÚNG?
Đồ thị hàm số không có tiệm cận ngang.
Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng x = 2 và x =-2.
Đồ thị hàm số có đúng một tiệm cận ngang.
Đồ thị hàm số có hai tiệm cận ngang là các đường thẳng y = 2 và y = -2.
Tìm số giao điểm của đường cong và đường thẳng bẳng
0.
3.
2.
1.
Cho hàm số y= f(x) xác định và liên tục trên R có bảng xét dấu đạo hàm như sau:

Mệnh đề nào sau đây đúng?
.
.
.
.
Cho hàm số y=f(x) có đạo hàm . Mẹnh đề nào dưới đây đúng?
Hàm số nghịch biến trên các khoảng và .
Hàm số đồng biến trên các khoảng và .
Hàm số đồng biến trên các khoảng .
Hàm số nghịch biến trên các khoảng .
Cho với a,b là các số thực dượng lớn hơn 1. Khi đó bằng
.
.
.
.
Cho hàm số y= f(x) có đạo hàm . Mệnh đề nào dưới đây đúng?
Hàm số nghịch biến trên các khoảng và .
Hàm số đồng biến trên các khoảng và .
Hàm số đồng biến trên khoảng .
Hàm số nghịch biến trên khoảng .
Tập hợp tất cả các giá trị thực của tham số m để hàm số đạt cực tiểu tại x =0.
.
.
.
.
Cho tứ diện hình chóp S.ABCD có đáy ABC là tam giác vuông cân tại A, BC=4a. Mặt bên SBC là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABCD là
.
.
.
.
Cho hàm số f(x) có bảng biến thiên ở hình vẽ sau:
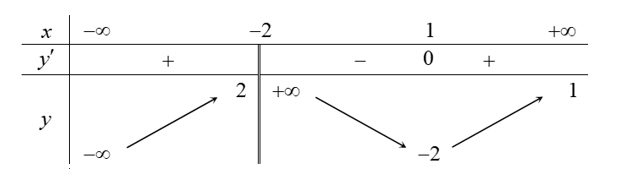
Số nghiệm của phương trình là
4.
3.
5.
2.
Biết rằng đồ thị hàm số có hai điểm cực trị là và A(0;2). Khi đó f(3) bằng
60.
-28.
11.
155.
Cho hình lăng trụ ABC.A'B'C' có hai đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trung điểm cạnh BC. Góc giữa BB' và mặt phẳng (ABC) bằng . Thể tích khối lăng trụ bằng
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và . Biết và Góc gữa hai mặt phẳng (SBC) và (ABC) bằng:
Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn lần lượt là M và m. Giá trị của bằng?
76.
.
66.
49.
Cho hàm số y = f(x) có đồ thị như hình vẽ. Số giá trị nguyên dương của tham số m để phương trình có 2 nghiệm là
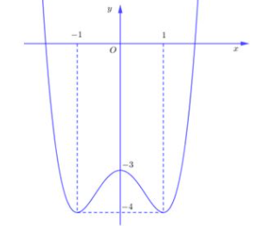
2024.
2021.
2020.
2023.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cùng hợp với đáy một góc . Góc hợp bởi đường thẳng SC với mặt phẳng (SBD) bằng
.
.
.
.
Cho hàm số y = f(x) xác định trên , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
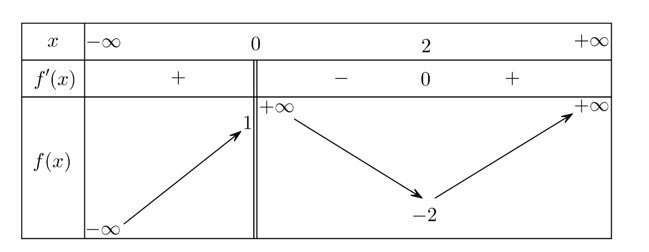
Tập hợp tất cả các giá trị của tham số thực m sao cho phương trình có đúng 3 nghiệm thực phân biệt là
Cho hàm số . Tập giá trị của hàm số f'(x) là
.
.
.
.
Có bao nhiêu giá trị nguyên m để đồ thị hàm số có 3 đường tiệm cận?
1.
0.
2.
7.
Cho hình chóp S.ABC có , đáy là tam giác đều cạnh a. Biết , khoảng cách từ trung điểm của SA đến mặt phẳng (SBC) bằng
.
.
.
.
Một đoàn khách có 8 người bước ngẫu nhiên vào một cửa hàng có 3 quầy. Xác suất đề quầy thứ nhất có 3 khách ghé thăm là
.
.
.
.
Để dự báo dân số của một quốc gia, người ta sử dụng công thức trong đó A là dân số của năm lấy làm mốc tính, S là dân số sau n năm, r là tỉ lệ gia tăng dân số hằng năm. Năm 2019 dân số Việt Nam là 96208984 người. Giả sử tỉ lệ tăng dân số hằng năm không đổi là hỏi đến năm nào dân số Việt Nam đạt mức 120 triệu người?
2040.
2035.
2050.
2035.
Cho hình chóp S.ABCD có đáy ABCD là hình thang có đáy lớn là AD các đường thẳng SA,AC và CD đôi một vuông góc với nhau; và Khoảng cách giữa hai đường thẳng SB và CD bằng
.
.
.
.
Cho hàm số có bảng biến thiên như sau :
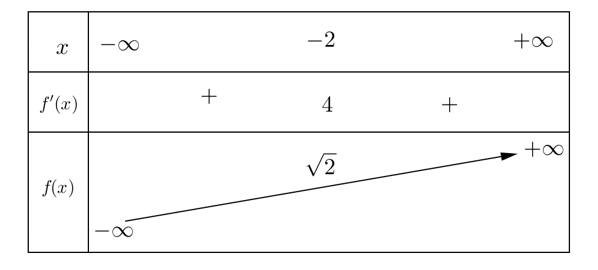
Có bao nhiêu số dương trong các hệ số a,b,c?
2.
0.
3.
1.
Cho khối tứ diện đều ABCD cạnh bằng 2cm. Gọi M,N,P lần lược là trọng tâm của ba tam giác . Thể tích V của khối chóp AMNP là
.
.
.
.
Cho hàm số . Số giá trị nguyên của m để hàm số nghịch biến trên R là
3
2
1
4
Cho hàm số y= f(x) có bảng biến thiên như sau
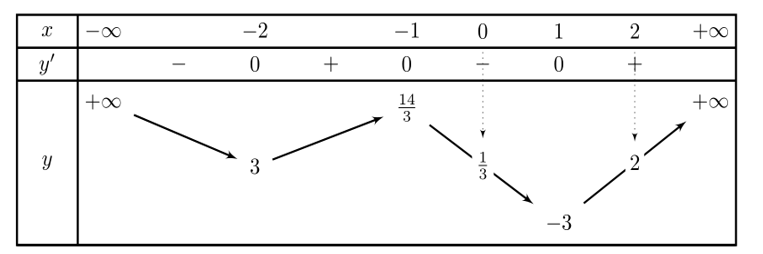
Số nghiệm thuộc đoạn của phương trình là
2020
2021
4
3
Xét hàm số , với m là tham số thực. Có bao nhiêu số nguyên m thỏa mãn điều kiện ?
6.
7.
4.
5.
Cho hàm số f(x) có đạo hàm trên R và có bảng biến thiên như sau:
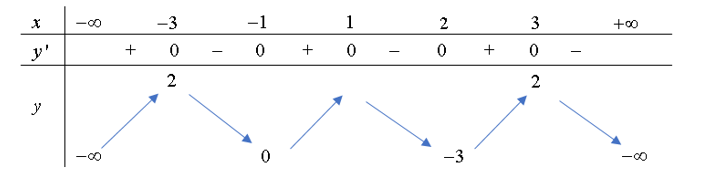
Số điểm cực đại của hàm số là
6.
8
7.
9.