50 CÂU HỎI
Cho số phức . Số phức liên hợp của z có điểm biểu diễn hình học là:
A. (-6;-7)
B. (6;7)
C. (6;-7)
D. (-6';7)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình . Tìm tọa độ tâm I và bán kính R của mặt cầu đó.
A.
B.
C.
D.
Biết F(x) là một nguyên hàm của hàm số và . Tính
A.
B.
C.
D.
Có bao nhiêu giá trị nguyên của tham số m trên để hàm số đồng biến trên khoảng ?
A. 6
B. 5
C. 7
D. 4
Cho hàm số có đồ thị như Hình 1. Đồ thị Hình 2 là của hàm số nào dưới đây?
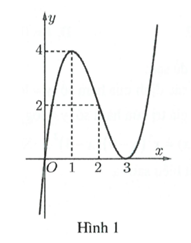
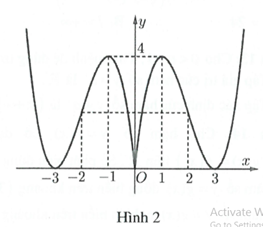
A.
B.
C.
D.
Nếu z = i là một nghiệm của phương trình với thì a+b bằng
A. 2
B. -1
C. 1
D. -2
Cho tập hợp . Số các tập con của tập X có chứa chữ số 0 là
A. 511.
B. 1024.
C. 1023.
D. 512.
Cho khối lăng trụ tam giác đều có cạnh đáy bằng 2, diện tích tam giác A'BC bằng 3. Tính thể tích của khối lăng trụ
A.
B.
C.
D.
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng và đường thẳng . Viết phương trình đường thẳng nằm trong mặt phẳng (P), đồng thời cắt và vuông góc với đường thẳng d.
A.
B.
C.
D.
Tìm hệ số của số hạng chứa trong khai triển biểu thức
A. 240
B. -240
C. -810
D. 810
Trong không gian Oxyz, phương trình mặt phẳng (P) đi qua điểm đồng thời vuông góc với hai mặt phẳng và là
A.
B.
C.
D.
Cho f(x) là một đa thức thõa mãn . Tính .
A. I = 24
B.
C. I = 2
D. I = 0
Cho 0 < a < 1. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Tập giá trị của hàm số là
B. Tập xác định của hàm số là
C. Tập xác định của hàm số là
D. Tập giá trị của hàm số là
Cho hàm số y = f(x) có đạo hàm . Xét hàm số trên R. Số phát biểu đúng trong các phát biểu sau là
I. Hàm số đồng biến trên khoảng
II. Hàm số nghịch biến trên khoảng
III. Hàm số có 5 điểm cực trị
IV.
A. 1
B. 2
C. 3
D. 4
Cho hai số phức có điểm biểu diễn lần lượt là cùng thuộc đường tròn có phương trình và . Tính giá trị biểu thức
A.
B.
C.
D.
Cho . Tính
A. 7
B. 8
C. -1
D. 5
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy và SA = 2a. Tính cosin góc giữa đường thẳng SB và mặt phẳng (SAD)
A.
B.
C.
D. 1
Trong không gian Oxyz, cho hai đường thẳng và . Khẳng định nào sau đây đúng?
A. cắt và không vuông góc với
B. và chéo nhau và vuông góc nhau
C. và song song nhau
D. cắt và vuông góc với
Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau?
A. 1000
B. 720
C. 729
D. 648
Gọi là nghiệm phức có phần ảo âm của phương trình . Tính
A. 25
B.
C. 5
D. 13
Cho hàm số có đồ thị (C) và điểm I(1;2). Điểm M(a;b) thuộc (C) với sao cho tiếp tuyến tại M của (C) vuông góc với đường thẳng IM. Giá trị của tổng bằng:
A. 1
B. 2
C. 4
D. 5
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng lần lượt có phương trình . Mặt phẳng cách đều hai đường thẳng có phương trình là
A.
B.
C.
D.
Cho hình (H) là hình phẳng giới hạn bởi parabol , đường cong và trục hoành (phần tô đậm trong hình vẽ). Tính diện tích S của hình (H)
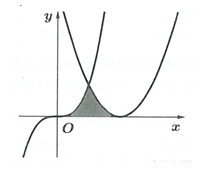
A.
B.
C.
D.
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) và đường thẳng d tương ứng có phương trình là và . Biết đường thẳng d cắt mặt phẳng (P) tại điểm M. Gọi N là điểm thuộc d sao cho , gọi K là hình chiếu vuông góc của điểm N trên mặt phẳng (P). Tính độ dài đoạn MK.
A.
B.
C.
D.
Với mức tiêu thụ thức ăn của trang trại A không đổi như dự định thì lượng thức ăn dự trù sẽ đủ dùng cho 100 ngày. Nhưng thực tế, mức tiêu thụ thức ăn tăng thêm 4% mỗi ngày (ngày sau tăng 4% so với ngày trước đó). Hỏi thực tế lượng thức ăn dự trữ đó chỉ đủ dùng cho bao nhiêu ngày?
A. 40
B. 42
C. 41
D. 43
Xét hai số phức thay đổi thõa mãn . Gọi A, B lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức . Gía trị của AB là
A. 110
B. 116
C. 112
D. 114
Phương trình có 2 nghiệm phân biệt khi và chỉ khi là phân số tối giản. Giá trị của biểu thức (b-a) bằng
A. -2
B. -1
C. 1
D. 2
Cho hàm số f(x) xác định trên khoảng thõa mãn . Tính giá trị của biểu thức
A. -2
B. 3
C. 2
D. -3
Cho hàm số liên tục trên thõa mãn . Khi đó tích phân bằng
A.
B.
C. -1
D. 1
Cho tứ diện đều S.ABC. Gọi I là trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng song song với (SIC). Thiết diện tạo bởi và tứ diện S.ABC là:
A. hình bình hành.
B. tam giác cân tại M.
C. tam giác đều.
D. hình thoi.
Cho . Gía trị của biểu thức bằng
A. S = -1
B.
C. S = 1
D. S = 0
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;0;-1) và mặt phẳng . Gọi (S) là mặt cầu có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho diện tích tam giác OIA bằng . Tính bán kính R của mặt cầu (S)
A. R = 3
B. R = 9
C. R = 1
D. R = 5
Cho dãy số thõa mãn và với mọi . Tìm
A. e
B.
C.
D.
Cho hàm số Tập hợp tất cả các giá trị m để đồ thị hàm số có năm cực trị là
A.
B.
C.
D.
Trong năm đầu tiên đi làm, anh A được nhận lương là 10 triệu đồng mỗi tháng. Cứ hết một năm, anh A lại được tăng lương, mỗi tháng năm sau tăng 12% so với mỗi tháng năm trước. Mỗi khi lĩnh lương, anh A đều phải cất đi phần lương tăng so với năm ngay trước để tiết kiệm mua ô tô. Hỏi sau ít nhất bao nhiêu năm thì anh A mua được ô tô giá 500 triệu, biết rằng anh A được gia đình hỗ trợ 32% giá trị chiếc xe?
A. 11
B. 12
C. 13
D. 10
Cho khối trụ tam giác có đáy là tam giác vuông cân với cạnh huyền . Mặt phẳng (AA'B) vuông góc với mặt phẳng (ABC), , góc A'AB nhọn và mặt phẳng (A'AC) tạo với (ABC) một góc . Thể tích khối lăng trụ bằng
A.
B.
C.
D.
Cho số phức z thõa mãn . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức . Tính
A. 1236
B. 1258
C. 1256
D. 1233
Cho tứ diện ABCD có CD = 3. Hai tam giác ACD, BCD có diện tích lần lượt là 15 và 10. Biết thể tích của tứ diện ABCD bằng 20. Tính côtang của góc giữa hai mặt phẳng (ACD) và (BCD).
A.
B.
C.
D.
Trong không gian với hệ tọa độ Oxyz, cho ba điểm với . Biết rằng (ABC) đi qua điểm và tiếp xúc với mặt cầu . Tính
A. 14
B.
C. 7
D.
Cho số phức z thõa mãn . Tìm giá trị lớn nhất của biểu thức
A. 8
B. 20
C.
D.
Trong mặt phẳng (P) cho tam giác OAB cân tại O, . Trên đường thẳng vuông góc với mặt phẳng (P) tại O lấy hai điểm C, D nằm về hai phía của mặt phẳng (P) sao cho tam giác ABC vuông tại C và tam giác ABD đều. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD.
A.
B
C.
D.
Biết với a, b, c là các số nguyên tố và e là cơ số của logarit tự nhiên. Tính .
A. S = 10
B. S = 0
C. S = 5
D. S = 9
Gọi S là tập hợp tất cả các số tự nhiên gồm 9 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số trong tập S. Tính xác suất để số được chọn có đúng 4 chữ số lẻ sao cho số 0 luôn đứng giữa hai chữ số lẻ
A.
B.
C.
D.
Trong không gian Oxyz, cho mặt cầu và đường thẳng . Điểm M(a;b;c)(với a < 0) trên đường thẳng d sao cho từ M kẻ được ba tiếp tuyến MA, MB, MC đến mặt cầu (S) ( A, B, C là các tiếp điểm) thõa mãn các góc . Tính abc bằng
A. 4
B.
C. -2
D. 2
Cho hàm số f(x). Biết hàm số có đồ thị như hình bên. Trên đoạn [-4;3], hàm số đạt giá trị nhỏ nhất tại điểm

A.
B.
C.
D.
Cho hai số thực x, y thõa mãn . Tìm giá trị lớn nhất của biểu thức
A. P = 10
B. P = 4
C. P = 6
D. P = 8
Cho hai số thực dương x, y thõa mãn điều kiện . Tìm giá trị nhỏ nhất của
A.
B.
C.
D.
Cho hàm số liên tục trên R và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm thuộc khoảng
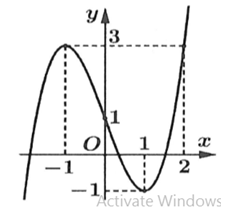
A. 2
B. 3
C. 4
D. 5
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng , đường thẳng và điểm A(1;3;1) thuộc mặt phẳng (P). Gọi là đường thẳng đi qua A, nằm trong mặt phẳng (P) và cách d một khoảng cách lớn nhất. Gọi là một vecto chỉ phương của đường thẳng . Tính b+c
A.
B.
C.
D.
Cho hàm số y = f(x) có đạo hàm trên R và đồ thị (C). Tiếp tuyến của đồ thị (C) tại điểm (2;m) có phương trình là . Tiếp tuyến của các đồ thị hàm số và tại điểm có hoành độ bằng 2 có phương trình lần lượt là . Tính giá trị của biểu thức
A. S = -26
B. S = 176
C. S = 178
D. S = 174


