Quiz

299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P8)

Admin40 câu hỏiToánLớp 11

40 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Xếp 4 người đàn ông, 2 người đàn bà và một đứa trẻ được xếp ngồi vào 7 chiếc ghế đặt quanh một bàn tròn. Xác suất để xếp đứa trẻ ngồi giữa hai người đàn ông là

$A . \frac{1}{15}$

$B . \frac{1}{5}$

$C . \frac{2}{15}$

$D . \frac{2}{5}$

2. Nhiều lựa chọn

Gọi S là tập hợp các số tự nhiên gồm 9 chữ số được lập từ X = {6;7;8}, trong đó chữ số 6 xuất hiện 2 lần; chữ số 7 xuất hiện 3 lần; chữ số 8 xuất hiện 4 lần. Chọn ngẫu nhiên một số từ tập S. Xác suất để số được chọn là số không có chữ số 7 đứng giữa hai chữ số 6 là

$A . \frac{2}{5}$

$B . \frac{11}{12}$

$C . \frac{4}{5}$

$D . \frac{55}{432}$

3. Nhiều lựa chọn

Cho một bảng ô vuông 3x3

Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên (mỗi ô chỉ điền một số). Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của A bằng:

A. P(A) = $\frac{1}{3}$

B. P(A) = $\frac{5}{7}$

C. P(A) = $\frac{1}{56}$

D. P(A) = $\frac{10}{21}$

4. Nhiều lựa chọn

Trong kỳ thi Chọn học sinh giỏi tỉnh có em dự thi, có 105 em tham gia buổi gặp mặt trước kỳ thi. Biết các em đó có số thứ tự trong danh sách lập thành một cấp số cộng. Các em ngồi ngẫu nhiên vào hai dãy bàn đối diện nhau, mỗi dãy có 5 ghế và mỗi ghế chỉ ngồi được 1 học sinh. Tính xác suất để tổng các số thứ tự của hai em ngồi đối diện nhau là bằng nhau.

$A . \frac{1}{954}$

$B . \frac{1}{945}$

$C . \frac{1}{126}$

$D . \frac{1}{252}$

5. Nhiều lựa chọn

Trong mặt phẳng, cho hai tia Ox và Oy vuông góc với nhau tại gốc O. Trên tia Ox lấy 10 điểm $A_{1}, A_{2}, . . ., A_{10}$ và trên tia Oy lấy 10 điểm $B_{1}, B_{2}, . . . ., B_{10}$ thỏa mãn $O A_{1} = A_{1} A_{2} = . . . = A_{9} A_{10} = O B_{1} = B_{1} B_{2} = . . . . = B_{9} B_{10} = 1$ (đvd). Chọn ra ngẫu nhiên một tam giác có đỉnh nằm trong 20 điểm $A_{1}, A_{2}, . . . ., A_{10}, B_{1}, B_{2}, . . ., B_{10}$ . Xác suất để tam giác chọn được có đường tròn ngoại tiếp tiếp xúc với một trong hai trục Ox hoặc Oy là

$A . \frac{1}{228}$

$B . \frac{2}{225}$

$C . \frac{1}{225}$

$D . \frac{1}{114}$

6. Nhiều lựa chọn

Cho tập A = {0;1;2;3;4;5;6}. Xác suất để lập được số tự nhiên gồm 5 chữ số khác nhau lấy từ các phần tử của tập A sao cho số đó chia hết cho 1,2,3 và các chữ số 1,2,3 luôn có mặt cạnh nhau là

$A . \frac{23}{31}$

$B . \frac{35}{120}$

$C . \frac{15}{313}$

$D . \frac{11}{160}$

7. Nhiều lựa chọn

Cho tập S = {1;2;3;...;19;20} gồm 20 số tự nhiên từ 1 đến 20. Lấy ngẫu nhiên ba số thuộc S. Xác suất để ba số lấy được lập thành một cấp số cộng là

$A . \frac{7}{38}$

$B . \frac{5}{38}$

$C . \frac{3}{38}$

$D . \frac{1}{114}$

8. Nhiều lựa chọn

Từ tập hợp tất cả các số tự nhiên có năm chữ số mà các chữ số đều khác 0, lấy ngẫu nhiên một số. Xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là:

$A . \frac{504}{59049}$

$B . \frac{7560}{59049}$

$C . \frac{1260}{59049}$

$D . \frac{12600}{59049}$

9. Nhiều lựa chọn

Có 3 quả cầu màu vàng, 3 quả cầu màu xanh (các quả cầu cùng màu thì giống nhau) bỏ vào hai cái hộp khác nhau, mỗi hộp quả cầu. Tính xác suất để các quả cầu cùng màu thì vào chung một hộp.

$A . \frac{1}{3}$

$B . \frac{1}{120}$

$C . \frac{1}{20}$

$D . \frac{1}{2}$

10. Nhiều lựa chọn

Có 15 cuốn sách gồm 4 cuốn sách Toán, 5 cuốn sách Lý và 6 cuốn sách Hóa. Các cuốn sách đôi một khác nhau. Thầy giáo chọn ngẫu nhiên 8 cuốn sách để làm phần thưởng cho một học sinh. Tính xác suất để số cuốn sách còn lại của thầy còn đủ 3 môn

$A . \frac{54}{175}$

$B . \frac{2072}{2145}$

$C . \frac{661}{715}$

$D . \frac{73}{2145}$

11. Nhiều lựa chọn

Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng $\bar{a b c d}$ , trong đó 1 $\leq$ a $\leq$ b $\leq$ c $\leq$ d $\leq$ 9

A. 0,014

B. 0,0495

C. 0,079

D. 0,055

12. Nhiều lựa chọn

Xếp ngẫu nhiên 2 quả cầu xanh, 2 quả cầu đỏ, 2 quả cầu trắng (các quả cầu này đôi một khác nhau) thành một hàng ngang. Tính xác suất để 2 quả cầu màu trắng không xếp cạnh nhau?

A. P = $\frac{2}{3}$

B. P = $\frac{1}{3}$

C. P = $\frac{5}{6}$

D. P = $\frac{1}{2}$

13. Nhiều lựa chọn

Lập một số tự nhiên có 4 chữ số. Tính xác suất để số đó có chữ số đứng trước không nhỏ hơn chữ số đứng sau.

$A . \frac{14}{25}$

$B . \frac{143}{1800}$

$C . \frac{119}{1500}$

$D . \frac{11}{200}$

14. Nhiều lựa chọn

Giải bóng chuyền quốc tế VTV Cup có 8 đội tham gia, trong đó có hai đội Việt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia thành hai bảng đấu, mỗi bảng 4 đội. Xác suất để hai đội của Việt Nam nằm ở hai bảng khác nhau bằng

$A . \frac{2}{7}$

$B . \frac{5}{7}$

$C . \frac{3}{7}$

$D . \frac{4}{7}$

15. Nhiều lựa chọn

Giải bóng chuyền quốc tế VTV Cup có 12 đội tham gia, trong đó có 3 đội Việt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia thành 3 bảng đấu, mỗi bảng 4 đội. Tính xác suất để 3 đội của Việt Nam cùng nằm ở một bảng đấu.

$A . \frac{3}{55}$

$B . \frac{1}{330}$

$C . \frac{1}{110}$

$D . \frac{6}{55}$

16. Nhiều lựa chọn

Cho tập X = {1;2;3;....;8}. Lập từ X số tự nhiên có 8 chữ số đôi một khác nhau. Xác suất để lập được số chia hết cho 1111 là

$A . \frac{C_{8}^{2} C_{6}^{2} C_{4}^{2}}{8!}$

$B . \frac{4! . 4!}{8!}$

$C . \frac{384}{8!}$

$D . \frac{A_{8}^{2} A_{6}^{2} A_{4}^{2}}{8!}$

17. Nhiều lựa chọn

Cho S là tập tất cả các số tự nhiên có 7 chữ số, lấy ngẫu nhiên một số từ tập S. Xác suất để số lấy được có chữ số tận cùng bằng 3 và chia hết cho 7 có kết quả gần nhất với số nào trong các số sau

A. 0,014

B. 0,012.

C. 0,128.

D. 0,035.

18. Nhiều lựa chọn

A. 0,014

B. 0,012.

C. 0,128.

D. 0,035.

19. Nhiều lựa chọn

Hai bạn Công và Thành cùng viết ngẫu nhiên ra một số tự nhiên gồm 2 chữ số phân biệt. Xác suất để hai số được viết ra có ít nhất một chữ số chung bằng

$A . \frac{145}{729}$

$B . \frac{448}{729}$

$C . \frac{281}{729}$

$D . \frac{154}{729}$

20. Nhiều lựa chọn

Gọi S là tập tất cả các số tự nhiên có 4 chữ số đôi một khác nhau được chọn từ các chữ số 1,2,3,4,5,6,7,8,9. Lấy ngẫu nhiên một số thuộc S. Tính xác suất để lấy được một số chia hết cho 11 và tổng 4 chữ số của nó cũng chia hết cho 11.

$A . P = \frac{1}{63}$

$B . P = \frac{1}{126}$

$C . P = \frac{2}{63}$

$D . P = \frac{8}{21}$

21. Nhiều lựa chọn

Gọi A là tập các số tự nhiên có 3 chữ số đôi một khác nhau. Lấy ngẫu nhiên ra từ A hai số. Tính xác suất để lấy được hai số mà các chữ số có mặt ở hai số đó giống nhau.

$A . \frac{41}{5823}$

$B . \frac{35}{5823}$

$C . \frac{41}{7190}$

$D . \frac{14}{1941}$

22. Nhiều lựa chọn

Cho một quân cờ đứng ở vị trí trung tâm của một bàn cờ 9x9 (xem hình vẽ). Biết rằng, mỗi lần di chuyển, quân cờ chỉ di chuyển sang ô có cùng một cạnh với ô đang đứng. Tính xác suất để sau bốn lần di chuyển, quân cờ không trở về đúng vị trí ban đầu.

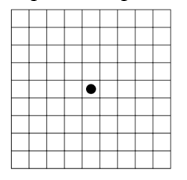
$A . \frac{55}{64}$

$B . \frac{1}{3}$

$C . \frac{7}{8}$

$D . \frac{3}{8}$

23. Nhiều lựa chọn

Cho A là tập tất cả các số tự nhiên có 5 chữ số. Chọn ngẫu nhiên một số từ tập A, tính xác suất để chọn được một số chia hết cho 7 và chữ số hàng đơn vị là chữ số 1.

$A . \frac{643}{45000}$

$B . \frac{1285}{90000}$

$C . \frac{107}{7500}$

$D . \frac{143}{10000}$

24. Nhiều lựa chọn

Cho A là tập tất cả các số tự nhiên có 5 chữ số phân biệt. Chọn ngẫu nhiên một số từ tập tính xác suất để chọn được một số chia hết cho 7 và chữ số hàng đơn vị bằng 1.

$A . \frac{11}{567}$

$B . \frac{643}{45000}$

$C . \frac{79}{4536}$

$D . \frac{643}{13608}$

25. Nhiều lựa chọn

Cho A là tập tất cả các số tự nhiên có 4 chữ số phân biệt được lập từ tập {1;2;3;4;5;6;7;8;9}. Chọn ngẫu nhiên một số từ tập A. Xác suất để chọn được một số chia hết cho 11 và tổng bốn chữ số của nó chia hết cho 11 bằng

$A . \frac{1}{63}$

$B . \frac{8}{21}$

$C . \frac{1}{84}$

$D . \frac{1}{42}$

26. Nhiều lựa chọn

Cho đa giác 30 đỉnh nội tiếp đường tròn, gọi (S) là tập hợp các đường thẳng đi qua hai trong số 30 đỉnh đã cho. Chọn 2 đường thẳng bất kỳ thuộc tập (S). Tính xác suất để chọn được 2 đường thẳng mà giao điểm của chúng nằm bên trong đường tròn.

$A . \frac{7}{25}$

$B . \frac{2}{5}$

$C . \frac{5}{14}$

$D . \frac{9}{31}$

27. Nhiều lựa chọn

$A . \frac{7}{25}$

$B . \frac{2}{5}$

$C . \frac{5}{21}$

$D . \frac{9}{31}$

28. Nhiều lựa chọn

Cho một đa giác đều có 20 đỉnh nội tiếp trong đường tròn (C). Lấy ngẫu nhiên hai đường chéo trong số các đường chéo của đa giác. Tính xác suất để lấy được hai đường chéo cắt nhau và giao điểm của hai đường chéo trong đường tròn?

$A . \frac{17}{63}$

$B . \frac{57}{169}$

$C . \frac{19}{63}$

$D . \frac{17}{169}$

29. Nhiều lựa chọn

Nhằm chào mừng ngày thành lập Đoàn TNCS Hồ Chí Minh, Đoàn trường THPT chuyên Lương Thế Vinh đã tổ chức giải bóng đá nam. Có 16 đội đăng kí tham dự trong đó có 3 đội: 10 Toán, 11 Toán, 12 Toán. Ban tổ chức cho bốc thăm ngẫu nhiên để chia đều 16 đội vào 4 bảng để đá vòng loại. Tính xác suất để 3 đội của 3 lớp Toán nằm ở bảng khác nhau.

$A . \frac{53}{56}$

$B . \frac{19}{28}$

$C . \frac{16}{35}$

$D . \frac{3}{56}$

30. Nhiều lựa chọn

Tung đồng thời 2 con súc sắc cân đối đồng chất. Gọi m là tích của số chấm trên hai con súc sắc trong mỗi lần tung. Tính xác suất để phương trình $\frac{1}{2} x^{2} + 6 x + m = 0$ có hai nghiệm phân biệt.

$A . \frac{28}{36}$

$B . \frac{24}{36}$

$C . \frac{17}{36}$

$D . \frac{26}{36}$

31. Nhiều lựa chọn

Gọi X là tập hợp các số tự nhiên có 6 chữ số đôi một khác nhau. Lấy ngẫu nhiên một số thuộc tập X. Xác suất để số lấy được luôn chứa đúng ba số thuộc tập Y = {1;2;3;4;5} và 3 số đứng cạnh nhau, số chẵn đứng giữa hai số lẻ.

$A . \frac{37}{63}$

$B . \frac{25}{189}$

$C . \frac{25}{378}$

$D . \frac{17}{945}$

32. Nhiều lựa chọn

Trong một buổi dạ hội có 10 thành viên nam và 12 thành viên nữ, trong đó có 2 cặp vợ chồng. Ban tổ chức muốn chọn ra 7 đôi, mỗi đôi gồm 1 nam và 1 nữ để tham gia trò chơi. Tính xác suất để trong 7 đôi đó, có đúng một đôi là cặp vợ chồng. Biết rằng trong trò chơi, người vợ có thể ghép đôi với một người khác chồng mình và người chồng có thể ghép đôi với một người khác vợ mình

$A . \frac{7}{160}$

$B . \frac{217}{1980}$

$C . \frac{217}{3960}$

$D . \frac{7}{120}$

33. Nhiều lựa chọn

Chọn ngẫn nhiên ba số tự nhiên trong các số từ 101 đến 200. Tính xác suất để ba số đó lập thành một cấp số cộng có công sai dương.

$A . \frac{3}{100}$

$B . \frac{2}{33}$

$C . \frac{1}{66}$

$D . \frac{1}{33}$

34. Nhiều lựa chọn

Một nhóm học sinh gồm bốn bạn nam trong đó có bạn Quân và bốn bạn nữ trong đó có bạn Lan. Xếp ngẫu nhiên bốn bạn trên thành một hàng dọc. Xác suất để xếp được hàng dọc thỏa mãn các điều kiện: đầu hàng và cuối hàng đều là nam và giữa hai bạn nam gần nhau có ít nhất một bạn nữ, đồng thời bạn Quân và bạn Lan không đứng cạnh nhau bằng

$A . \frac{3}{112}$

$B . \frac{3}{80}$

$C . \frac{9}{280}$

$D . \frac{39}{1120}$

35. Nhiều lựa chọn

Cho tập hợp (S). Hai bạn A, B mỗi bạn chọn ngẫu nhiên một tập con của (S). Xác suất để tập con của A và B chọn được có đúng 2 phần tử chung gần nhất với kết quả nào dưới đây?

A. 15,08%

B. 29,66%

C. 30,16%

D. 14,83%

36. Nhiều lựa chọn

A. 0,014.

B. 0,012.

C. 0,128.

D. 0,035.

37. Nhiều lựa chọn

Cho một đa giác đều 48 đỉnh. Lấy ngẫu nhiên 3 đỉnh của đa giác. Tính xác suất để tam giác tạo thành từ ba đỉnh đó là một tam giác nhọn.

$A . \frac{33}{47}$

$B . \frac{93}{94}$

$C . \frac{11}{47}$

$D . \frac{22}{47}$

38. Nhiều lựa chọn

Trong chương trình giao lưu gồm có 15 người ngồi vào 15 ghế theo một hàng ngang. Giả sử người dẫn chương trình chọn ngẫu nhiên 3 người trong 15 người để giao lưu với khán giả. Xác suất để trong 3 người được chọn đó không có 2 người ngồi kề nhau là

$A . \frac{2}{5}$

$B . \frac{13}{35}$

$C . \frac{22}{35}$

$D . \frac{3}{5}$

39. Nhiều lựa chọn

Có hai dãy ghế đối diện nhau, mỗi dãy có 3 ghế. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3 nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng:

$A . \frac{2}{5}$

$B . \frac{1}{10}$

$C . \frac{3}{5}$

$D . \frac{1}{20}$

40. Nhiều lựa chọn

Gọi S là tập hợp các số tự nhiên có chín chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc tập S. Xác suất để số được chọn chia hết cho 3 là

$A . \frac{11}{27}$

$B . \frac{12}{27}$

$C . \frac{21}{32}$

$D . \frac{23}{32}$

Gợi ý cho bạn

QuizToán - Tốt nghiệp THPT

Trắc nghiệm củng cố

2 câu hỏi3 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi5 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi28 lượt thi

QuizToán - Lớp 12

10 bài tập Xác định các yếu tố cơ bản của đường thẳng trong không gian có lời giải

10 câu hỏi16 lượt thi

QuizToán - Lớp 12

10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải

10 câu hỏi14 lượt thi

QuizToán - Lớp 12

10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Khoảng cách từ một điểm đến một mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình mặt phẳng đi qua 1 điểm kèm điều kiện song song với mặt phẳng khác có lời giải

10 câu hỏi13 lượt thi

Facebook Youtube