Quiz

27 câu Trắc nghiệm Toán 9 Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông có đáp án (Phần 2)

Admin27 câu hỏiToánLớp 9

Bắt đầu ngay

27 CÂU HỎI

Hiển thị đáp án

1. Nhiều lựa chọn

Cho tam giác MNP vuông tại N. Hệ thức nào sau đây là đúng?

A. MN = MP. sin P

B. MN = MP. cos P

C. MN = MP. tan P

D. MN = MP. cot P

2. Nhiều lựa chọn

Cho tam giác MNP vuông tại N. Hệ thức nào sau đây là đúng?

Cho tam giác MNP vuông tại N. Hệ thức nào sau đây là đúng A. NP = MP. sin P B. NP = MN. cot P (ảnh 1)

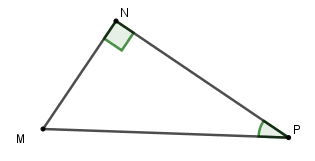
A. NP = MP. sin P

B. NP = MN. cot P

C. NP = MN. tan P

D. NP = MP. cot P

3. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Chọn khẳng định sai?

A. b = a.sin B = a.cos C

B. a = c.tan B = c.cot C

C. $a^{2} = b^{2} + c^{2}$

D. c = a.sin C = a.cos B

4. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có BC = a, AC = b, $\hat{A B C} = 50^{0}$ . Chọn khẳng định đúng.

A. b = c.sin $50^{0}$ .

B. b = a.tan $50^{0}$ .

C. b = c.cot $50^{0}$ .

D. c = b.cot $50^{0}$ .

5. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có AC = 10cm, $\hat{C} = 30^{0}$ . Tính AB, BC

A. AB = $\frac{5 \sqrt{3}}{3}$ ; BC = $\frac{20 \sqrt{3}}{3}$

B. AB = $\frac{10 \sqrt{3}}{3}$ ; BC = $\frac{14 \sqrt{3}}{3}$

C. AB = $\frac{10 \sqrt{3}}{3}$ ; BC = 20 $\sqrt{3}$

D. AB = $\frac{10 \sqrt{3}}{3}$ ; BC = $\frac{20 \sqrt{3}}{3}$

6. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có AC = 20cm, $\hat{C} = 60^{0}$ . Tính AB, BC

A. AB = 20 $\sqrt{3}$ ; BC = 40

B. AB = 20 $\sqrt{3}$ ; BC = 40 $\sqrt{3}$

C. AB = 20; BC = 40

D. AB = 20; BC = 20 $\sqrt{3}$

7. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có BC = 12cm, $\hat{B} = 40^{0}$ . Tính AC; $\hat{C}$ (làm tròn đến chữ số thập phân thứ hai)

A. $A C \approx 7, 71; \hat{C} = 40^{0}$

B. $A C \approx 7, 72; \hat{C} = 50^{0}$

C. $A C \approx 7, 71; \hat{C} = 50^{0}$

D. $A C \approx 7, 73; \hat{C} = 50^{0}$

8. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có BC = 15cm, $\hat{B} = 55^{0}$ . Tính AC; $\hat{C}$ (làm tròn đến chữ số thập phân thứ hai)

A. $A C \approx 12, 29; \hat{C} = 45^{0}$

B. $A C \approx 12, 29; \hat{C} = 35^{0}$

C. $A C \approx 12, 2; \hat{C} = 35^{0}$

D. $A C \approx 12, 92; \hat{C} = 40^{0}$

9. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có BC = 15cm, AB = 12cm. Tính AC, $\hat{B}$

A. AC = 8 (cm); $\hat{B} \approx 36^{0} 52'$

B. AC = 9 (cm); $\hat{B} \approx 36^{0} 52'$

C. AC = 9 (cm); $\hat{B} \approx 37^{0} 52'$

D. AC = 9 (cm); $\hat{B} \approx 36^{0} 55'$

10. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có AC = 7cm, AB = 5cm. Tính BC; $\hat{C}$

A. $B C = \sqrt{74} (c m); \hat{C} \approx 35^{0} 32'$

B. $B C = \sqrt{74} (c m); \hat{C} \approx 36^{0} 32'$

C. $B C = \sqrt{74} (c m); \hat{C} \approx 35^{0} 33'$

D. $B C = \sqrt{74} (c m); \hat{B} \approx 35^{0} 32'$

11. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có BC = 26cm, AB = 10cm. Tính AC, $\hat{B}$ (làm tròn đến độ)

A. AC = 22; $\hat{B} \approx 67^{0}$

B. AC = 24; $\hat{B} \approx 66^{0}$

C. AC = 24; $\hat{B} \approx 67^{0}$

D. AC = 24; $\hat{B} \approx 68^{0}$

12. Nhiều lựa chọn

Cho tam giác ABC có AB = 16, AC = 14 và $\hat{B} = 60^{0}$ . Tính BC

A. BC = 10

B. BC = 11

C. BC = 9

D. BC = 12

13. Nhiều lựa chọn

Cho tam giác ABC có AB = 12, AC = 15 và $\hat{B} = 60^{0}$ . Tính BC

A. BC = $3 \sqrt{3} + 6$

B. BC = $3 \sqrt{13} + 6$

C. BC = 9

D. BC = 6

14. Nhiều lựa chọn

Cho tam giác ABC có $\hat{B} = 60^{0}$ , $\hat{C} = 50^{0}$ , AC = 3,5cm. Diện tích tam giác ABC gần nhất với giá trị nào dưới đây?

A. 4

B. 5

C. 7

D.8

15. Nhiều lựa chọn

Cho tam giác ABC có $\hat{B} = 70^{0}$ , $\hat{C} = 35^{0}$ , AC = 4,5cm. Diện tích tam giác ABC gần nhất với giá trị nào dưới đây? (làm tròn đến chữ số thập phân thứ hai)

A. 4

B. 5

C. 6

D. 8

16. Nhiều lựa chọn

Tứ giác ABCD có $\hat{A} = \hat{D} = 90^{0}$ , $\hat{C} = 40^{0}$ , AB = 4cm, AD = 3cm. Tính diện tích tứ giác ABCD (làm tròn đến chữ số thập phân thứ hai).

A. 17,36 $c m^{2}$

B. 17,4 $c m^{2}$

C. 17,58 $c m^{2}$

D. 17,54 $c m^{2}$ .

17. Nhiều lựa chọn

Tứ giác ABCD có $\hat{A} = \hat{D} = 90^{0}$ , $\hat{C} = 45^{0}$ , AB = 6cm, AD = 8cm. Tính diện tích tứ giác ABCD

A. 60 $c m^{2}$ .

B. 80 $c m^{2}$ .

C. 40 $c m^{2}$ .

D. 160 $c m^{2}$ .

18. Nhiều lựa chọn

Cho tam giác ABC cân tại A, $\hat{B} = 65^{0}$ , đường cao CH = 3,6. Hãy giải tam giác ABC

A. $\hat{A} = 50^{0}$ ; $\hat{C} = 65^{0}$ ; AB = AC = 5,6; BC = 8,52

B. $\hat{A} = 50^{0}$ ; $\hat{C} = 65^{0}$ ; AB = AC = 5,6; BC = 4,42

C. $\hat{A} = 50^{0}$ ; $\hat{C} = 65^{0}$ ; AB = AC = 4,7; BC = 4,24

D. $\hat{A} = 50^{0}$ ; $\hat{C} = 65^{0}$ ; AB = AC = 4,7; BC = 3,97

19. Nhiều lựa chọn

Cho tam giác ABC vuông tại A, đường cao AH, biết HB = 9; HC = 16. Tính góc B và góc C.

A. $\hat{B} = 53^{0} 8'$ ; $\hat{C} = 36^{0} 52'$

B. $\hat{B} = 36^{0} 52'$ ; $\hat{C} = 53^{0} 8'$

C. $\hat{B} = 48^{0} 35'$ ; $\hat{C} = 41^{0} 25'$

D. $\hat{B} = 41^{0} 25'$ ; $\hat{C} = 48^{0} 35'$

20. Nhiều lựa chọn

Một tam giác cân có đường cao ứng với đáy đúng bằng độ dài đáy. Tính các góc của tam giác đó.

A. $\hat{A} = 45^{0}$ ; $\hat{B} = \hat{C} = 67^{0} 30'$

B. $\hat{A} = 30^{0}$ ; $\hat{B} = \hat{C} = 75^{0}$

C. $\hat{A} = 48^{0} 6'$ ; $\hat{B} = \hat{C} = 65^{0} 57'$

D. $\hat{A} = 53^{0} 8'$ ; $\hat{B} = \hat{C} = 63^{0} 26'$

21. Nhiều lựa chọn

Cho tam giác ABC vuông cân tại A (AB = AC = a). Phân giác của góc B cắt AC tại D. Tính DA; DC theo a

A. $A D = a . \cos 22, 5^{0}$ ; $D C = a - a . \cos 22, 5^{0}$ .

B. $A D = a . \sin 22, 5^{0}$ ; $D C = a - a . \sin 22, 5^{0}$ .

C. $A D = a . \tan 22, 5^{0}$ ; $D C = a - a . \tan 22, 5^{0}$ .

D. $A D = a . co t 22, 5^{0}$ ; $D C = a - a . c o t 22, 5^{0}$ .

22. Nhiều lựa chọn

Cho tam giác ABC vuông tại A có đường cao AH (H thuộc BC). Biết $\hat{A C B} = 60^{0}$ , CH = a. Tính độ dài AB và AC theo a

A. $\{\begin{cases} A B = 2 \sqrt{3} a \\ A C = 2 a \end{cases}$

B. $\{\begin{cases} A B = \sqrt{3} a \\ A C = \frac{1}{2} a \end{cases}$

C. $\{\begin{cases} A B = a \\ A C = 3 a \end{cases}$

D. $\{\begin{cases} A B = \sqrt{3} a \\ A C = a \end{cases}$

23. Nhiều lựa chọn

Cho hình thang ABCD vuông tại A và D; $\hat{C} = 50^{0}$ . Biết AB = 2; AD = 1,2. Tính diện tích hình thang ABCD

A. $S_{A B C D}$ = 2 (đvdt)

B. $S_{A B C D}$ = 3 (đvdt)

C. $S_{A B C D}$ = 4 (đvdt)

D. $S_{A B C D}$ = $\frac{5}{2}$ (đvdt)

24. Nhiều lựa chọn

Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 3cm, AC = 4cm. Tính độ dài đường cao AH, tính $c o s \hat{A C B}$ và chu vi tam giác ABH.

A. AH = 2,8 cm; $c o s \hat{A C B} = \frac{3}{5}$

B. AH = 2,4 cm; $c o s \hat{A C B} = \frac{4}{5}$

C. AH = 2,5 cm; $c o s \hat{A C B} = \frac{3}{4}$

D. AH = 1,8 cm; $c o s \hat{A C B} = \frac{2}{3}$

25. Nhiều lựa chọn

Cho tam giác ABC vuông tại A; BC = a không đổi, $\hat{C} = α$ $(0^{0} < α < 90^{0})$

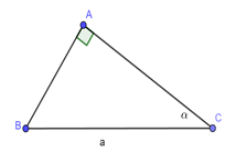
Cho tam giác ABC vuông tại A; BC = a không đổi, góc C= anpha( 0 độ < anpha < 90 độ) (ảnh 1)

Lập công thức để tính diện tích tam giác ABC theo a và

A. $\frac{1}{2} a^{2} \sin α . \cos α$

B. $a^{2} \sin α . \cos α$

C. $2 a^{2} \sin α . \cos α$

D. $3 a^{2} \sin α . \cos α$

26. Nhiều lựa chọn

Cho tam giác ABC vuông tại A; BC = a không đổi, $\hat{C} = α$ $(0^{0} < α < 90^{0})$

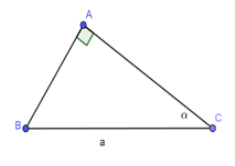
Cho tam giác ABC vuông tại A; BC = a không đổi, góc C= anpha ( 0 độ < anpha < 90 độ) (ảnh 1)

Tìm góc để diện tích tam giác ABC là lớn nhất. Tính giá trị lớn nhất ấy.

A. $α = 45^{0}$ ; $m a x_{S_{A B C}} = \frac{1}{2} a^{2}$ .

B. $α = 30^{0}$ ; $m a x_{S_{A B C}} = \frac{\sqrt{3}}{4} a^{2}$ .

C. $α = 60^{0}$ ; $m a x_{S_{A B C}} = \frac{\sqrt{3}}{4} a^{2}$ .

D. $α = 45^{0}$ ; $m a x_{S_{A B C}} = \frac{1}{4} a^{2}$ .

27. Nhiều lựa chọn

Cho tam giác DEF có DE = 7cm; $\hat{D} = 40^{0}$ ; $\hat{F} = 58^{0}$ . Kẻ đường cao EI của tam giác đó.

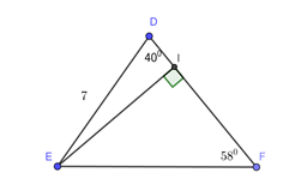
Cho tam giác DEF có DE = 7cm; góc D=40 độ; góc F=58 độ Kẻ đường cao EI của tam giác đó. (ảnh 1)

Hãy tính: (Kết quả làm tròn đến chữ số thập phân thứ 1). Đường cao EI:

A. EI = 4,5cm

B. EI = 5,4cm

C. EI = 5,9cm

D. EI = 5,6cm

Gợi ý cho bạn

QuizToán - Tốt nghiệp THPT

Trắc nghiệm củng cố

2 câu hỏi3 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi5 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình đường thẳng đi qua 1 điểm và có một vectơ chỉ phương có lời giải

11 câu hỏi28 lượt thi

QuizToán - Lớp 12

10 bài tập Xác định các yếu tố cơ bản của đường thẳng trong không gian có lời giải

10 câu hỏi16 lượt thi

QuizToán - Lớp 12

10 bài tập Vận dụng kiến thức phương trình mặt phẳng vào giải quyết bài toán liên quan đến thực tế có lời giải

10 câu hỏi14 lượt thi

QuizToán - Lớp 12

10 bài tập Vị trí tương đối giữa hai mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Khoảng cách từ một điểm đến một mặt phẳng có lời giải

10 câu hỏi13 lượt thi

QuizToán - Lớp 12

10 bài tập Viết phương trình mặt phẳng đi qua 1 điểm kèm điều kiện song song với mặt phẳng khác có lời giải

10 câu hỏi13 lượt thi

Facebook Youtube