30 câu hỏi
Hình bên là đồ thị của hàm số nào sau đây:
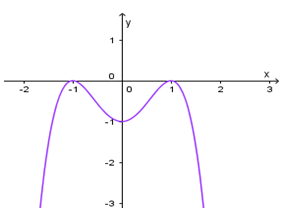
y = -x2 + 2x – 1
y = -x4 – 2x2 – 1
y = -x4 + x2 – 1
y = -x4 + 2x2 – 1
Đường cong hình bên dưới là đồ thị hàm số nào trong 4 hàm số sau:
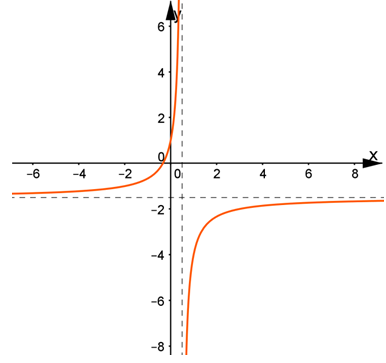
![]()
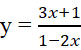
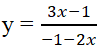
![]()
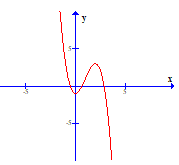
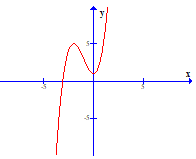
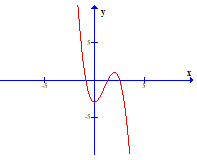
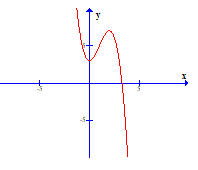
Hàm số y = -x3 + 3x2 – 1 là đồ thị nào sau đây
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên
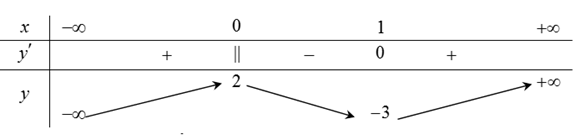
Khẳng định nào sau đây là khẳng định đúng
Hàm số có đúng một cực trị
Hàm số có giá trị cực tiểu bằng 2
Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3
Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

y = x4 – 2x2 – 1
y = -x4 + 2x2 – 1
y = x4 + 2x2 – 1
y = x4/2+ x2 – 1
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên:
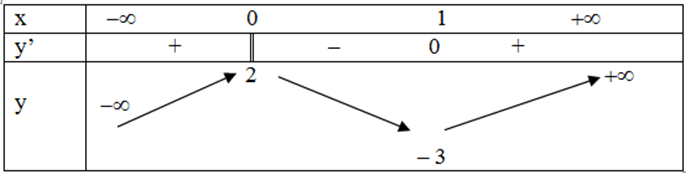
Khẳng định nào sau đây là khẳng định đúng?
Hàm số có đúng một cực trị
Hàm số có giá trị cực tiểu bằng 2
Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3
Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau:

Khẳng định nào sau đây đúng?
Hàm số có giá trị nhỏ nhất bằng 0 và giá trị lớn nhất bằng 2
Giá trị cực đại của hàm số bằng 5
Hàm số có đúng một điểm cực trị
Hàm số đạt cực tiểu tại x = 2 và x = 8
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên:
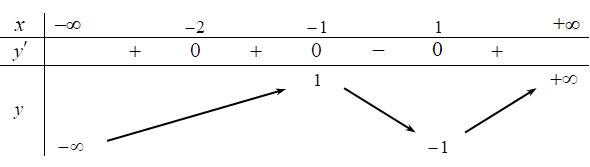
Mệnh đề nào dưới đây đúng?
Hàm số đồng biến trên khoảng (-∞;-1)
Đồ thị hàm số không có tiệm cận ngang
Hàm số đạt cực trị tại x = -2
Hàm số có giá trị lớn nhất bằng 1
Đồ thị ở hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?
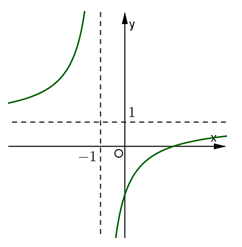
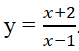
![]()
![]()
![]()
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
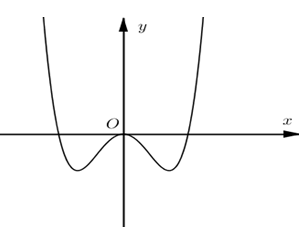
y = -x4 + 2x2
y = x4 + 2x2
y = -x4 – 2x2
y = x4 – 2x2
Đường cong hình bên là đồ thị của một hàm số nào trong bốn hàm số dưới đây
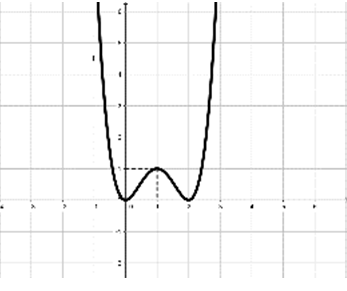
y = x4 – 4x3 + 4x2
y = x2 – 4x + 4
y = -x4 + 4x3 – 4x2
y = -x2 + 4x – 4
Cho hàm số y = f(x) xác định và liên tục trên R và có bảng biến thiên. Khẳng định sai?
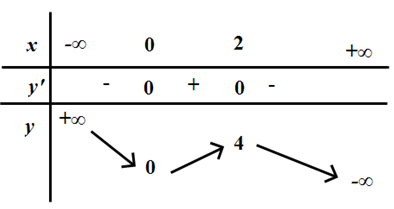
Hàm số có giá trị lớn nhất bằng 4
Hàm số đồng biến trên khoảng (0;2)
Hàm số đạt cực tiểu tại điểm x = 0
Hàm số đạt cực đại tại điểm x = 2
Cho hàm số y = f(x) xác định, liên tục trên R và có đồ thị là đường cong trong hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng?
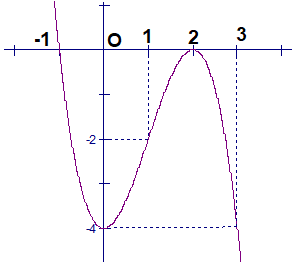
Hàm số đồng biến trên khoảng (-1;0)
Hàm số đồng biến trên khoảng (-4;2)
Hàm số nghịch biến trên khoảng (-1;0) ∪(2;3)
Hàm số nghịch biến trên khoảng (-4;1).
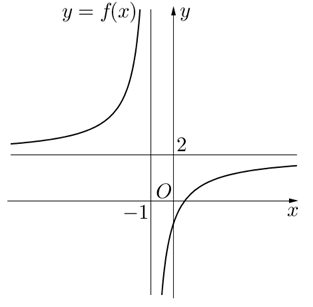
Hình bên là đồ thị của một trong bốn hàm số được cho trong các phương án A, B, C, D; hỏi đó là hàm nào?
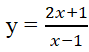
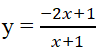
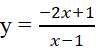
![]()
Đồ thị hình bên là của hàm số nào? Chọn một khẳng định ĐÚNG
y = x3 – 3x2 + 1
y = -x3/3 + x2 + 1
y = 2x3 – 6x2 + 1
y = -x3 – 3x2 + 1
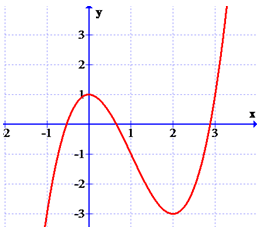
Tìm a, b để hàm số có đồ thị như hình vẽ bên
a = -1, b = -2
a = 1, b = -2
a = -2, b = 1
a = 2, b = 1
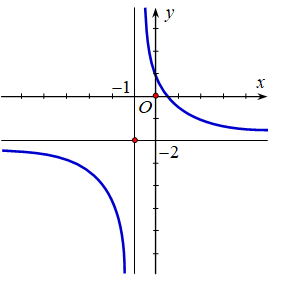
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ. Phát biểu nào sau đây là đúng?
Đồ thị hàm số có 2 điểm cực tiểu là (2;-1), (2;1) và 1 điểm cực đại là (0;1)
Đồ thị hàm số có 2 điểm cực đại là (-1;2), (1;2) và 1 điểm cực tiểu là (0;1)
Đồ thị hàm số có 1 điểm cực đại là (1;0) và 2 điểm cực tiểu là (-1;2), (1;2).
Đồ thị hàm số có 2 điểm cực đại là (2;-1), (2;1) và 1 điểm cực tiểu là (1;0)
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên.
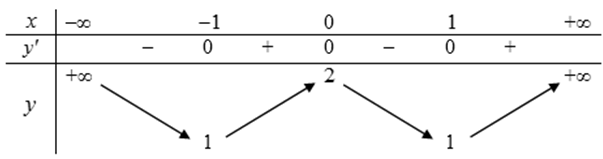
Hàm số đồng biến trên các khoảng (-1;0) và (1;+∞)
f (1) và f(-1) được gọi là giá trị cực tiểu của hàm số
x0 = 1 được gọi là điểm cực tiểu của hàm số
M(0;2) được gọi là điểm cực đại của hàm số
Số giao điểm của trục hoành và đồ thị hàm số y = -x4 + 2x2 + 3 là:
1
3
2
4
Tìm số giao điểm của đồ thị hàm số y = (x – 2)(x2 + x + 1) và trục hoành.
1
0
2
3
Tìm số giao điểm của đồ thị (C): y = x3 + x – 2 và đường thẳng y = x – 1
2
3
0
1
Tìm số giao điểm của đồ thị hàm số y = x4 – 2x2 và đồ thị hàm số y = x2 – 2
4
2.
3
1
Tìm số giao điểm của đồ thị hàm số y = và đường thẳng y = -x.
3
1
2.
0
Cho hàm số y = x4 – 2x2 – 1. Tìm số giao điểm của đồ thị hàm số với trục Ox:
1.
3
4
2
Cho hàm số y = x3 + x – 2 có đồ thị (C). Tìm tọa độ giao điểm của (C) và trục tung
(0;-2).
(1;0).
(-2;0).
(0;1).
Cho hàm số y = x4 – 4x2 – 2 có đồ thị (C) và đồ thị (P) : y = 1- x2. Số giao điểm của (P) và đồ thị (C) là
2
1
3
4
Tìm số giao điểm của đồ thị hàm số y = x4 – 2x2 và đồ thị hàm số y = x2 – 2
4
2
3
1
Tọa độ giao điểm có hoành độ nhỏ hơn 1 của đường (C): và đường thẳng (d): y = x + 1 là:
A(0;-1).
A(0;1).
A(-1;2).
A(-2;7).
Đồ thị của hàm số y = -x3 + 3x2 + 2x – 1 và đồ thị của hàm số y = 3x2 – 2x – 1 có tất cả bao nhiêu điểm chung?
1
3
2
0
Tìm giá trị của tham số m để đồ thị hàm số y = x3 – 3x + 2m đi qua điểm A(-1;6)
m = 3
m = -3
m = -2
m = 2






