30 câu hỏi
Hàm số y = f(x) liên tục trên R và có bảng biến thiên dưới đây. Khẳng định nào sau đây là đúng?
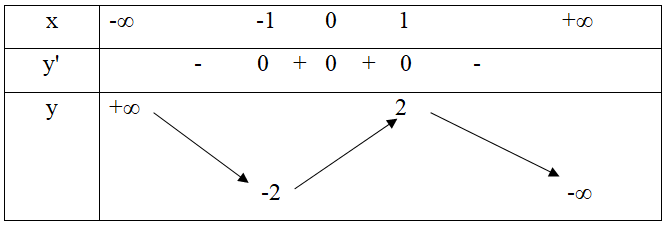
Hàm số có ba điểm cực trị
Hàm số đạt cực đại tại x = 0
Hàm số đạt cực tiểu tại x = -1
Hàm số đạt cực đại tại x = 2
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là khẳng định sai?
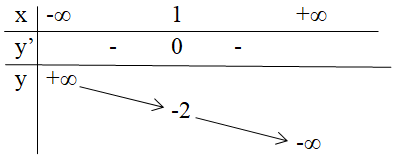
Hàm số nghịch biến trên R.
Hàm số đạt cực tiểu khi x=1.
Hàm số không có cực trị.
Hàm số y = 1/3.x3 + x2 - 2/3 có
Điểm cực đại tại x = -2, điểm cực tiểu tại x = 0
Điểm cực tiểu tại x = -2, điểm cực đại tại x = 0
Điểm cực đại tại x = -3, điểm cực tiểu tại x = 0
Điểm cực đại tại x = -2, điểm cực tiểu tại x = 2
Đồ thị hàm số y = x3 – 3x2 – 9x – 5 có điểm cực tiểu là
(3; 32).
(-1; 0).
x = -1.
x = 3
Hàm số y = 2x4 – 8x3 + 15
Nhận điểm x = 3 làm điểm cực đại.
Nhận điểm x = 0 làm điểm cực đại.
Nhận điểm x = 3 làm điểm cực tiểu.
Nhận điểm x = -3 làm điểm cực tiểu
Hàm số y = -x4 – 2x2 + 3 có bao nhiêu điểm cực trị?
1
0
3
2
Biết hàm số y = x3 – 3x + 1 có hai điểm cực trị x1; x2 Tính tổng x12 + x22.
x12 + x22 = 0
x12 + x22 = 9
x12 + x22 = 2
x12 + x22 = 1
Hàm số y = x4 – 4x2 – 5
Nhận điểm x = 3 làm điểm cực đại.
Nhận điểm x = 0 làm điểm cực đại
Nhận điểm x = 3 làm điểm cực tiểu.
Nhận điểm x = 0 làm điểm cực tiểu
Hàm số nào trong bốn hàm số được liệt kê ở bốn phướng án A, B, C, D dưới đây, không có cực trị?
y = x3 + 3x2 – 4x + 1
y = -x4 – 4x2 + 3
y = x3 – 3x + 5
![]()
Cho hàm số y = f(x) xác định, liên tục trên đoạn [-2;3] và có đồ thị là đường cong trong hình vẽ bên. Tìm số điểm cực đại của hàm số y = f(x) trên đoạn [-2; 3]
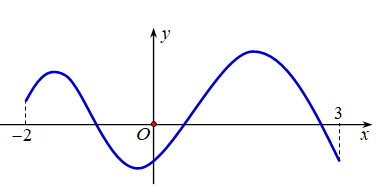
1
0
2.
3
Trong các hàm số sau, hàm số nào có hai điểm cực đại và một điểm cực tiểu?
y = x4 – x2 + 3
y = -x4 – x2 + 3
y = -x4 + x2 + 3
y = x4 + x2 + 3
Hàm số y = x3 – 3x2 – 1 đạt cực đại tại?
x = 0.
x = 2
x = -2
Không có cực trị.
Cho hàm số y = x4 – 2x2 + 2. Kết luận nào sau đây sai?
Nghịch biến (-2; 2)
Đồng biến (2; +∞)
xCT = ± 2
yCT = -2
Hàm số nào sau đây có 2 cực đại?
y = -1/2.x4 + 2x2 – 3
y = -x4 – 2x2 + 3
y = 1/4.x4 – 2x2 – 3
y = 2x4 + 2x2 – 3
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên.
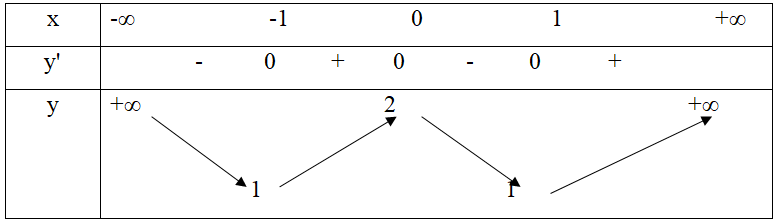
Khẳng định nào sau đây là sai?
M(0; 2) được gọi là điểm cực đại của hàm số
f(-1) được gọi là giá trị cực tiểu của hàm số
x0 = 1 được gọi là điểm cực tiểu của hàm số
Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞)
Cho hàm số y = f(x) có đồ thị là hình vẽ bên. Trong các khẳng định sau, khẳng định nào sai?
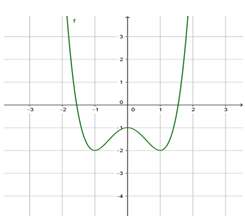
Hàm số nghịch biến trên các khoảng (-∞; -1) và (0; 1)
Tọa độ điểm cực đại của đồ thị hàm số là (-1; 0)
Hàm số đạt cực tiểu tại các điểm x = 1 và x = -1
Hàm số có ba điểm cực trị
Hàm số nào sau đây có xCĐ < xCT:
y = x3 + 3x – 1
y = x3 – 3x2 + 2x – 1
y = -x3 + 3x2 + 2
y = x4 + x2 – 1
Khẳng định nào sau đây đúng khi nói về hàm số y = x4 + 4x2 – 2?
Đạt cực tiểu tại x = 0
Có cực đại và cực tiểu
Có cực đại và không có cực tiểu
Không có cực trị.
Cho hàm số y = f(x) có đồ thị là đường cong trong hình vẽ bên. Hàm số f(x) đạt cực tiểu tại điểm nào dưới đây?
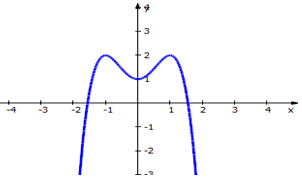
x = 1
x = -1
x = 2
x = 0
Kí hiệu m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn [1;4]. Tính giá trị biểu thức d = M – m
d = 3
d = 4
d = 5
d = 2
Hàm số có giá trị lớn nhất trên đoạn [0;3] là
1
3
2.
0
Tìm giá trị nhỏ nhất của hàm số trên đoạn [2 ;4]
min[2 ;4]y = 6
min[2 ;4]y = -2
min[2 ;4]y = -3
min[2 ;4]y = 19/3
Trên đoạn [-1; 1], hàm số y = -4/3.x3 – 2x2 – x – 3
Có giá trị nhỏ nhất tại x = -1 và giá trị lớn nhất tại x = 1
Có giá trị nhỏ nhất tại x = 1 và giá trị lớn nhất tại x = -1
Có giá trị nhỏ nhất tại x = -1 và không có giá trị lớn nhất
Không có giá trị nhỏ nhất và có giá trị lớn nhất tại x = 1
Tìm giá trị lớn nhất của hàm số trên đoạn [0; 2]
-1/3 .
-5
5
1/3
Tìm M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x3 – 3x2 – 9x + 35 trên đoạn [-4;4] là
M = 40; m = -41
M = 40; m = -8
M = -41; m = 40
M = 15; m = -8
Hàm số y = x3 – 2x2 – 7x + 5 có giá trị nhỏ nhất là m và giá trị lớn nhất là M trên đoạn [1;3]. Khi đó tổng m + M bằng
-338/27
-446/27
-10
-14/27
Tìm giá trị nhỏ nhất của hàm số trên đoạn [0;3]
min[0;3]y = 0
min[0;3]y = -3/7
min[0;3]y = -4
min[0;3]y = -1
Giá trị lớn nhất của hàm số y = x3 – 3x + 1 trên [0; 1] là:
-1
0.
2.
1.
Tìm giá trị nhỏ nhất của hàm số trên đoạn [-3;1].
mim[-3; 1]y = 3
mim[-3; 1]y = 7
mim[-3; 1]y = 2
mim[-3; 1]y = 0
Hàm số y = x3 – 3x2 + 3x + 2017
Đồng biến trên TXĐ
Nghịch biến trên tập xác định
Đồng biến trên (1; +∞)
Đồng biến trên (-5; +∞)






