30 câu hỏi
Hàm số nào sau đây đồng biến trên tập số thực R?
y = x4 – 2x2 – 5
y = - x + 1
y = x3 + 3x – 1
Trong các hàm số sau, hàm số nào luôn đồng biến trên từng khoảng xác định của nó?
(I) ; y = -x4 + x2 – 2 (II); y = x3 – 3x – 5 (III).
I và II
Chỉ I
I và III
II và III
Cho hàm số
(m khác 1)
Chọn câu trả lời đúng
Hàm số luôn giảm trên (-∞;1) và (1;+∞) với m < 1
Hàm số luôn giảm trên tập xác định.
Hàm số luôn tăng trên (-∞;1) và (1;+∞) với m > 1
Hàm số luôn tăng trên (-∞;1) và (1;+∞)
Hàm số nào trong các hàm số sau đây đồng biến trên các khoảng (-∞;2) và (2;+∞)
Hàm số nào sau đây nghịch biến trên R.
y = -x3 + 2x2 – x – 1
y = 1/3 x3 – x2 + 3x + 1
y = -1/3.x3 + x2 – x.
y = -x3 + 3x + 1
Hàm số nào sau đây đồng biến trên R.
Hàm số nào sau đây nghịch biến trên R?
y = -x3 + 3x2 + 3x – 2.
y = -x3 + 3x2 – 3x – 2
y = x3 + 3x2 + 3x – 2
y = x3 – 3x2 – 3x – 2
Hàm số nào sau đây nghịch biến trên R?
y = -x3 + 3x2 + 3x – 2
y = -x3 + 3x2 – 3x – 2.
y = x3 + 3x2 + 3x – 2
y = x3 – 3x2 – 3x – 2.
Hàm số nào sau đây đồng biến trên R?
Trong các hàm số sau, hàm số nào nghịch biến trên khoảng (-1;1)?
y = 1/x
y = x3 – 3x + 1
y = 1/x2
y = -1/x
Cho hàm số f(x) = -2x3 + 3x2 – 3x và 0 ≤ a < b. Khẳng định nào sau đây sai?
Hàm số nghịch biến trên R
f(a) > f(b).
f(b) < 0
f(a) < f(b).
Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây?
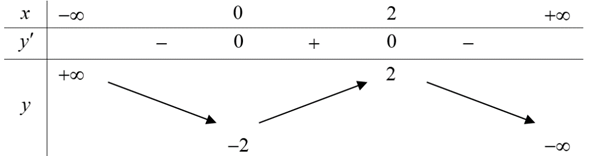
y = x3 – 3x2 – 1
y = -x3 + 3x2 – 2
y = -x3 + 3x2 – 1
y = -x3 – 3x – 2
Cho hàm số y = f(x) = x3 + 3x. Hỏi khẳng định nào sau đây là khẳng định đúng?
Hàm số f(x) đồng biến trên R
Hàm số f(x) nghịch biến trên (-1;0)
Hàm số f(x) nghịch biến trên (-∞;0).
Hàm số f(x) không đổi trên R
Đâu là hàm số đồng biến trên đoạn [2;5]?
y = x
y = x(x+1)(x+2)
y = x(x+1)(x+2)(x+3)(x+4)
Cả A, B và C đều đúng
Trong các hàm số sau, hàm số nào nghịch biến trên các khoảng xác định của chúng
Tìm tất cả các giá trị thực của tham số m đề hàm số nghịch biến trên khoảng (1;+∞)
0 < m ≤ 1
0 < m < 1
m > 1
0 ≤ m < 1
Với giá trị nào của m thì hàm số đồng biến trên khoảng (1;+∞)
m>2
m<-2
Tìm tất cả giá trị của m để hàm số đồng biến trên từng khoảng xác định
Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số là đường thẳng
song song với đường thẳng x = 1
song song với trục hoành
có hệ số góc dương.
có hệ số góc bằng -1
Đồ thị của hàm số y = x4 – x2 + 1 có bao nhiêu điểm cực trị có tung độ dương?
1
2.
3.
4
Khẳng định nào sau đây là khẳng định sai về hàm số
Hàm số đồng biến trên (1; +∞)
Hàm số đồng biến trên từng khoảng xác định.
Hàm số có cực trị
Hàm số đồng biến trên (-∞;-1)
Cho hàm số y = 2x3 + 3x2 – 12x - 12. Gọi x1, x2 lần lượt là hoành độ hai điểm cực đại và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng?
(x1 – x2)2 = 8
x1x2 = 2
x2 – x1 = 3
x12 + x22 = 6
Hỏi hàm số y = x3 – 3x2 – 9x – 2 đạt cực tiểu tại điểm nào?
x = -3
x = -1
x = 1
x = 3
Tìm tất cả các điểm cực đại của hàm số y = -x4 + 2x2 + 1
x = ±1
x = -1
x = 1
x = 0
Hàm số nào dưới đây không có cực trị?
y = x4 + x2
y = x2 - 1
y = x3 – x2
y = x3 + 3x
x = 2 không phải là điểm cực đại của hàm số nào sau đây?
Tìm tất cả các điểm cực trị của hàm số y = 1/2.sin 2x + cos x – 2017
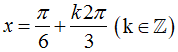
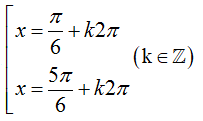
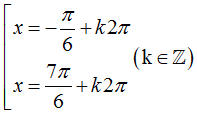
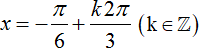
Gọi x1, x2 là hai điểm cực trị của hàm số Tính giá trị của biểu thức P = x1.x2
P = -5
P = -2
P = -1
P = -4
Cho hàm số tìm khẳng định đúng?
Hàm số đã cho có đạt cực tiểu duy nhất là y = 1
Hàm số đã cho đạt cực đại duy nhất là y = -1/2
Hàm số đã cho chỉ có giá trị cực tiểu là y = -1/2
Hàm số đã cho không có cực trị
Cho hàm số y = f(x) có đạo hàm trong khoảng (a, b) chứa điểm x0 (có thể trừ điểm x0). Tìm mệnh đề đúng trong các mệnh đề sau:
Nếu f(x) không có đạo hàm tại x0 thì f(x) không đạt cực trị tại x0
Nếu f’(x0) = 0 thì f(x) đạt cực trị tại điểm x0
Nếu f’(x0) = 0 và f’’(x0) = 0 thì f(x) không đạt cực trị tại điểm x0
Nếu f’(x0) = 0 và f’’(x0) ≠ 0 thì f(x) đạt cực trị tại điểm x0
Gợi ý cho bạn
Xem tất cả
65 câu Trắc nghiệm Ôn tập Toán 12 Chương 1 có đáp án
