25 đề thi thử Toán THPT Quốc gia có lời giải chi tiết (Đề 7)

Với a là số thực dương bất kì, mệnh đề nào sau đây đúng?

Điểm biểu diễn của các số phức $z=-2+bi$ với $b\in ℝ$ nằm trên đường thẳng có phương trình là

Giá trị lớn nhất, giá trị nhỏ nhất của hàm số$y=\sqrt{2\sin x+3}$ là

Trong không gian Oxyz, cho điểm I(1;2;-2) và mặt phẳng $\left(P\right):2x+2y+z+5=0$. Phương trình mặt cầu (S) có tâm I và cắt (P) theo một đường tròn có chu vi bằng $8\mathrm{\pi }$  là  

Gọi $z_1$ và $z_2$ là hai nghiệm phức của phương trình $z^2-2z+4=0$. Giá trị của biểu thức $\left|z_1\right|+\left|z_2\right|$ bằng

Cho $I=\underset{1}{\overset{2}{\int }}2x\sqrt{x^2-1}dx$ và đặt $u=x^2-1$. Khẳng định nào sau đây sai?

Phương trình  ${\left(\frac{1}{7}\right)}^{x^2-2x-3}=7^{x-1}$có bao nhiêu nghiệm?

Gọi M,n tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=2x^3-3x^2-12x+10$ trên đoạn [-3;3]. Biết $\frac{m}{M}=\frac{a}{b}$ là số hữu tỉ tối giản với b>0. Tổng a+b có giá trị bằng

Cho điểm M(2;1;0) và đường thẳng $\Delta :\frac{x-1}{2}=\frac{y+1}{1}=\frac{z}{-1}$. Gọi d là đường thẳng đi

qua M và vuông góc với $∆$. Vectơ chỉ phương của d là

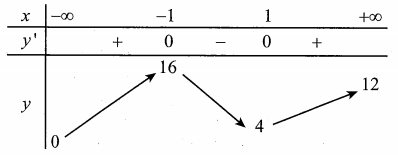
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ.

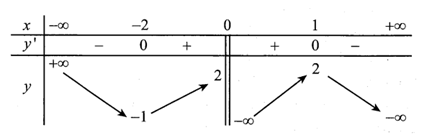
Khẳng định nào sau đây sai?

Biết $I=\underset{0}{\overset{\frac{\pi }{4}}{\int }}\left(x^2-4x+3\right)\sin \left(2x\right)dx=\frac{\pi }{c}+\frac{a}{b}$, với $a,b,c\in \mathbb{Z},\frac{a}{b}$ là phân số tối giản.

Giá trị biểu thức $P=a^b+c^{b-2a}$ là

Cho hình nón có góc ở đỉnh bằng $60°$ , bán kính đáy bằng a. Diện tích xung quanh của hình nón bằng

Trong không gian với hệ tọa độ Oxyz, cho ba điểm $A\left(-2;3;1\right),B\left(2;1;0\right),C\left(-3;-1;1\right)$. Tìm tất cả các điểm D sao cho ABCD là hình thang có đáy AD và $S_{ABCD}=3S_{\Delta ABC}$.

Cho hàm số y=f(x) liên tục trên R có đồ thị như hình vẽ.Gọi $y_1,y_2$ là cực trị của hàm số $y=f\left(x\right)-1$ Giá trị $y_1+y_2$ bằng

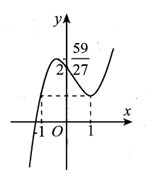
Cho dãy số $\left(u_n\right)$ với $\left\{\begin{array}{l}{u}_1=1\\ u_{n+1}=u_n+{\left(-1\right)}^{2n}\end{array}\right.$. Số hạng tổng quát  của dãy số là số hạng nào dưới đây?

Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y=x^3-3x^2+2$ là

Trong không gian Oxyz, khoảng cách từ điểm M(2;-4;-1)  tới đường thẳng $\Delta :\left\{\begin{array}{l}x=t\\ y=2-t\\ z=3+2t\end{array}\right.$ bằng

Cho hình chóp S.ABCD. Gọi M là điểm trên cạnh AB (M khác A, B), N  là điểm trên cạnh SC (N khác S, C). Giao điểm của MN và (SCD) là

Đạo hàm của hàm số $f\left(x\right)={\log }_{2}x+x^2$ là

Cho hàm số $y=x+\frac{4}{x}$. Hàm số đạt cực tiểu tại điểm

Cho hai số thực a, b đều khác 1 thỏa mãn các điều kiện  ${\log }_{\mathrm{a}}\frac{1}{2019}<{\log }_{\mathrm{a}}\frac{1}{2020}$và $b^{\frac{1}{2019}}>b^{\frac{1}{2020}}$. Phát biểu nào sau đây đúng?

Cho hình lăng trụ đứng tam giác ABCA'B'C' có đáy là $\Delta ABC$ đều cạnh a=4 và biết $S_{\Delta A^{\text{'}}BC}=8$. Thể tích khối lăng trụ là

Bất phương trình $9^x-{4.3}^{x+1}+27<0$ có tập nghiệm là khoảng $\left(a;b\right)$. Giá trị biểu thức $P=a+2b$ bằng

Cho các số dương a, b, c khác 1 thỏa mãn ${\log }_a\left(bc\right)=2,{\log }_b\left(ca\right)=4$ . Giá trị của biểu thức ${\log }_c\left(ab\right)$ là

Tập hợp điểm biểu diễn các số phức z thỏa mãn $\left|z-i\right|=\left|\overline{z}+3\right|$  trong mặt phẳng tọa độ Oxy là

Cho hàm số y=f(x) có bảng biến thiên như sau:

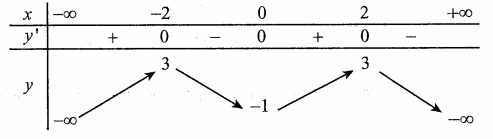
Hàm số $y=f\left(x^2-2\right)$nghịch biến trên khoảng nào dưới đây?

Trong không gian Oxyz, cho (P) là mặt phẳng đi qua M(1;4;9) và cắt các tia  tại A, B, C sao cho OA+OB+OC  đạt giá trị nhỏ nhất. Khi đó (P) đi qua điểm

Trong khai triển ${\left(x+\frac{2}{\sqrt{x}}\right)}^6$, hệ số của $x^3,\left(x>0\right)$ là

Cho hàm số $y=a{x}^4+b{x}^2+c$ có đồ thị (C), biết rằng (C) đi qua điểm A. Tiếp tuyến $∆$ tại A của đồ thị (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2. Diện tích hình phẳng giới hạn bởi , đồ thị (C) và đường thẳng x=-1;x=0 bằng

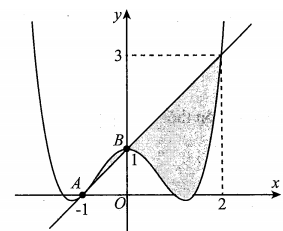
Hình chóp tứ giác đều cạnh đáy bằng a, góc giữa cạnh bên và cạnh đáy bằng $60°$. Diện tích toàn phần của hình nón ngoại tiếp hình chóp là

Cho hàm số f(x) có đạo hàm f'(x) liên tục trên đoạn [0;1] thỏa mãn $f\left(1\right)=0,\underset{0}{\overset{1}{\int }}{\left(f^{\text{'}}\left(x\right)\right)}^{2}dx=\frac{{\pi }^2}{8}$ và $\underset{0}{\overset{1}{\int }}\cos \left(\frac{\pi }{2}x\right)f\left(x\right)dx=\frac{1}{2}$ . Tích phân $\underset{0}{\overset{1}{\int }}f\left(x\right)dx$ có giá trị bằng

Cho một miếng tôn hình tròn có bán kính 50 cm. Biết hình nón có thể tích lớn nhất khi diện tích toàn phần của hình nón bằng diện tích miếng tôn ở trên. Khi đó hình nón có bán kính đáy bằng

Một người gửi tiết kiệm vào ngân hàng 200 triệu đồng theo thể thức lãi kép (tức là tiền lãi được cộng vào vốn kỳ tiếp theo). Ban đầu người đó gửi với kỳ hạn 3 tháng, lãi suất 2%/kỳ hạn, sau hai năm người đó thay đổi phương thức gửi, chuyển thành kỳ hạn một tháng với lãi suất 0,6%/tháng. Tổng số tiền lãi và gốc nhận được sau 5 năm (kết quả làm tròn tới đơn vị nghìn đồng) bằng

Tìm tất cả giá trị thực của tham số m để hàm số  $y=\frac{x^2+mx+1}{x+m}$liên tục và đạt giá trị nhỏ nhất trên  [0;2] tại một điểm $x_0\in \left(0;2\right)$

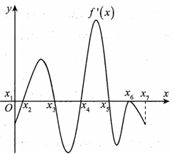
Cho hàm số y=f(x) có đồ thị f'(x) như hình vẽ bên. Biết rằng $f\left(x_1\right)+f\left(x_3\right)=f\left(x_5\right)+f\left(x_7\right)f\left(x_1\right)+f\left(x_3\right)=f\left(x_5\right)+f\left(x_7\right)$ và $f\left(x_3\right)=f\left(x_6\right)$ .Giá trị lớn nhất của hàm số y=f(x) trên $\left[x_1;x_7\right]$ bằng

Trong không gian Oxyz, tập hợp các điểm M(a;b;c) thỏa mãn bất phương trình ${\left(a-\sin \phi \right)}^2+{\left(b-\cos \phi \right)}^2+c^2\le \frac{1}{4}$ là một khối tròn xoay có thể tích bằng

Cho hai số phức $z_1,z_2$ thay đổi luôn thỏa mãn $\left|z_1-1-2i\right|=1$ và $\left|z_2-5+i\right|=2$. Giá trị nhỏ nhất của biểu thức $P=\left|z_1-z_2\right|$ bằng

Trong không gian với hệ tọa độ Oxyz, cho ba điểm $A\left(1;4;5\right),B\left(3;4;0\right),C\left(2;-1;0\right)$ và mặt phẳng $\left(P\right):3x-3y-2z-12=0$.Gọi M(a;b;c) thuộc (P) sao cho $M{A}^2+M{B}^2+3M{C}^2$ đạt giá trị nhỏ nhất. Tổng a+b+c có giá trị bằng

Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại $A,\widehat{ABC}=30°$. Tam giác SBC là tam giác đều cạnh a và mặt phẳng (SAB) vuông góc với mặt phẳng (ABC). Khoảng cách từ A đến mặt phẳng (SBC) bằng

Xét hình phẳng (H) giới hạn bởi đồ thị hàm số$f\left(x\right)=m\sin x+n\cos x$  (với $m,n\in ℝ,n>0$) trục hoành, trục tung và đường thẳng $x=\pi$ . Khi quay  quanh trục Ox thì ta được một vật thể tròn xoay có thể tích bằng  $\frac{17{\pi }^2}{2}$và $f^{\text{'}}\left(0\right)=1$. Giá trị $m+n$ bằng

Cho khối lập phương ABCD.A'B'C'D' cạnh a. Các điểm E, F lần lượt là trung điểm của C'B' và C'D' . Mặt phẳng (AEF) cắt khối lập phương đã cho thành hai phần, gọi $V_1$ là  thể tích khối chứa điểm  A và $V_2$  là thể tích khối chứa điểmC' . Tính tỉ số$\frac{V_1}{V_2}$ .

Cho hàm số $f\left(x\right)=\left|8x^4+a{x}^2+b\right|$, trong đó a, b là tham số thực. Biết rằng giá trị lớn nhất của hàm số f(x) trên đoạn [-1;1] bằng 1. Khẳng định nào sau đây là đúng?

Cho hàm số y=f(x) có bảng biến thiên như sau

Có bao nhiêu giá trị nguyên của m để phương trình ${\log }_6\left(2f\left(x\right)+m\right)={\log }_4\left(f\left(x\right)\right)$ có 2 nghiệm phân biệt?

Trong không gian Oxyz, cho điểm $A\left(1;0;2\right),B\left(-2;0;5\right),C\left(0;-1;7\right)$. Trên đường thẳng d vuông góc với mặt phẳng (ABC) tại A lấy một điểm S . Gọi H,K lần lượt là hình chiếu vuông góc của A lên SB,SC . Biết khi S di động trên  thì đường thẳng $d\left(S\ne A\right)$ luôn đi qua một điểm cố định D. Tính độ dài đoạn thẳng AD.

Có 10 học sinh ngồi vào một bàn tròn mỗi người được cầm một đồng xu và tung lên. Xác suất để không có hai người ngồi cạnh nhau cùng ra mặt sấp là

Cho hàm số y =f(x)  có đạo hàm liên tục tên đoạn [0;1] thỏa mãn $f\left(1\right)=1,\underset{0}{\overset{1}{\int }}xf\left(x\right)dx=\frac{1}{5}$và $\underset{0}{\overset{1}{\int }}{\left[f^{\text{'}}\left(x\right)\right]}^{2}dx=\frac{9}{5}$. Giá trị tích phân $I=\underset{0}{\overset{1}{\int }}f\left(x\right)dx$ là

Trong không gian Oxyz, cho hai mặt cầu $\left(S_1\right):{\left(x-1\right)}^2+y^2+z^2=4$,  $\left(S_2\right):{\left(x-2\right)}^2+{\left(y-3\right)}^2+{\left(z-1\right)}^2=1$và đường thẳng $d:\left\{\begin{array}{l}x=2-t\\ y=-3t\\ z=-2-t\end{array}\right.$ . Gọi  là hai điểm tùy ý thuộc $\left(S_1\right),\left(S_2\right)$ và M thuộc đường thẳng d. Giá trị biểu thức P=MA+MB bằng

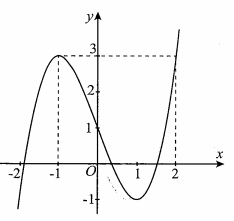
Cho hàm số y =f(x) có đạo hàm trên R và có đồ thị như hình vẽ. Đặt hàm số $y=g\left(x\right)=f\left(2x^3+x-1\right)+m$ .

Giá trị của m để $\underset{\left[0;1\right]}{\max }g\left(x\right)=-10$ là

Cho số phức z thỏa mãn $\left|z+\overline{z}+2\right|+3\left|z-\overline{z}-2i\right|\le 6$. Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của $\left|z-2-3i\right|$. Giá trị của M +5m bằng