20 CÂU HỎI
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {\left( {x - 2} \right)^2} - 1\), trục hoành và hai đường thẳng \(x = 1\), \(x = 2\) bằng
A. \(\frac{2}{3}\)
B. \(\frac{3}{2}\)
C. \(\frac{1}{3}\)
D. \(\frac{7}{3}\)
Gọi S là diện tích hình phẳng giới hạn bởi cácđường \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = - 3\),\(x = 2\)(như hình vẽ bên). Đặt \(a = \int\limits_{ - 3}^1 {f\left( x \right)dx} \),\(b = \int\limits_1^2 {f\left( x \right)dx} \).
Mệnh đề nào sau đây là đúng?
A. \(S = a + b\).
B. \(S = a - b\).
C. \(S = - a - b\).
D. \(S = b - a\).
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số \(y = \ln x\), \(y = 1\) và đường thẳng \(x = 1\) bằng
A. \({e^2}\).
B. \(e + 2\).
C. 2e.
D. \(e - 2\).
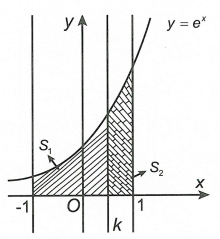
Gọi \(\left( H \right)\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = {e^x}\), trục hoành và các đường thẳng \(x = - 1\), \(x = 1\). Với \(k \in \left( { - 1;1} \right)\), đường thẳng \(x = k\) chia hình phẳng \(\left( H \right)\) thành hai hình phẳng có diện tích lần lượt là \({S_1}\) và \({S_2}\) (như hình vẽ bên). Giá trị k để \({S_1} = {S_2}\) là
A. \(2\ln 2 - 1\).
B. \(2\ln \left( {e - \frac{1}{e}} \right) - 1\).
C. \(\ln \left( {e + \frac{1}{e}} \right) - \ln 2\).
D. \(\ln 2\).
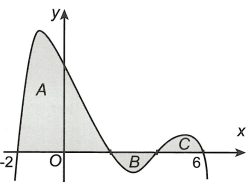
Cho hàm số \(y = f\left( x \right)\) có đồ thị trên \(\left[ { - 2;6} \right]\) như hình vẽ bên. Biết các miền A, B, \(x = 2\) có diện tích lần lượt là 32; 2; 3.
Tích phân\(\int\limits_{ - 2}^2 {\left[ {f\left( {2x + 2} \right) + 1} \right]dx} \) bằng
A. \(\frac{{45}}{2}\).
B. 41.
C. 37.
D. \(\frac{{41}}{2}\).
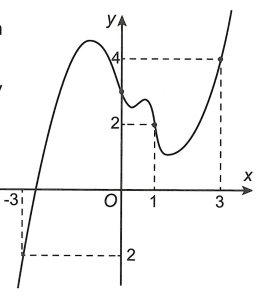
Cho hàm số \(y = f\left( x \right)\) có đồ thị của hàm số \(y = f'\left( x \right)\) như hình bên.
Đặt\(g\left( x \right) = 2f\left( x \right) - {\left( {x + 1} \right)^2}\). Mệnh đề nào dưới đây đúng?
A. \(g\left( 3 \right) > g\left( { - 3} \right) > g\left( 1 \right)\) .
B. \(g\left( { - 3} \right) > g\left( 3 \right) > g\left( 1 \right)\).
C. \(g\left( 1 \right) > g\left( { - 3} \right) > g\left( 3 \right)\).
D. \(g\left( 1 \right) > g\left( 3 \right) > g\left( { - 3} \right)\).
Gọi S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số: \(y = {x^3} - 3x\), \(y = x\). Tính S.
A. \(S = 4\).
B. \(S = 8\).
C. \(S = 2\).
D. \(S = 0\).
Gọi S là diện tích hình phẳng giới hạn bởi các đường \(my = {x^2}\), \(mx = {y^2}\)(với \(m > 0\)). Tìm giá trị của m để \(S = 3\).
A. \(m = 1\).
B. \(m = 2\).
C. \(m = 3\).
D. \(m = 4\).
Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm \(y = {x^2}\)và \(y = \frac{{2x}}{{x - 1}}\)là \(S = a + b\ln 2\)với a, b là những số hữu tỷ. Giá trị của \(a + b\) là
A. \( - \frac{1}{3}\).
B.2.
C. \( - \frac{2}{3}\).
D.1.
Cho \(\left( H \right)\) là hình phẳng giới hạn bởi parabol \(y = \sqrt 3 {x^2}\), cung tròn có phương trình \(y = \sqrt {4 - {x^2}} \)(với \(0 \le x \le 2\)) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của \(\left( H \right)\) là
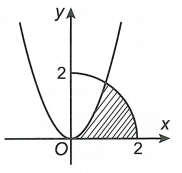
A. \(\frac{{4\pi + \sqrt 3 }}{{12}}\).
B. \(\frac{{4\pi - \sqrt 3 }}{6}\)
C. \(\frac{{4\pi + 2\sqrt 3 - 3}}{6}\).
D. \(\frac{{5\sqrt 3 - 2\pi }}{3}\).
Hình phẳng \(\left( H \right)\) được giới hạn bởi đồ thị \(\left( C \right)\)của hàm đa thức bậc ba và parabol \(\left( P \right)\) có trục đối xứng vuông góc với trục hoành. Phần tô đậm của hình vẽ có diện tích bằng
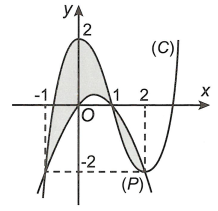
A. \(\frac{{37}}{{12}}\).
B. \(\frac{7}{{12}}\).
C. \(\frac{{11}}{{12}}\).
D. \(\frac{5}{{12}}\).
Tính thể tích V của vật thể nằm giữa hai mặt phẳng \(x = 0\) và \(x = \frac{\pi }{4}\), biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x \(\left( {0 \le x \le \frac{\pi }{4}} \right)\) làm một tam giác đều có cạnh là \(2\sqrt {\cos 2x} \).
A. \(V = \sqrt 3 \).
B. \(V = \frac{{\sqrt 3 }}{2}\).
C. \(V = \frac{1}{2}\).
D. \(V = \frac{{\sqrt 2 }}{2}\).
Cho hình phẳng \(\left( H \right)\) giới hạn bởi các đường \(y = {x^2} + 2\), \(y = 0\), \(x = 1\), \(x = 2\). Gọi V lả thể tích của khối tròn xoay được tạo thành khi quay \(\left( H \right)\) xung quanh trục Ox. Mệnh đề nào dưới đây đúng?
A. \(V = \int\limits_1^2 {\left( {{x^2} + 2} \right)dx} \).
B. \(V = \int\limits_1^2 {{{\left( {{x^2} + 2} \right)}^2}dx} \).
C. \(V = \pi \int\limits_1^2 {{{\left( {{x^2} + 2} \right)}^2}dx} \).
D. \(V = \pi \int\limits_1^2 {\left( {{x^2} + 2} \right)dx} \).
Cho hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị hàm số \(y = \frac{{\sqrt {2x - 1} }}{{2x + 1}}\), trục hoành, hai đường thẳng \(x = 1\), \(x = 2\). Thể tích cảu vật thể tròn xoay tạo thành khi cho hình \(\left( H \right)\) quay xung quanh trục Ox bằng \(V = \pi \left( {\ln \frac{{\sqrt a }}{3} + b} \right)\), trong đó a, b là các số hữu tỷ. Khi đó tích a.b bằng
A. \(\frac{{10}}{3}\).
B. \( - \frac{{10}}{3}\).
C. 2.
D. –2.
Cho parabol \(\left( P \right)\): \(y = 16 - {x^2}\) và hai điểm \(A\left( {a;0} \right)\), \(B\left( { - a;0} \right)\); \(a < 0 < 4\). Gọi \(\left( H \right)\) là hình phẳng giới hạn bởi \(\left( P \right)\) và trục Ox, \(\left( {{H_1}} \right)\) là hình chữ nhật ABCD với C, D là hai điểm thuộc \(\left( P \right)\). Gọi V là thể tích hình tròn xoay có được khi xoay \(\left( H \right)\) quanh Oy và \({V_1}\) là thể tích hình tròn xoay có được khi xoay \(\left( {{H_1}} \right)\) quanh Oy. Giá trị lớn nhất của tỉ số \(\frac{{{V_1}}}{V}\) bằng
A. \(\frac{2}{3}\).
B. \(\frac{1}{4}\).
C. \(\frac{1}{2}\).
D. \(\frac{3}{4}\).
Kí-hiệu \(\left( H \right)\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = 2\left( {x - 1} \right){e^x}\), trục tung và trục hoành. Tính thể tích V của khối tròn xoay thu được khi quay hình \(\left( H \right)\) xung quanh trục Ox:
A. \(V = 4 - 2e\).
B. \(V = \left( {4 - 2e} \right)\pi \).
C. \(V = {e^2} - 5\).
D. \(V = \left( {{e^2} - 5} \right)\pi \).
Cho hình phẳng \(\left( H \right)\) giới hạn bởi hai đồ thị \(\left( {{C_1}} \right)\): \(y = 2{x^2}\) và \(\left( {{C_2}} \right)\): \({y^2} = 4x\). Quay hình phẳng \(\left( H \right)\) xung quanh trục Ox ta thu được khối tròn xoay có thể tích là
A. \(V = \frac{{88\pi }}{5}\).
B. \(V = \frac{{9\pi }}{{70}}\).
C. \(V = \frac{{4\pi }}{3}\).
D. \(V = \frac{{6\pi }}{5}\).
Cho hình phẳng \(\left( H \right)\) giới hạn bởi các đường \(\left( {{C_1}} \right)\): \(f\left( x \right) = x - \pi \), \(\left( {{C_2}} \right)\): \(g\left( x \right) = \sin x\) và \(x = 0\). Gọi V là thể tích khối tròn xoay tạo thành do \(\left( H \right)\) quay quanh trục hoành và \(V = p{\pi ^2}\), \(p \in \left( \mathbb{Q} \right)\). Giá trị của 24p bằng
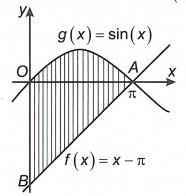
A. 8.
B. 4.
C. 24.
D. 12.
Để chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên. Biết rằng \(OO' = 5\,cm\), \(OA = 10\,cm\), \(OB = 20\,cm\), đường cong AB là một phần của parabol có đỉnh là điểm A. Thể tích của chiếc mũ bằng
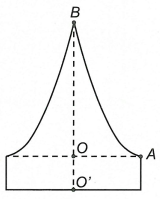
A. \(\frac{{2750\pi }}{3}c{m^3}\).
B. \(\frac{{2500\pi }}{3}c{m^3}\).
C. \(\frac{{2050\pi }}{3}c{m^3}\).
D. \(\frac{{2250\pi }}{3}c{m^3}\).
Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = \sqrt x \), \(y = 0\) và \(x = 4\) quanh trục Ox. Đường thẳng \(x = a\)\(\left( {0 < a < 4} \right)\) cắt đồ thị hàm số \(y = \sqrt x \) tại M như hình vẽ bên dưới:

Gọi \({V_1}\) là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng \(V = 2{V_1}\). Khi đó
A. \(a = 2\).
B. \(a = 2\sqrt 2 \).
C. \(a = \frac{5}{2}\).
D. \(a = 3\).

