12 CÂU HỎI
Trong không gian với hệ toạ độ Oxyz, phương trình nào sau đây là phương trình tham số của đường thẳng?
A. \(\left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y = - 3 + 4t}\\{z = 5 - 7t}\end{array}} \right.\)
B. \(\left\{ {\begin{array}{*{20}{l}}{x = 3 + {t^2}}\\{y = 2 + 9t}\\{z = - 6 + 11t}\end{array}} \right.\)
C. \(\left\{ {\begin{array}{*{20}{l}}{x = 9 + 17t}\\{y = 8 + 2t}\\{z = - 12 + {t^2}}\end{array}} \right.\)
D. \(\left\{ {\begin{array}{*{20}{l}}{x = 15 + t}\\{y = 25 + \sqrt t }\\{z = 35 - t}\end{array}} \right.\)
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }.\) Cặp vectơ nào sau đây là cặp vectơ chỉ phương của mặt phẳng \(({\rm{ABCD}})\) ?
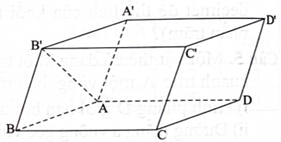
A. \(\overrightarrow {{\rm{AB}}} ,\overrightarrow {{\rm{AA}}} .\)
B. \(\overrightarrow {{\rm{AB}}} ,\overrightarrow {{\rm{A}}{{\rm{B}}^\prime }} \)
C. \(\overrightarrow {{\rm{AB}}} ,\overrightarrow {{{\rm{A}}^\prime }{\rm{B}}} .\)
D. \(\overrightarrow {{\rm{AD}}} ,\overrightarrow {{{\rm{A}}^\prime }{{\rm{B}}^\prime }} .\)
Cho hàm số \({\rm{f}}({\rm{x}})\) có đồ thị như hình bên. Biết rằng một trong bốn đường thẳng sau đây là đường tiệm cận xiên của đồ thị hàm số, đường đó là đường nào?
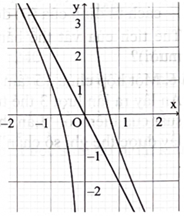
A. \(y = 2x.\)
B. \({\rm{y}} = \frac{{ - {\rm{x}}}}{2}.\)
C. \(y = - 2x.\)
D. \({\rm{y}} = \frac{{\rm{x}}}{2}.\)
Cho hàm số \({\rm{f}}({\rm{x}})\) có đồ thị như hình bên. Biết rằng một trong bốn điểm sau đây là tâm đối xứng của đồ thị hàm số, điểm đó là điểm nào?
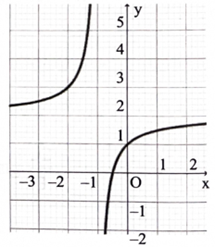
A. \({\rm{M}}(0;1).\)
B. \({\rm{N}}( - 1;2).\)
C. \({\rm{P}}( - 2;3).\)
D. \({\rm{Q}}(0;3).\)
Phát biểu nào sau đây là đúng với \({\rm{f}}({\rm{x}})\) là hàm số bất kì liên tục trên \(\mathbb{R}\) ?
A. \(\int_0^2 f (x)dx = \int_1^0 f (x)dx + \int_1^2 f (x)dx.\)
B. \(\int_0^2 f (x)dx = \int_0^1 f (x)dx + \int_2^1 f (x)dx.\)
C. \(\int_0^2 f (x)dx = \int_1^0 f (x)dx + \int_2^1 f (x)dx.\)
D. \(\int_0^2 f (x)dx = \int_0^1 f (x)dx + \int_1^2 f (x)dx.\)
Trong không gian với hệ tọa độ Oxyz, khoảng cách từ điểm \({\rm{M}}(9;7;8)\) đến mặt phẳng \(({\rm{P}}):{\rm{ax}} + {\rm{by}} + {\rm{cz}} + {\rm{d}} = 0\) bằng
A. \(\frac{{|7{\rm{a}} + 8\;{\rm{b}} + 9{\rm{c}} + {\rm{d}}|}}{{\sqrt {{{\rm{a}}^2} + {{\rm{b}}^2} + {{\rm{c}}^2}} }}.\)
B. \(\frac{{|9{\rm{a}} + 7\;{\rm{b}} + 8{\rm{c}} + {\rm{d}}|}}{{\sqrt {{{\rm{a}}^2} + {{\rm{b}}^2} + {{\rm{c}}^2}} }}.\)
C. \(\frac{{|7{\rm{a}} + 8\;{\rm{b}} + 9{\rm{c}} + {\rm{d}}|}}{{\sqrt {{7^2} + {8^2} + {9^2}} }}.\)
D. \(\frac{{|9a + 7b + 8c + d|}}{{\sqrt {{9^2} + {7^2} + {8^2}} }}.\)
Trong không gian với hệ toạ độ Oxyz, vectơ nào sau đây là một vectơ pháp tuyến của mặt \({\rm{y}} - 2{\rm{x}} - 5{\rm{z}} + 8 = 0.\)
A. \(\overrightarrow {{n_1}} = (1;2;5).\)
B. \(\overrightarrow {{{\rm{n}}_2}} = (1; - 2; - 5).\)
C. \(\overrightarrow {{n_3}} = ( - 2;1; - 5).\)
D. \(\overrightarrow {{{\rm{n}}_4}} = (2;1;5).\)
Trong không gian với hệ tọa độ Oxyz mặt cầu \({({\rm{x}} + 13)^2} + {({\rm{y}} - 14)^2} + {({\rm{z}} - 15)^2} = {4^2}\) có bán kính bằng
A. 16.
B. 2.
C. 256.
D. 4.
Hàm số nào sau đây là một nguyên hàm của hàm số \({\rm{f}}({\rm{x}}) = \frac{1}{{{{\sin }^2}{\rm{x}}}}\) ?
A. \({F_1}(x) = \tan x + C.\)
B. \({F_2}(x) = - \tan x + C.\)
C. \({F_3}(x) = - \cot x.\)
D. \({{\rm{F}}_4}({\rm{x}}) = \cot {\rm{x}}.\)
Trong mặt phẳng với hệ tọa độ Oxy, nếu hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) liên tục và nhận giá trị dương trên đoạn [1; 2] thì diện tích hình phẳng giới hạn bởi đồ thị hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) và các đường thẳng \({\rm{y}} = 0,{\rm{x}} = 1,{\rm{x}} = 2\) bằng
A. \(\int_2^1 | f(x)|dx.\)
B. \(\int_1^2 f (x)dx.\)
C. \(\pi \int_1^2 {({\rm{f}}(} {\rm{x}}){)^2}{\rm{dx}}.\)
D. \(\pi \int_2^1 {({\rm{f}}(} {\rm{x}}){)^2}{\rm{dx}}.\)
Nếu các biến cố \({\rm{A}},{\rm{B}}\) thoả mãn \({\rm{P}}({\rm{A}}) > 0,{\rm{P}}({\rm{B}}) > 0\) thì biểu thức \({\rm{P}}({\rm{B}}\mid {\rm{A}})\) bằng
A. \(\frac{{{\rm{P}}({\rm{A}}\mid {\rm{B}}) \cdot {\rm{P}}({\rm{B}})}}{{{\rm{P}}({\rm{A}})}}.\)
B. \(\frac{{{\rm{P}}({\rm{A}}\mid {\rm{B}}) \cdot {\rm{P}}({\rm{A}})}}{{{\rm{P}}({\rm{B}})}}.\)
C. \(\frac{{{\rm{P}}({\rm{A}}\mid {\rm{B}})}}{{{\rm{P}}({\rm{B}})}}.\)
D. \(\frac{{{\rm{P}}({\rm{A}}\mid {\rm{B}})}}{{{\rm{P}}({\rm{A}})}}.\)
Nếu một mẫu số liệu có phương sai bằng 0,09 thì có độ lệch chuẩn bằng
A. 0,09.
B. 0,045.
C. 0,3.
D. 0,0081.
Gợi ý cho bạn
Đề luyện thi số 03 - copy
Bài tập số 1
Đề luyện thi số 03
Đề luyện thi số 03
