50 CÂU HỎI
Với các số thực dương a, b bất kì, giá trị của bằng
A.
B.
C.
D.
Phương trình có nghiệm là
A. x = 1
B. x = 5
C. x = 4
D. x = 8
Trong không gian với hệ trục tọa độ Oxyz, cho hai vectơ và . Khi đó bằng
A. (-3;4;2)
B. 0
C. -2
D. -6
Cho khối lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a và AA' = 2a. Thể tích của khối lăng trụ đã cho bằng:
A.
B.
C.
D.
Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới. Số nghiệm của phương trình 2f(x) - 3 = 0 là
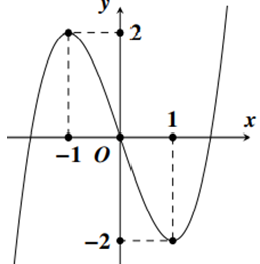
A. 3
B. 2
C. 0
D. 1
Họ nguyên hàm của hàm số là
A.
B.
C.
D.
Đồ thị của hàm số có tiệm cận ngang là
A. x = 2
B. y = -3
C. x = -3
D. y = 2
Cho hình nón có bán kính đáy R = 5 và đường sinh l = 12. Diện tích xung quanh của hình nón đã cho bằng
A.
B.
C.
D.
Cho khối chóp có diện tích mặt đáy là a3 và chiều cao bằng 3a. Thể tích của khối chóp bằng
A.
B.
C.
D.
Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau
 Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. (-3;0)
B.
C. (0;2)
D.
Cho hàm số f(x) có bảng biến thiên như sau:
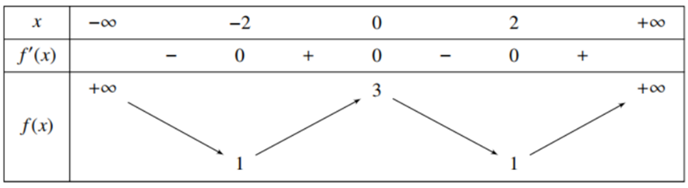 Số điểm cực trị của hàm số đã cho là
Số điểm cực trị của hàm số đã cho là
A. 2
B. 0
C. 1
D. 3
Cho Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;-2;4), B(3;0;-2). Tọa độ trung điểm M của đoạn AB là
A.
B.
C.
D.
Hàm số có tập xác định là
A.
B.
C.
D.
Cho khối lăng trụ có đáy là hình vuông cạnh a và thể tích bằng 3a3. Chiều cao khối lăng trụ bằng.
A. 2a
B. a
C.
D. 3a
Hàm số nào dưới đây có đồ thị như trong hình bên?
A.
B.
C.
D.
So sánh các số a, b, c biết x > 1 và a, b, c là các số dương khác 1 và thỏa mãn bất đẳng thức
A. c > b > a
B. c > a > b
C. a > b > c
D. b > a > c
Hàm số nào dưới đây có bảng biến thiên như sau?
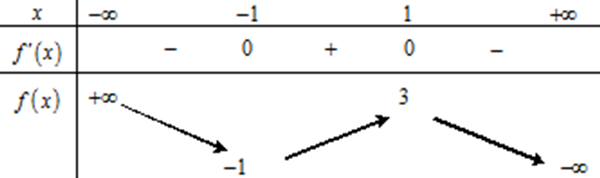
A.
B.
C.
D.
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi O, O' lần lượt là tâm của hình vuông ABCD và A'B'C'D'. Khi quay hình lập phương ABCD.A'B'C'D' xung quanh OO' được một hình tròn xoay có diện tích xung quanh bằng
A.
B.
C.
D.
Giá trị nhỏ nhất của hàm số f(x) = x3 - 3x + 1 trên đoạn [-2;0] bằng
A. -1
B. -2
C. 3
D. 1
Cho khối lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh 2a và góc giữa đường thẳng CB' và mặt phẳng (ABC) bằng 45o. Thể tích của khối lăng trụ đã cho bằng
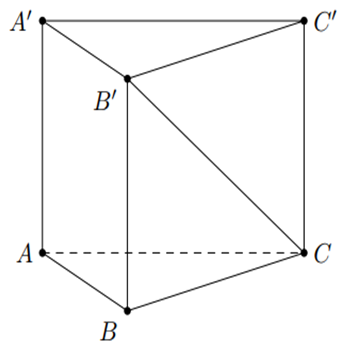
A.
B.
C.
D.
Nghiệm của phương trình là
A.
B.
C.
D. x = 2
Họ nguyên hàm của hàm số là
A.
B.
C.
D.
Trong không gian Oxyz, cho ba điểm A(3;2;-1), B(-1;-x;1), C(7;-1;y). Khi A. B. C thẳng hàng, giá trị x + y bằng
A. -8
B. -4
C. -5
D. -1
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
A. 2
B. 4
C. 1
D. 3
Một người gửi ngân hàng 18 triệu đồng theo hình thức lãi kép kì hạn 1 năm với lãi suất 8%/năm. Hỏi sau 7 năm người đó có bao nhiêu tiền? (đơn vị: triệu đồng, kết quả làm tròn đến hàng phần trăm)
A. 31,17
B. 30,85
C. 31,45
D. 31, 34
bằng
A.
B.
C.
D.
Cho hình trụ có hai đáy là hình tròn (O) và (O'), bán kính đáy bằng R và chiều cao bằng 2R. Một hình nón có đỉnh O' và đáy là hình tròn (O;R). Tỉ số diện tích toàn phần của hình trụ và hình nón bằng
A. 2
B.
C.
D.
Cho hình chóp S.ABC có , SA = 2a, đáy ABC là tam giác đều cạnh a. Gọi M, N lần lượt là trung điểm các cạnh bên SA, SB. Thể tích khối đa diện MNABC bằng
A.
B.
C.
D.
Cho hàm số có đồ thị như hình. Số điểm cực trị của hàm số là
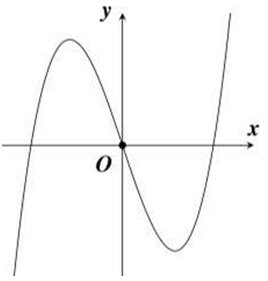
A. 2
B. 3
C. 5
D. 4
Cho hàm số f(x) có đạo hàm . Số điểm cực trị của hàm số đã cho là
A. 1
B. 3
C. 4
D. 2
Hàm số đồng biến trên khoảng
A. (2;4)
B. (0;4)
C. (0;2)
D.
Đạo hàm của hàm số là
A.
B.
C.
D.
Trong không gian Oxyz cho mặt cầu (S) có tâm I(1;2;-2) có diện tích Phương trình của mặt cầu (S) là
A.
B.
C.
D.
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông và SA vuông góc với mặt phẳng (ABCD). Biết tam giác SBD đều và có diện tích bằng Góc giữa hai mặt phẳng (SCD) và (ABCD) bằng
A. 45o
B. 60o
C. 90o
D. 75o
Cho các số thõa mãn Giá trị của bằng
A.
B.
C.
D.
Có bao nhiêu giá trị của tham số m để phương trình có hai nghiệm phân biệt thỏa mãn ?
A. 0
B. 1
C. 2
D. 3
Có bao nhiêu giá trị nguyên của tham số m để ?
A. 5
B. 6
C. 8
D. 3
Cho hình chóp tứ giác đều S.ABCD có góc giữa hai mặt phẳng (SAB) và (SCD) bằng 60o và khoảng cách giữa hai đường thẳng SA và CD bằng a. Tính thể tích V của khối chóp S.ABCD theo a.
A.
B.
C.
D.
Tập tất cả các giá trị của tham số m để bất phương trình nghiệm đúng với mọi là
A. (0;1)
B. [0;1]
C. (-2;0)
D. [-2;0]
Đồ thị hàm số y = f(x) đối xứng với đồ thị của hàm số y = 2022x qua điểm I(1;1). Giá trị của biểu thức bằng
A. -2021
B. -2023
C. -2020
D. 2020
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Tam giác SAB là tam giác vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Tâm mặt cầu ngoại tiếp hình chóp S.ABC là
A. điểm O
B. trung điểm của SC
C. trung điểm của AB
D. trung điểm của SD
Họ nguyên hàm bằng
A.
B.
C.
D.
Có bao nhiêu giá trị nguyên của tham số m để hàm số đạt giá trị nhỏ nhất tại x = 0?
A. 6
B. 4
C. 3
D. 5
Cho tam giác ABC vuông tại A và AD là đường cao. Biết AB = logy, AC = log 3, AD = logx, BC = log9. Tính
A.
B. 3
C.
D. 1
Cho khối nón có thiết diện qua trục là tam giác SAB vuông tại S. Biết tam giác SAB có bán kính đường tròn nội tiếp bằng . Tính thể tích khối nón đã cho
A.
B.
C.
D.
Cho hàm số (C). Có bao nhiêu giá trị nguyên của tham số để đường thẳng y = 2x + m cắt (C) tại hai điểm phân biệt A, B sao cho góc nhọn?
A. 6
B. 7
C. 4
D. 5
Có bao nhiêu giá trị nguyên của m để phương trình có 5 nghiệm phân biệt?
A. 7
B. 3
C. 1
D. 5
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Một mặt phẳng thay đổi, vuông góc với SO và cắt SO, SA, SB, SC, SD lần lượt tại I, M, N, P, Q. Một hình trụ có một đáy là đường tròn ngoại tiếp tứ giác (MNPQ) và một đáy nằm trên mặt phẳng (ABCD). Thể tích khối trụ lớn nhất bằng
A.
B.
C.
D.
Gọi a là số thực lớn nhất để bất phương trình nghiệm đúng với mọi . Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, mặt bên SAB là tam giác đều, . Thể tích khối chóp S.ABCD bằng
A.
B.
C.
D.

